
- •2008 Содержание
- •5.8 Нечеткие высказывания и нечеткие выводы… 112
- •6. Построение нечетких систем в диалоговом режиме с помощью Fuzzy Logic Toolbox ……….130
- •1 Обоснование теории нечетких множеств
- •1.1 Введение
- •1.2 Анализ видов неопределенности информации, характерных для процесса управления сложными системами
- •1.3 Человеко-машинные системы
- •1.4 Нечеткие системы
- •1.5 Возможности применения теории нечетких множеств и интервального анализа для описания различных видов неопределенности
- •2. Теория нечетких множеств
- •2.1. Четкие множества
- •2.2 Операции над четкими множествами
- •2.3 Декартово произведение множеств
- •3. Нечеткие множества
- •3.1 Понятие нечеткого множества
- •3.2 Некоторые характеристики нечетких множеств
- •3.3 Нечеткая и лингвистическая переменные
- •3.4 О методах построения функций принадлежности нечетких множеств
- •3.5 Операции над нечеткими множествами
- •4 Нечеткие числа
- •4.1 Понятие нечеткого числа
- •4.2 Операции над нечеткими числами
- •4.3 Нечеткие отношения
- •4.4 Свойства нечетких отношений
- •5 Основы математической логики
- •5.1 Алгебра высказываний
- •5.2 Булевы функции
- •5.3 Логика предикатов
- •5.4 Равносильные формулы логики предикатов
- •1) И ;
- •2) И ;
- •3) И ;
- •4) И .
- •5.5 Нечеткая логика
- •5.6 Нечеткие логические формулы и их свойства
- •5.7 Нечеткие предикаты и кванторы
- •5.8 Нечеткие высказывания и нечеткие выводы
- •5.9 Промышленные применения
- •6. Построение нечетких систем в
- •Диалоговом режиме с помощью
- •Fuzzy Logic Toolbox
- •1. Алгебра высказываний.
2.2 Операции над четкими множествами
Теперь
рассмотрим некоторые операции над
множествами. Прежде рассмотрим отношение
вложения множеств. Вводится
понятие подмножества. Если элементы
множества ![]() являются в тоже время элементами
множества
являются в тоже время элементами
множества ![]() ,
то говорят, что
,
то говорят, что ![]() является подмножеством
является подмножеством ![]() ,
что обозначается как
,
что обозначается как
![]() .
.
Значок
![]() употребляется в случае, если не исключена
возможность совпадения множеств
употребляется в случае, если не исключена
возможность совпадения множеств ![]() и
и ![]() .
Если такая возможность исключена, то
употребляется значок
.
Если такая возможность исключена, то
употребляется значок ![]() ,
а множество
,
а множество ![]() называется собственным подмножеством
называется собственным подмножеством
![]() .
Все
множество
.
Все
множество ![]() и пустое множество
и пустое множество ![]() называются несобственными подмножествами.
Множества
называются несобственными подмножествами.
Множества ![]() и
и ![]() будут равными, если одновременно
выполняются условия
будут равными, если одновременно
выполняются условия
![]() и
и
![]() .
.
Если определить отношение вложения через характеристические функции, то получим следующее неравенство
![]() ,
для
,
для ![]() .
(2.12)
.
(2.12)
Суммой
(объединением) множеств ![]() и
и ![]() называется множество, состоящее из
элементов, принадлежащих хотя бы одному
множеству. Другими словами, элементы
принадлежащие одновременно
называется множество, состоящее из
элементов, принадлежащих хотя бы одному
множеству. Другими словами, элементы
принадлежащие одновременно ![]() и
и ![]() ,
входят в сумму только один раз. Отсюда
следует, что
,
входят в сумму только один раз. Отсюда
следует, что
![]()
где
![]() - знак суммы. Можно определить сумму
любого числа множеств
- знак суммы. Можно определить сумму
любого числа множеств
![]() .
.
Геометрически (диаграмма Венна) сумму двух множеств можно представить в виде заштрихованной области на рис.1.
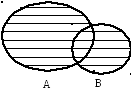
Рис.1
С помощью характеристических функций операцию объединения можно представить следующим образом (алгебраическая форма)
![]() ,
для
,
для
![]() (2.13)
(2.13)
В результате получим четыре класса элементов:
![]() -
элементы, не входящие ни в множество
-
элементы, не входящие ни в множество ![]() ,
ни в множество
,
ни в множество ![]() ;
;
![]() -
элементы, принадлежащие только множеству
-
элементы, принадлежащие только множеству
![]() и не принадлежащие множеству
и не принадлежащие множеству ![]() ;
;
![]() -
элементы, принадлежащие только множеству
-
элементы, принадлежащие только множеству![]() и не принадлежащие множеству
и не принадлежащие множеству ![]() ;
;
![]() -
элементы, принадлежащие одновременно
множествам
-
элементы, принадлежащие одновременно
множествам ![]() и
и ![]() .
.
Логически
операцию объединения двух множеств
можно охарактеризовать словами: элемент
![]() принадлежит
множеству
принадлежит
множеству
![]() или
множеству
или
множеству
![]() .
При этом связка или
одновременно
означает и связку и.
Поэтому то, что элемент
.
При этом связка или
одновременно
означает и связку и.
Поэтому то, что элемент ![]() принадлежит
множеству
принадлежит
множеству
![]() или/и
множеству
или/и
множеству
![]() ,
выражается формулой
,
выражается формулой
![]() ,
(2.14)
,
(2.14)
где
![]() - символ логической связки или,
которая называется дизъюнкцией.
- символ логической связки или,
которая называется дизъюнкцией.
С
точки зрения логики, вместо одной
предметной
переменной ![]() удобно ввести две логичиские переменные:
характеристические функции
удобно ввести две логичиские переменные:
характеристические функции ![]() и
и ![]() ,
которые принимают только два логических
значения: 1 для истинного
значения
и 0 для ложного.
,
которые принимают только два логических
значения: 1 для истинного
значения
и 0 для ложного.
Допустим,
что элемент ![]() принадлежит классу
принадлежит классу ![]() ,
то значения логических переменных
будут:
,
то значения логических переменных
будут: ![]() и
и ![]() .
Пусть теперь элемент
.
Пусть теперь элемент ![]() принадлежит классу
принадлежит классу ![]() ,
то логические переменные примут значения:
,
то логические переменные примут значения:
![]() и
и ![]() .
Существуют еще два варианта, когда
элемент принадлежит либо классу
.
Существуют еще два варианта, когда
элемент принадлежит либо классу ![]() ,
либо классу
,
либо классу ![]() .
.
Переменные
![]() и
и ![]() в это случае определяют некоторую
логическую функцию:
в это случае определяют некоторую
логическую функцию:
![]() ,
(2.15)
,
(2.15)
которая,
в случае дизъюнкции, записывается как
![]() .
При использовании в качестве логических
переменных характеристические функции
.
При использовании в качестве логических
переменных характеристические функции
![]() и
и ![]() символ логической связки или
имеет смысл взятия максимума, то есть
значение логической функции
символ логической связки или
имеет смысл взятия максимума, то есть
значение логической функции ![]() равно максимальному значению
характеристических функций для данного
элемента
равно максимальному значению
характеристических функций для данного
элемента ![]() .
.
Удобно построить таблицу истинности
Таблица 1. Таблица истинности
-
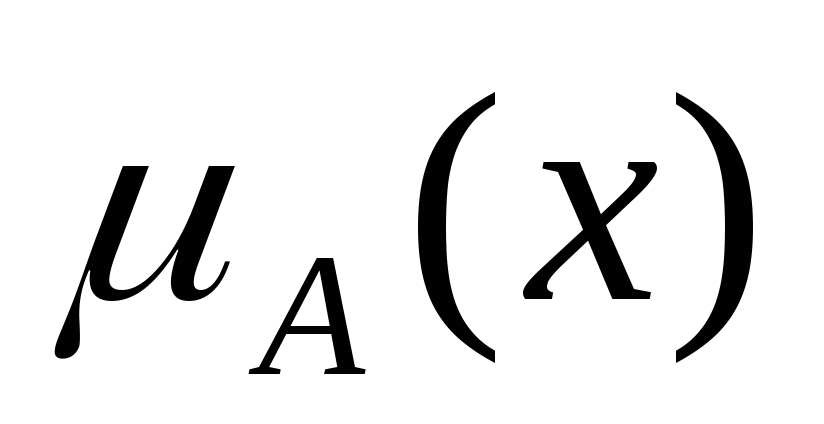

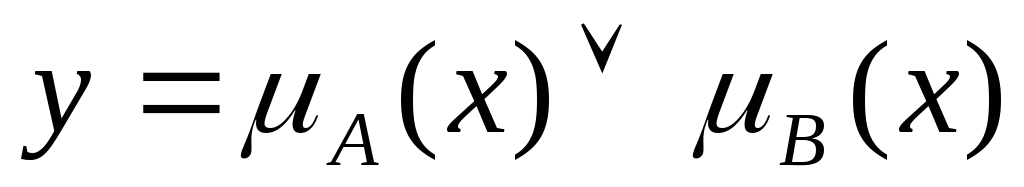 .
.0
0
0
1
0
1
0
1
1
1
1
1
Из
таблицы истинности легко усмотреть,
что четыре комбинации логических
переменных ![]() и
и ![]() отвечают четырем классам
отвечают четырем классам ![]()
Пересечением
или общей частью множеств ![]() и
и
![]() является множество, состоящее из
элементов, которые одновременно
принадлежат как множеству
является множество, состоящее из
элементов, которые одновременно
принадлежат как множеству ![]() так и множеству
так и множеству ![]() .
Пересечение, обозначаемое следующим
образом,
.
Пересечение, обозначаемое следующим
образом,
![]()
схематически представлено на рис.2 заштрихованной областью.
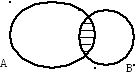
Рис. 2
Через характеристические функции операция пересечесния запишется следующим образом (алгебраичекая форма)
![]() ,
для
,
для
![]() (2.16)
(2.16)
С
точки зрения логики, это означает, что
элемент
![]() одновременно принадлежит множествам
одновременно принадлежит множествам
![]() и
и
![]() можно представить выражением
можно представить выражением
![]() .
(2.17)
.
(2.17)
Здесь
![]() - символ логической связки и,
которая называется конъюнкцией.
- символ логической связки и,
которая называется конъюнкцией.
При
использовании в качестве логических
переменных характеристические функции
![]() и
и ![]() символ логической связки и
имеет смысл взятия минимума, то есть
значение логической функции
символ логической связки и
имеет смысл взятия минимума, то есть
значение логической функции ![]() равно минимальному значению
характеристических функций для данного
элемента
равно минимальному значению
характеристических функций для данного
элемента ![]() .
.
Таблица истинности в случае конъюнкции имеет вид
Таблица 2.
Таблица истинности для конъюнкции
-


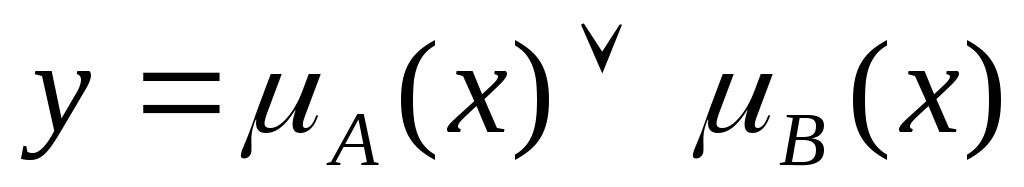 .
.0
0
0
1
0
0
0
1
0
1
1
1
Если в таблице истинности для конъюнкции все нули заменить единицами, а все единицы – нулями, то получим таблицу для дизъюнкции. Этот факт определяет взаимную двойственность конъюнкции и дизъюнкции. Для любой логической операции можно найти двойственную, о чем будет сказанно в дальнейшим.
Стрелка
Пирса, штрих Шеффера и разность. Рассмотрим
две новые операции – стрелка Пирса и
штрих Шиффера на конкретном примере.
Пусть задано фундаментальное множество
![]() и два подмножества
и два подмножества ![]() и
и ![]() .
Тогда операция – стрелка Пирса на этих
множествах выглядит следующим образом
.
Тогда операция – стрелка Пирса на этих
множествах выглядит следующим образом
![]() .
.
Отсюда следует, что в результате применения операции стрелки Пирса к двум подмножествам фундаментального множества получаем множество, которое является дополнением объединения подмножеств до фундаментального множества.
Операция штрих Шиффера выглядит следующим образом
![]()
В результате операции штриха Шиффера получаем множество, которое дополняет пересечение подмножеств до фундаментального множества.
Разностью
множеств ![]() и
и ![]() называется множество, содержащее все
элементы множества
называется множество, содержащее все
элементы множества ![]() ,
не входящие в множество
,
не входящие в множество ![]() ,
и не содержащее никаких других элементов.
Разность
,
и не содержащее никаких других элементов.
Разность ![]() и
и ![]() обозначается
обозначается
![]() или
или
![]() .
.
Обозначение
![]() употребляется в тех случаях, когда
употребляется в тех случаях, когда ![]() является собственным подмножеством
является собственным подмножеством ![]() рис.3.
рис.3.

A-B
Рис. 3.
В
остальных случаях употребляется ![]() рис.4.
рис.4.

Рис. 4.
Если
![]() является собственным подмножеством
является собственным подмножеством ![]() ,
то выполняется равенство
,
то выполняется равенство ![]() ,
а в остальных случаях нет. Разность двух
множеств
,
а в остальных случаях нет. Разность двух
множеств ![]() также можно записать в виде
также можно записать в виде
![]()
Через характеристические функции операция разности запишется как
![]() ,
для
,
для
![]() (2.18)
(2.18)
Приведем таблицу истинности для разности, исходя из формулы (2.18)
Таблица 3.
Таблица истинности для разности
|
|
|
|
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
1 |
0 |
Введем понятие импликации как дополнение к разности, то есть
![]() (2.19)
(2.19)
или через характеристические функции
![]() .
(2.20)
.
(2.20)
Таблица истинности для импликации, согласно (2.20) имеет вид
Таблица 4.
Таблица истинности для импликации
0
0
1
1
0
0
0
1
1
1
1
1
![]()
![]()
![]()
Используя операцию разности стрелку Пирса можно представить как
![]() ,
(2.21)
,
(2.21)
а через характеристические функции
![]() .
.
Тогда таблица истинности для стрелки Пирса будет иметь вид
Таблица 5.
Таблица истинности для стрелки Пирса
0
0
1
1
0
0
0
1
0
1
1
0
![]()
![]()
![]()
Операция разности позволяет представить штрих Шиффера как
![]() ,
(2.22)
,
(2.22)
а через характеристические функции
![]() .
.
Приведем табдицу истинности для штриха Шиффера
Таблица 6.
Таблица истинности для штриха Шиффера
|
|
|
|
|
0 |
0 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
1 |
0 |
На языке логических формул для стрелки Пирса имеет место
![]() ,
,
![]() , (2.23)
, (2.23)
а для штриха Шиффера –
![]() ,
,
![]() .
(2.24)
.
(2.24)
Иногда вводится понятие симметрической разности
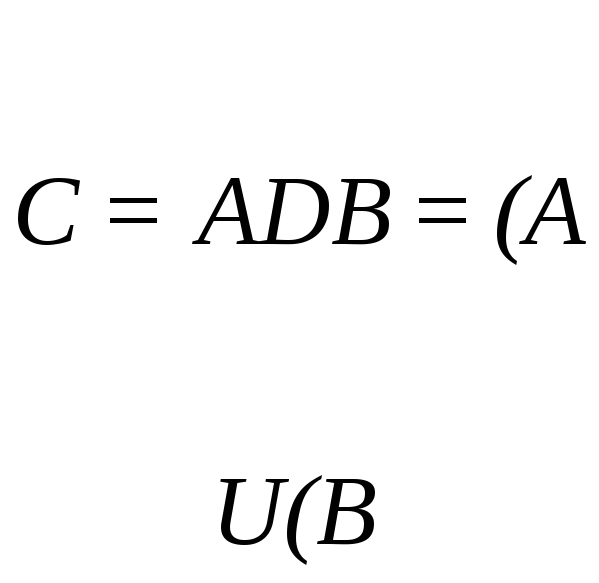 ,
,
представленной на рис.5 заштрихованной частью.

Рис. 5
Симметрическую разность можно представить и другим образом
![]() .
.
Исходя из этого выражения, симметричную разность легко записать через характеристические функции в алгебраическом виде
![]() ,
для
,
для
![]() . (2.25)
. (2.25)
Операции объединения и пересечения могут быть записаны с точки зрения логики:
![]() ,
для
,
для
![]() , (2.26)
, (2.26)
![]() ,
для
,
для
![]() . (2.27)
. (2.27)
Здесь
![]() и
и ![]() называются операциями взятия максимума
(дизъюнкция) и минимума (конъюнкция), то
есть взятие наименьшего и наибольшего
значений.
называются операциями взятия максимума
(дизъюнкция) и минимума (конъюнкция), то
есть взятие наименьшего и наибольшего
значений.
Рассмотрим
операцию эквивалентности,
дополняющую операцию симметрической
разности. Эквивалентность
определяется
общими элементами подмножеств ![]() .
Элементы, не входящие ни в
.
Элементы, не входящие ни в ![]() ,
также считаются эквивалентными:
,
также считаются эквивалентными:
![]() .
(2.28)
.
(2.28)
Через характеристические операция эквивалентности примет вид
![]() ,
для
,
для
![]() (2.29)
(2.29)
Таблица 7.
Таблица истинности для симметрической разности
-

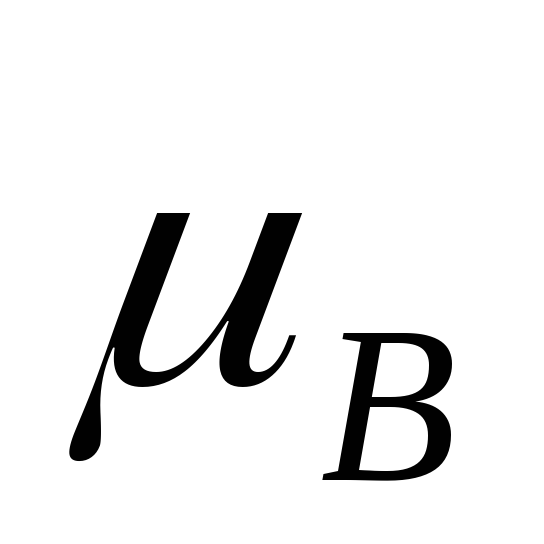
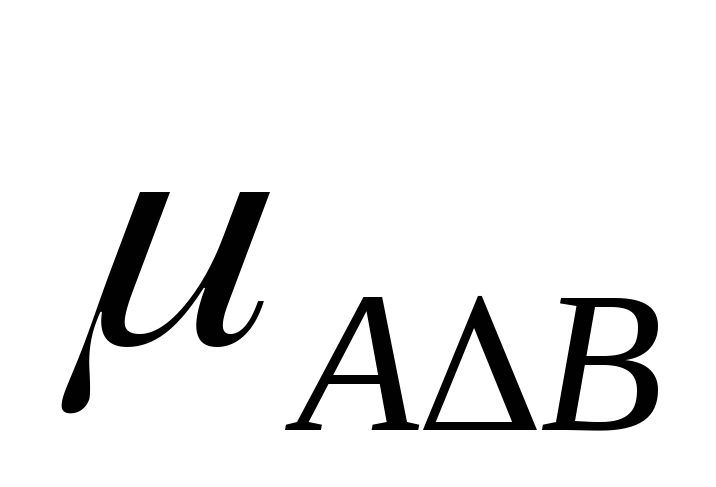
0
0
0
1
0
1
0
1
1
1
1
0
Таблица 8.
Таблица истинности для эквивалентности
-

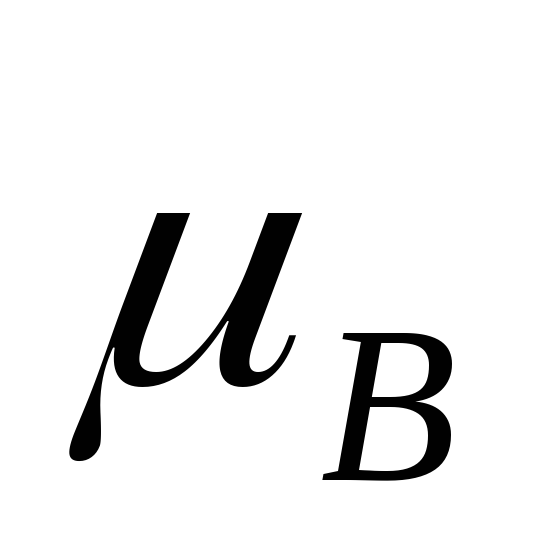
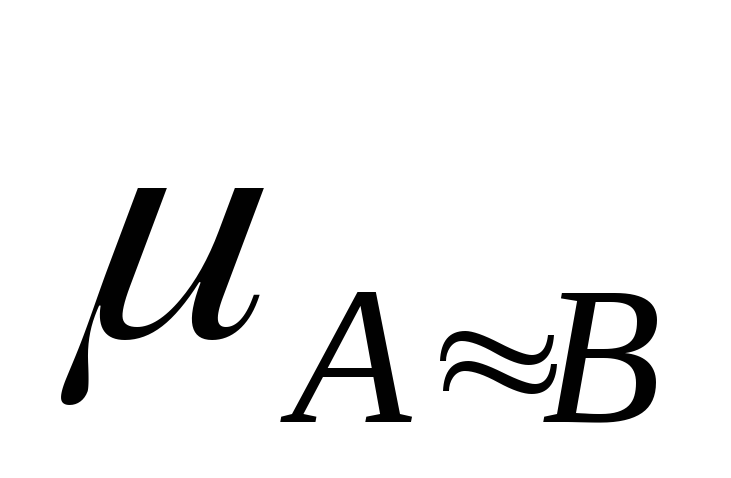
0
0
1
1
0
0
0
1
0
1
1
1
Введем
еще одну операцию дополнения
некоторого множества ![]() до полного
(универсального множества
до полного
(универсального множества ![]() ).
Это будет множество
).
Это будет множество ![]() ,
которое можно определить как
,
которое можно определить как
![]() или
или
![]() ,
для
,
для
![]() .
(2.30)
.
(2.30)
Для введенных выше операций над множествами можно сравнительно легко доказать следующие свойства:
1) закон идемпотенции
![]()
![]() ;
(2.31)
;
(2.31)
2) закон коммутативности относительно пересечения и суммы
![]()
![]() ,
,
![]() (2.32)
(2.32)
3) закон ассоциативности
![]()
![]() ,
(2.33)
,
(2.33)
![]() .
(2.34)
.
(2.34)
4) закон абсорбции
![]() ,
(2.35)
,
(2.35)
5) закон дистрибутивности
![]() ,
(2.36)
,
(2.36)
![]() .
.
6) закон комплементарности
![]() ,
,
![]() .
(2.37)
.
(2.37)
Аналогичные равенства выполняются и для логических функций, которые имеют соответствующие названия:
![]() -
противоречие,
-
противоречие,
![]() -
тавтология.
-
тавтология.
Отметим еще два важных свойства, справедливых в булевой алгебре:
двойное отрицание
![]() ;
(2.38)
;
(2.38)
закон де Моргана
![]() ,
,
![]() .
(2.39)
.
(2.39)
