ТМиВС 8вариант

ТМиВС

Я не смогла сделать только 5 задание, в 8 задании – график, и 9-интервальные оценки и в 10-последний поппункт.

Вариант № 8

1. Найти вероятность того, что дни рождения 12 человек придутся на разные месяцы года.

Решение:

Т.к.каждый из 12 человек может родится в любом из 12 месяцев года, то число всех возможных вариантов можно посчитать по формуле размещений с повторениями:

Число благоприятных случаев получим, представляя месяцы рождения у этих 12 человек, т.е.

M=P₁₂=12!.

Тогда искомая вероятность будет равна:

Ответ: Р=0,000054

2. Вероятность, что студент сдаст первый экзамен, равна 0.8, второй – 0.7, третий – 0.6. Вычислить вероятность того, что студент сдаст более двух экзаменов.

Решение:

Т.к. 3 экзамена, а нам следует вычислить вероятность того, что студент сдаст >2 экзаменов, то нужно найти вероятность того, что студент сдаст все 3 экзамена.

Пусть событие D – студент сдаст все 3 экзамена, тогда:

Ответ: Р=0,336

3. В 3 урнах находятся белые и черные шары. В первой 2 белых и 3черных, во второй 2 белых и 2 черных, в третьей 3 белых и 1 черный. Из первой урны переложили шар во вторую. После этого шар из второй урны переложили в третью. Наконец из третьей урны шар переложили в первую. Чему равна вероятность того, что состав шаров во всех урнах не изменится?

Решение:

Что бы прежний состав урны, надо вытащить шар того же цвета, что и положенный.

Введем гипотезы: Н₁-из первой урны вытащили белый шар, Р(Н₁)=; Н₂-из первой урны вытащили черный шар, Р(Н₂)=.

Событие А-состав урн остался прежним. По формуле полной вероятности, вычисляем:

Ответ: Р(А)=0,34

4. Игральная кость брошена 12 раз. Найти вероятность выпадения шестерки 5 раз.

Решение:

Решаем, по формуле Бернулли:

n-количество испытаний, k=количество появления события; p-вероятность появления события в одном испытании: q=1-p.

Получаем:

n=12; p=;q=

Подставляем значения в формулу:

Ответ: Р=0,030

4. В страховом обществе застраховано 11000 автолюбителей. Размер страхового взноса равен 10 у.е., а в случае аварии страховое общество выплачивает 1000 у.е. Какова вероятность что страховое общество к концу года разорится, если вероятность автолюбителю попасть в аварию равна 0,006?

НЕ РЕШЕНА!!!!!! Не знаю, как решить=(

4. Вероятность поражения цели при одном выстреле равна 0.5. Случайная величина (СВ) Х – число поражений цели при трех выстрелах. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график.

Решение:

Случайная величина Х- число поражений цели при 3 выстрелах. В n=3 независимых испытаниях вероятность того, что скоростной режим не нарушен, по условию постоянна и равна p=0.5. Следовательно, вероятность поражения: q=1-p=0.5

Следовательно ряд распределения, будет следующим:

P(0)=0.5³=0,125

P(1)=

P(2)=

P(3)=1*

xi	0	1	2	3
pi	0,125	0,375	0,375	0.125

Функция распределения:

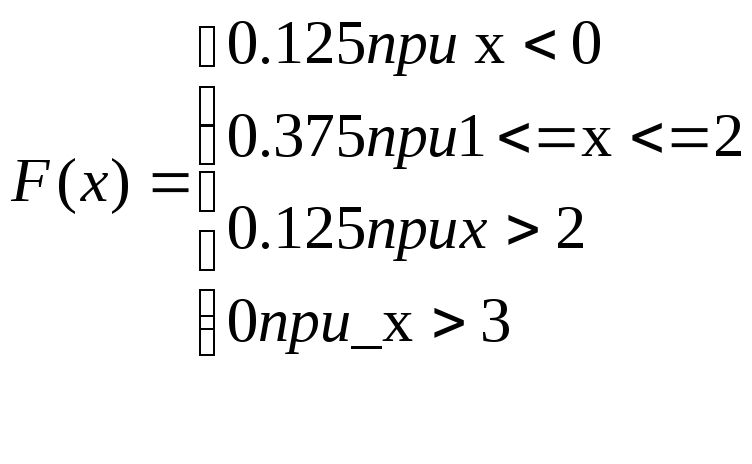
0,4

A₂ А₃

0,375

0,2

А₁ A₄

0,125

-1 1 2 3 А₅

А₀

4. Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения

xi	-1	1	3	5
pi	0,1	0,2	0,3	0,4

Решение:

Функция распределения:

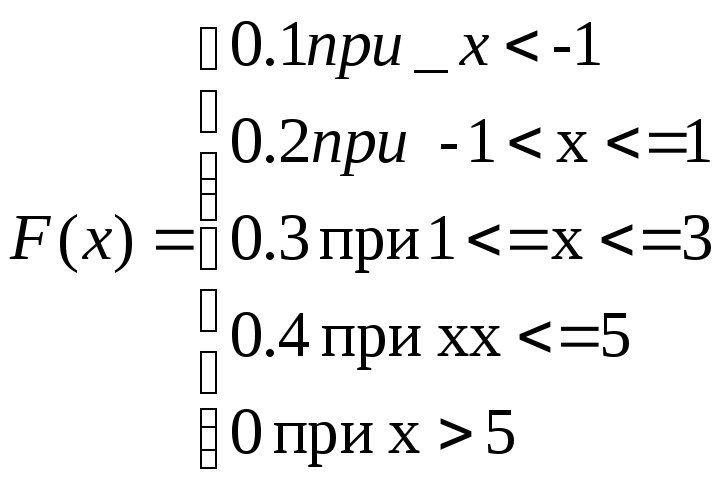
На оси Х откладываем значения х_i, равные -1,1,3,5, а по вертикальной оси вероятности этих значений:

А₄

0,4

А₃

0,3

А₂

0,2

А₁

0,1

-1 1 2 3 4 5 А₅

А₀

Вычислим математическое ожидание:

M(x)=

Вычислим дисперсию:

D(x)=M(x²)-(M(x))²

M(x²)=

(M(x))²=3²=9

D(x)=13-9=4

4. Плотность вероятности случайной величины Х равна

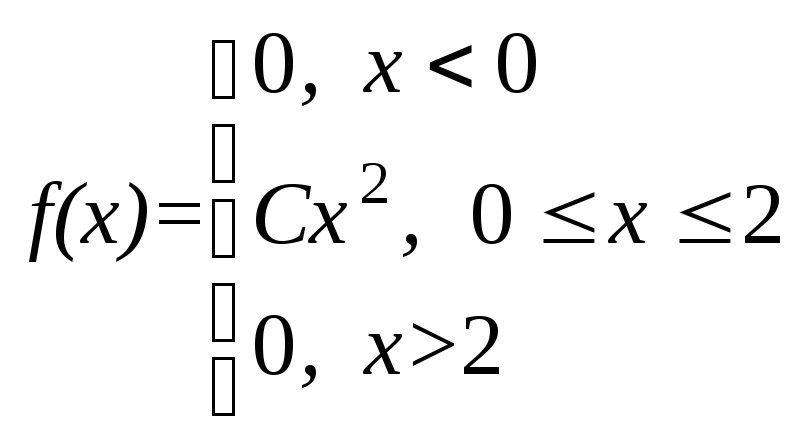
Найти постоянную С, функцию распределения F(x), математическое ожидание, дисперсию и вероятность попадания СВ на отрезок [0, 1]. Построить графики функций F(x) и

Решение

Вычислим значение константы С из условия нормировки:

с=

Определим функцию распределения F(x):

для x<0:

для

для

Окончательно:

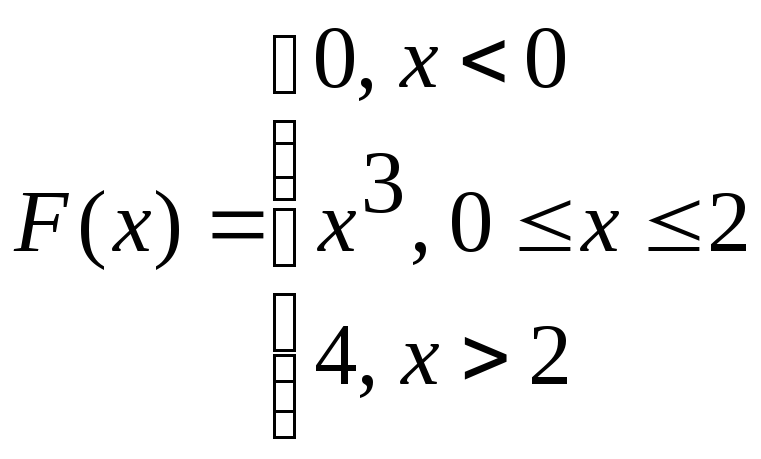
Вычислим вероятность :

Вычислим математическое ожидание:

Вычислим дисперсию:

Прости дальше решить не получается( С такими графиками, у меня проблема(

9. По выборке одномерной случайной величины

• построить график эмпирической функции распределения ,

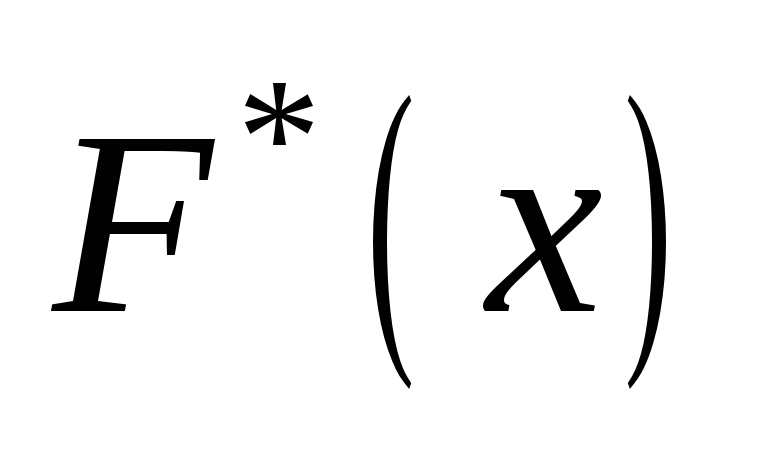• построить гистограмму относительных частот равноинтервальным способом,

• вычислить точечные оценки математического ожидания и дисперсии,

• вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности , не знаю.(

• выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости .

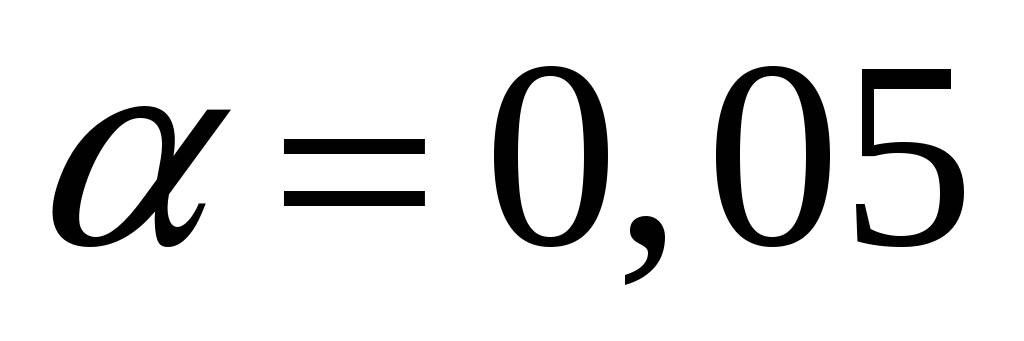Одномерная выборка:

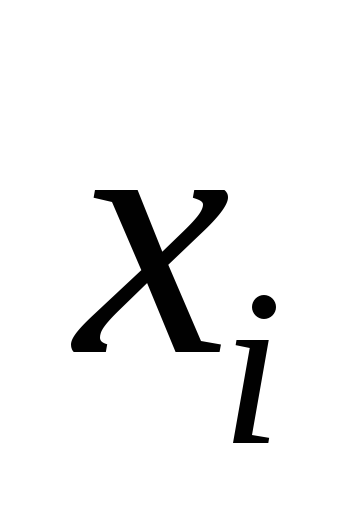
	18-20	20-22	22-24	24-26	26-28
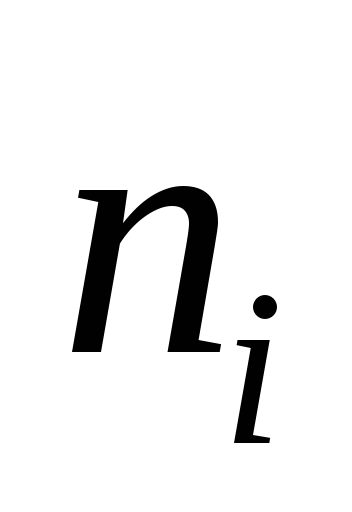
	15	27	61	29	18

График эмпирической функции:

Эмпирическая функция распределения Fn(x), определяется следующим образом:

,

где n_x – число вариант меньших х (х принадлежит R), n – объем выборки.

График эмпирической функции:

F*(x)

0,19

0,18

0,17

0,16

0,15

0,14

0,13

0,12

18 20 22 24 26 28 x

Построим гистограмму относительных частот равноинтервальным способом:

61

29

27

18

15

18 20 22 24 26 28

Вычислим точечные оценки математического ожидания и дисперсии

Номер наблюдения i	1	2	3	4	5	Сумма значений в строке
Левая граница ai	18	20	22	24	26
Правая граница bi	20	22	24	26	28
Частота тi	15	27	61	29	18
Середина интервала хi	19	21	23	25	27
хiтi	285	567	1403	725	486
Отклонение от среднего	-18,2	-20,2	-22,2	-24,2	-26,2
	-273,5	-546,3	-1356,2	-702,8	-472,2
	4986,8	11053,5	30153,6	17030,4	12387,4

Несмещенной оценкой математического ожидания является среднее арифметическое:

Выборочная дисперсия определяется по формуле:

S=22.45

При уровне значимости а=0,05 проверить гипотезу о нормальном законе распределения:

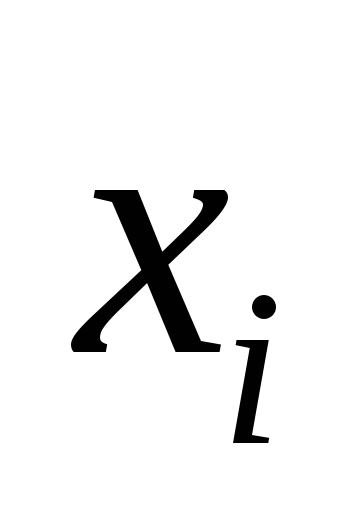
	18-20	20-22	22-24	24-26	26-28
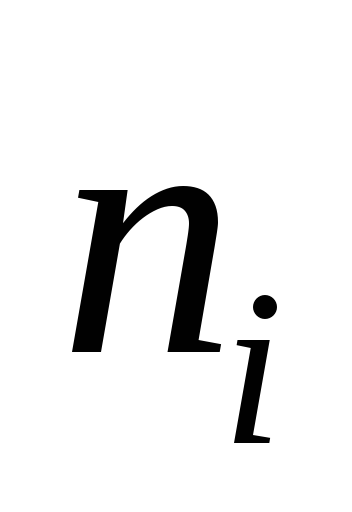
	15	27	61	29	18

10. По корреляционной таблице двумерной случайной величины

• вычислить выборочный коэффициент корреляции ,

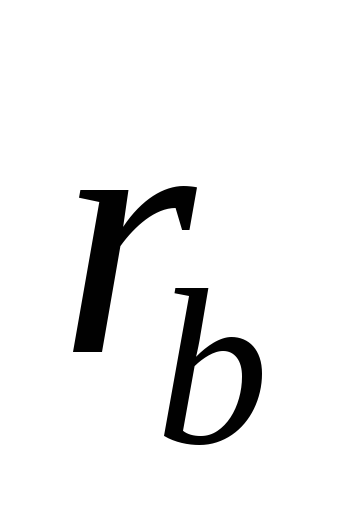• проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе 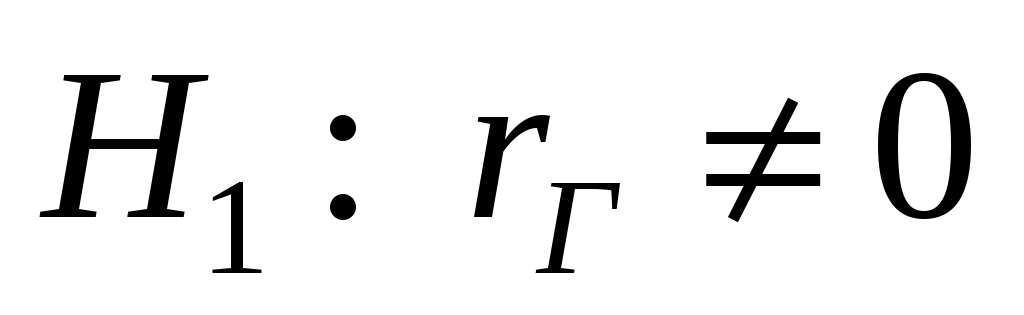при уровне значимости ,

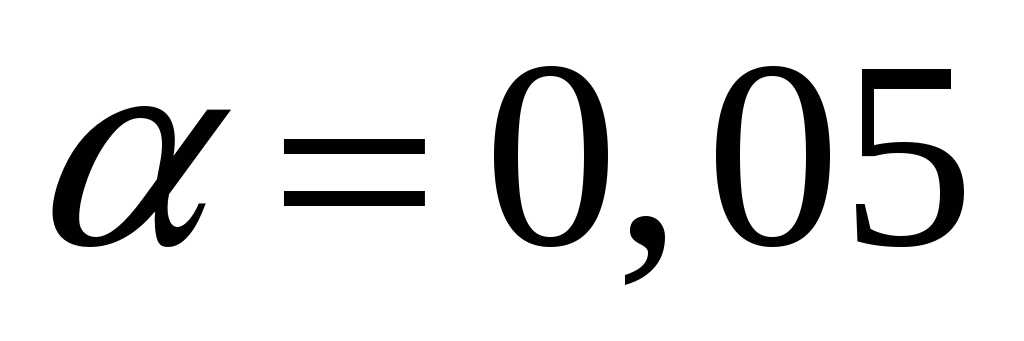• найти эмпирическое уравнение 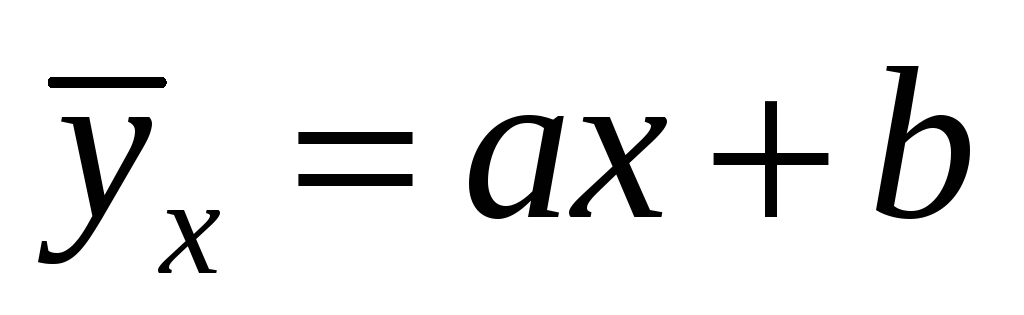прямой лини регрессии на .

Корреляционная таблица:

	20	22	24	26	28	30	32
30	-	6	-	4	-	2	5
40	4	-	5	-	7	1	-
50	-	4	3	5	-	-	6
60	5	3	-	-	10	2	-
70	-	4	10	4	2	8	-

Выборочный коэффициент корреляции:

Найдем необходимые числовые характеристики.

Выборочные средние:

=(20*9+22*17+24*18+26*13+28*19+30*13+32*11)/100=25.98

=(30*17+40*17+50*18+60*20+70*28)/100=52.5

Дисперсии:

σ2x = (20²*9+22²*17+24²*18+26²*13+28²*19+30²*13+32²*11)/150-25.98²=13.48

σ2y = (30²*17+40²*17+50²*18+60²*20+70²*28)/100-52.5²=210.75

Откуда получаем среднеквадратические отклонения:

σ_x = 3.672 и σ_y = 14.51

Cov(x,y) =(30*22*6+30*26*4+30*30*2+30*32*5+40*20*4+40*24*5+40*28*7+40*30*1+50* 22*4 + 40*24*3+50*26*5+50*32*6+60*20*5+60*22*3+60*28*10+60*30*2+70*22*4+70* 24*10 +70*26*4+70*28*2+70*30*8)/100-(25.98*52.5)=1361.4-1363.95=-2.55

Определим коэффициент корреляции

Значимость коэффициента корреляции:

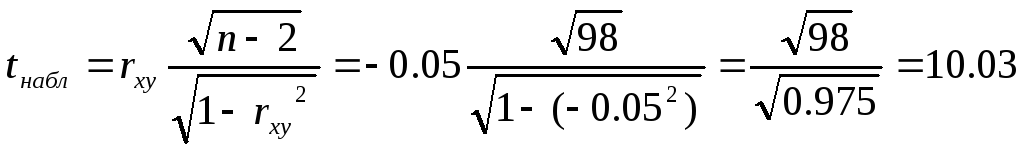
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=100-m-1 = 98 находим t_крит:

t_крит (n-m-1;α/2) = (98;0.025) = 1.984

где m = 1 - количество объясняющих переменных.

Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).

Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим.

А эмпирическое уравнение прямой лини регрессии на . – прости честно не помню как решала, меня не получается тебе решить. Прости.