24.05.03
Московский Государственный Университет им. М.В.Ломоносова
Физический факультет
Исследование маятника с колеблющейся точкой подвеса.
Курсовая работа по курсу «Компьютерные методы в физике» Студента 214 группы Хижняка Евгения Евгеньевича
Преподаватель: доцент С. А. Шленов
г. Москва, 2003
Введение
В
данной работе изучаются негармонические
колебания: исследуется поведение
маятника с колеблющейся (в вертикальной
плоскости) точкой подвеса. Уравнение
движения, описывающее колебания данного
маятника, отличается от уравнения
движения обычного гармонического
осциллятора добавлением нелинейного
члена Sin(
),
и записывается в виде:
(1)
Где:
-
Параметр, характеризующий затухание
(потерю энергии) системой,
-
Собственная частота маятника,
-
Частота вынуждающей силы,
-
Амплитуда вынуждающей силы.
Поведение такого маятника сильно зависит от начальных условий. В общем случае маятник может вести себя как:
а) Обычный гармонический осциллятор
б) Субгармонический осциллятор
в) Квазипериодический осциллятор
г) Хаотический осциллятор (непредсказуемая система)
Первые три вида колебаний относятся к классическим аттракторам. Последний вид подразделяются на обычные (совершенно непредсказуемые) колебания, и на так называемый "странный" аттрактор. Поведение "странного " аттрактора является хаотическим, т.к. мы не можем точно определить положения маятника в наперед заданное время. Однако при определенных методах исследования его поведение можно аппроксимировать при помощи геометрического объекта - фрактального множества. Изучение условий возникновения хаотических колебания, а так же проявления "странного" аттрактора и его поведения является одной из интереснейших и наиболее информативной целью нашей работы. [1]
Теория
Уравнение колебаний нашего маятника (1) является частным случаем уравнения Матьё для колебаний при параметрическом воздействии, которое записывается как:
(2)
Где
и
соответственно
параметр и глубина модуляции.
Полный анализ решений уравнения Матьё довольно сложен, особенно для нашего (нелинейного) случая. Решение уравнения (2) обычно записывается в виде:
(3)
Где
- ограниченные функции, с периодом
равным периоду или половине периода
изменения параметра
,
и
- комплексная величина, называемая
характеристическим показателем,
вещественная часть которой определяет,
имеет ли решение возрастающий характер
или нет.
Области значений нарастающих колебаний (т.е. возникновения параметрического резонанса) были в 1927 г. рассчитаны советскими учеными А. А. Андроновым и М. А. Леонтовичем, и изображены на рис 1. Заштрихованные области соответствуют нарастающему процессу, а вне этих областей в нашем случае (диссипативной системы) наблюдается затухающий процесс колебаний.
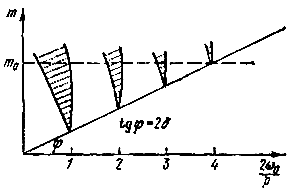
Рис. 1. Области параметрического возбуждения для системы с затуханием.
Из
рисунка видно, что для одного значения
,
при возрастании глубины модуляции 
(аналогичный
параметр нашей системы - амплитуда
вынуждающей силы 
)
процесс будет периодически затухающем
(начиная с затухания при малом 
)
до определенного значения, после которого
затухающий процесс больше встречаться
не будет, т.к. “клины” областей
параметрического возбуждения при
определенном 
для
выбранного значения 
сомкнутся.
Именно эту зависимость от глубины
модуляции 
(или
)
мы и изучаем. [2]
Однако в заштрихованной области рассматриваемый нами маятник ведет себя как недетерминированной система, в которой движение маятника подразделяется на несколько возможных классов. Перечислим их:
Классы движений в нелинейных детерминированных системах
а) Предсказуемое регулярное движение: периодические колебания, квазипериодическое движение. Система не является чувствительной к изменению параметров и начальных условий.
б) Непредсказуемое регулярное движение: регулярные множественные аттракторы. При достаточно большом времени исследования характер движения чувствителен к начальным условиям.
в) Переходный хаос: движения, которые кажутся хаотическими и не имеют характерных свойств "странного" аттрактора. При длительном времени исследования вырождаются в регулярное движение.
г) Перемежаемый хаос: регулярное периодическое движение, прерываемое переходными вспышками хаотического движения. Длительность периодов регулярного движения непредсказуема.
д) Ограниченный (узкополосный) хаос: хаотические движения, орбиты которых проходят в фазовом пространстве вблизи от орбит некоторых периодических или регулярных движений. Спектры часто имеют расширение определенных частотных компонент.
е) Слабый крупномасштабный или широкополосный хаос: хаотические орбиты охватывают обширные области фазового пространства. Спектры состоят из широкого набора частот, особенно меньших частот возбуждения (если последние присутствуют).
ж) Сильный крупномасштабный хаос: динамические свойства можно описать только в фазовом пространстве очень большого числа измерений. Система имеет очень большое число степеней свободы, поэтому трудно оценить её фрактальную размерность. [3]