Курсовая работа.

Задача №19.

Елецкий Александр 216гр.

1) Физическая модель.

В задаче необходимо построить фазовый портрет и график x(t) для уравнения, описывающего смещение x электронного облака в атоме под действием монохроматической световой волны. Получим это уравнение.

Используя второй закон Ньютона, уравнение движения осциллятора запишем в виде

(1)

Здесь m – масса электрона, e – заряд электрона, x – смещение центра электронного облака относительно атомного ядра (рис. 1), Е – амплитудное значение напряженности электрического поля световой волны, p – круговая частота волны, Fвозвр – возвращающая сила, обусловленная притяжением электрона к ядру и связанная с потенциальной энергией U(x) электрона в поле ядра соотношением

(2)

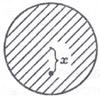
Рис. 1. Классическая модель атома

В окрестности положения равновесия электрона (x=0) потенциальную энергию U(x) можно представить в виде разложения по степеням x:

(3)

График зависимости потенциальной энергии от электронной координаты схематически показан на рис. 2. Первое слагаемое в (3) соответствует параболическому приближению (пунктир на рис. 2). Остальные слагаемые описывают отличие формы реальной потенциальной ямы от параболической. Учет этих слагаемых важен, если амплитуда колебаний электрона достаточна велика. Последнее может иметь место в поле световой волны большой интенсивности. Подставив (3) в (2), получим

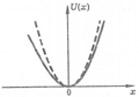
Рис. 2. График потенциальной энергии нелинейного осциллятора (сплошная кривая) и линейное приближение (пунктир)

(4)

Таким образом, возвращающая сила оказывается нелинейной функцией смещения. Подставляя (4) в (1) и ограничиваясь учетом первой нелинейной поправки, получим уравнение

(5)

где - собственная частота колебаний осциллятора,- параметр нелинейности возвращающей силы. Добавим в левую часть уравнения (5) слагаемое, описывающее затухание электронных колебаний. В итоге получим уравнение

(6)

где - время затухания колебаний электрона. Итак, уравнение (6) описывает колебания атомного осциллятора под действием поля световой волны.

2) Математическая модель.

Чтобы перейти к математической модели, надо обезразмерить наше уравнение. Для этого поделим x на значение в особой точке, а t умножим на ω – размерность сократится. Чтобы найти особые точки, проведем линейный анализ устойчивости стационарных решений. Сначала разложим наше уравнение на систему двух дифференциальных уравнений первого порядка и исключим косинус, т.к. линейный анализ выполняется только для автономных функций (где t в явном виде отсутствует)

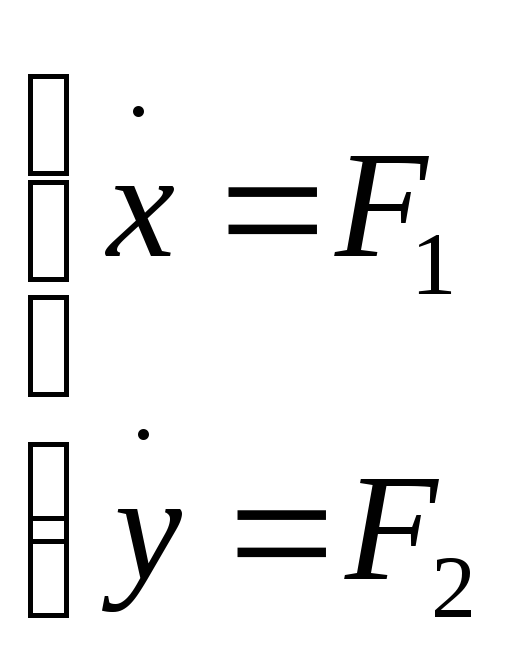
Находим особые точки из условия

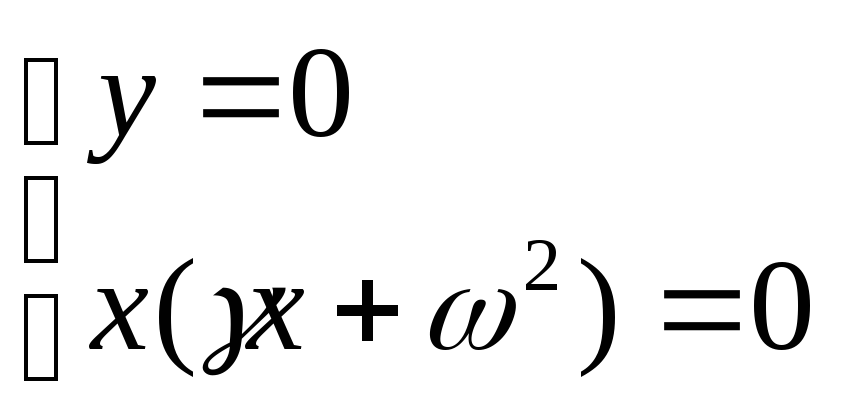
Особые точки:

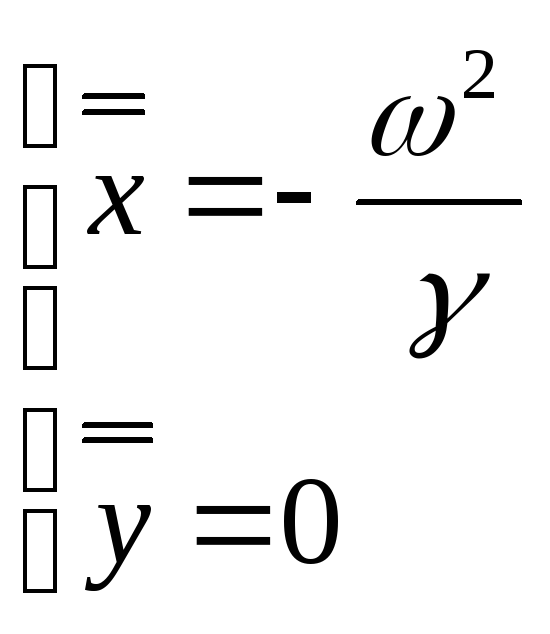
Поделив намы получим безразмерную координату. Подставив в исходное уравнениеии преобразовав его, получим

где x и t теперь безразмерны, - коэффициент затухания собственных колебаний,- амплитуда вынуждающей силы, а- соотношение частот вынуждающей и собственной. Теперь особые точки и функцииибудут иметь вид:

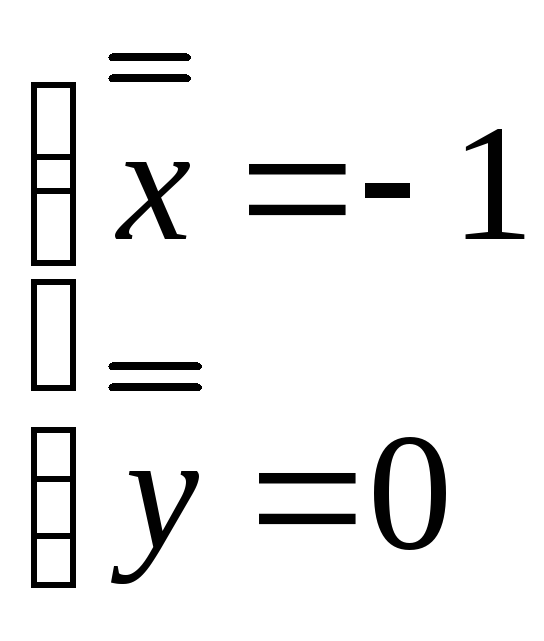
Найдем коэффициенты для характеристического уравнения

а) особая точка (0;0)

характеристическое уравнение имеет вид:

Если подкоренное выражение меньше нуля (), тоp примет вид :

< 0, значит эта особая точка является устойчивым фокусом.

Если же подкоренное выражение больше либо равно нулю (, что практически невозможно, т.к.=> изследует, т.е. время затухания на порядок меньше, чем 1 период колебаний), то

и < 0

значит при эта точка является устойчивым фокусом, а при- устойчивым узлом

б) особая точка (-1;0)

характеристическое уравнение имеет вид:

значит эта особая точка - неустойчивое седло.