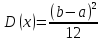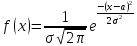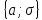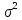shpory2 семестр Рапа
.docx
Событие – всякий факт, который в результате испытания может произойти или не произойти. Случайный опыт – любое действие, которое можно повторить большое число раз в одинаковых условиях и результаты которого нельзя предугадать заранее. Пространство элементарных событий (ПЭС): Ω – множество, состоящее из предполагаемых исходов данного опыта, исключающих друг друга. Элементы множества Ω – элементарные события. Случайное событие – произвольное подмножество ПЭС. Вероятность
события A
– P(A)
– сумма вероятностей элементарных
событий, образующих это событие.
Численная мера степени объективной
возможности этого события.
Условия
для вероятности элементарного события
ЭЛЕМЕНТАРНЫЕ события – содержат 1 исход (элементарный исход). СОСТАВНЫЕ события – содержат несколько исходов.
|
Равенство: События А и В равны, если каждое из них является частным случаем другого. А=В, т.е. А является частным случаем события В, при наступлении А наступает В. Сумма двух событий А и В: событие С, состоящее в появлении хотя бы одного из двух событий. А+В=С. В событие С входят все элементарные исходы, содержащиеся «или А, или В». Произведение событий А и В: событие С, состоящее в совместном появлении двух событий. АВ=С. «и А, и В». Разность (А-В): событие С, которое содержит те элементы А, которые не входят в В.
|
СОВМЕСТНЫЕ.
События совместны, если каждое из них
содержит хотя бы одно общее элементарное
событие, т.е. если АВ≠ НЕСОВМЕСТНЫЕ.
События несовместны, если появление
одного из них исключает появление
других событий в одном и том же испытании
(т.е. не имеют общих элементарных
исходов). АВ=
|
ДОСТОВЕРНОЕ. Событие, которое обязательно произойдет в результате выполнения фиксированной совокупности условий. Р(А)=1 ПРОТИВОПОЛОЖНОЕ.
Событие
|
Пространство
элементарных исходов называется
дискретным,
если оно конечно и счётно. Ω={ Вероятность
события в дискретном пространстве
определяется
как сумма вероятностей каждого из
элементарных исходов, входящих в это
событие.
Свойства вероятности в дискретном пространстве:
|
|
6. Теорема сложения вероятностей для несовместных и совместных событий. Д/СОВМЕСТНЫХ:
Вероятность
суммы двух совместных событий выражается
разностью между суммой вероятностей
этих событий и вероятностью из
произведения.
Д/НЕСОВМЕСТНЫХ:
Вероятность суммы для несовместных
событий равна сумме вероятностей этих
событий.
|
7. Понятие условной вероятности. Теорема умножения вероятностей. Независимые и зависимые события. Условная
вероятность события А при наличии
события В –
вероятность события А, вычисленная
при условии, что событие В произошло.
Единственная
формула нахождения условной вероятности:
«Как общее относится к базе(к тому, что произошло)». Условие: P(B)>0 Теорема
умножения вероятностей: вероятность
произведения двух событий равна
вероятности одного из них, умноженной
на условную вероятность другого
события при наличии первого.
ЗАВИСИМЫЕ события: события А и В зависимы, если появление события А изменяет вероятность появления события В (и наоборот). НЕЗАВИСИМЫЕ
события:
если появление события А не зависит
от того, произошло ли событие В или
нет. Теорема умножения вероятностей
для независимых событий:
|
8. Формула полной вероятности. Применяется, если об опыте можно сделать n исключающих друг друга гипотез H1, H2,..., Hn, а также, если событие А может появиться только при одной из этих гипотез.
Свойство
системы гипотез Hi:
|
9. Формула Байеса Р(H1), P(H2),…, P(Hk) – вероятности гипотез, априорные (доопытные); событие А – апостериорное (полученное в результате опыта). По формуле Байеса, условная вероятность того, что имело место событие Hk, если в результате опыта наблюдалось событие А, вычисляется по формуле (условная вероятность гипотезы при событии):
|
10. Схема испытаний Бернулли. Предполагает серию однотипных опытов (испытаний). Исход каждого опыта независим от исходов других. Например: а) многократное извлечение из урны одного шара, при условии, что вытянутый шар после регистрации его цвета кладется обратно в урну. б) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой. Испытание
имеет 2 исхода: 1) появится событие А;
2) появится событие
n независимых испытаний Бернулли (вероятность появления события А в каждом отдельном испытании постоянна. Испытания проводятся в одинаковых условиях). p – вероятность появления события А: p=P(A). q
– вероятность
появления противоположного события
Тогда
вероятность того, что событие А появится
в серии n
испытаний ровно k
раз
Pn(k)=
|
Случайные события
|
11. Локальная теорема Лапласа. Позволяет приближенно найти вероятность появления события в серии однотипных n испытаний ровно k раз, если число испытаний достаточно велико. Формулировка теоремы: Если вероятность появления события А в каждом испытании постоянна и отлична от нуля и единицы (0<p<1), то вероятность Pn (k) того, что событие А появится в серии однотипных n испытаний ровно k раз, приближенно равна значению функции:
Конечная
формула:
|
12. Интегральная теорема Муавра-Лапласа. Применяется для вычисления вероятности P(l<k<m) того, что событие А появится в серии n испытаний не менее l и не более m раз (от l до m раз). Формулировка теоремы: Если вероятность p наступления события А в каждом испытании постоянна и отлична от 0 и 1 (0<p<1), то вероятность P(l<k<m) того, что событие А появится в серии n испытаний от l до m раз, приближенно равна след. интегралу:
при
|
|
|
|
Комбинаторика
|
1.Выборка с возвращением, выборка без возвращения. Размещения, перестановки, сочетания. Как перестановки, так и размещения, были определены как последовательности элементов некого множества Y. Перестановки, составленные из элементов этого множества, отличаются друг от друга только порядком расположения элементов в последовательностях, размещения – как порядком элементов, так и самими элементами. Сочетания – это такие наборы элементов множества Y, которые отличаются друг от друга только самими элементами, порядок расположения элементов в них не учитывается. Договоримся, в дальнейшем называть перестановки, размещения и сочетания общим словом "расстановки". Сочетания, также, как и расстановки других видов, могут содержать одинаковые элементы или не содержать. В зависимости от этого различают сочетания с повторениями или без повторений. Сочетаниями без повторений или выборками без возвращений из n по m называют подмножества множества Y, (n(Y)=n), причем каждое подмножество содержит m элементов. Примечание. В теории вероятностей сочетания без повторений называют выборками без возвращений. Термин "выборка" подразумевает, что при составлении подмножества один за другим извлекается m элементов множества Y , причем извлеченные элементы в множество не возвращаются и второй раз в подмножестве появиться не могут.
Сочетаниями с повторениями или выборками с возвращениями из n по m называют наборы элементов множества Y, (n(Y)=n), каждый из которых содержит m элементов, причем, наборы отличаются друг от друга составом элементов, но порядок расположения элементов не учитывается, элементы в наборах могут повторяться. Примечание. В теории вероятностей сочетания с повторениями называют выборками с возвращениями. При составлении подмножества один за другим извлекают m элементов множества Y, причем извлеченный элемент возвращается в множество Y и может быть извлечен повторно.
Число сочетаний
с повторениями из n
по m
обозначают
|
Случайная величина – это величина, которая в результате испытания примет только 1 возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее нельзя учесть. Дискретная случайная величина – случайная величина, принимающая отделенные друг от друга значения, которые можно перенумеровать (число возможных значений конечное и счётное). Если между случайными величинами, отмеченными на координатной прямой, существуют промежутки, не содержащие других возможных значений, то эти сл. величины относятся к классу дискретных. Способы задания дискретной сл. величины (ДСВ). Закон распределения ДСВ – всякое соответствие между возможными значениями сл. величины xi и вероятностями их появления pi.
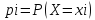 , ,

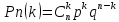
|
Математическое
ожидание –
важная числовая характеристика
случайной величины. Приближенно равно
среднему значению случайной величины.
Это сумма произведений всех возможных
значений ДСВ (xi)
на их вероятности (pi).
Свойства мат. ожидания:
Отклонение
сл. величины от ее мат. ожидания –
разность между случайной величиной
и ее математическим ожиданием: x-M(x).
|
Дисперсия
ДСВ –
характеристика рассеяния (насколько
разбросано значение сл. величины).
Мат. ожидание квадрата отклонения сл.
величины от ее мат. ожидания.
Свойства дисперсии:
|
Дискретная случайная величина Х называется распределенной по биномиальному закону, если ее возможные значения 0,1,…,n, а вероятности того, что Х=k, выражаются формулой:
Таблица распределения Х:
Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон
распределения называют «биномиальным»
потому, что правую часть равенства
Вычисление мат. ожидания и дисперсии: M(x)=np; D(x)=npq, где q=1-p.
|
Неравенство Чебышева. Помогает оценить вероятность того, что отклонение сл. величины от ее мат. ожидания не превышает по абсолютной величине положительно числа ε. Если ε достаточно мало, то мы таким образом оценим вероятность того, что Х примет значения, достаточно близкие к своему мат. ожиданию. Формулировка:
Вероятность того, что отклонение сл.
величины Х от ее мат. ожидания по
абсолютной величине положительного
числа ε, не меньше, чем
Данное неравенство справедливо как для дискретных, так и для непрерывных сл. величин. Теорема Чебышева. Если
х1,
х2,…,
хn
– попарно независимые сл. величины,
причем дисперсии их равномерно
ограничены (не превышают постоянного
числа С), то, как бы мало ни было
положительное число ε, вероятность
неравенства
Теорема Бернулли. Если в каждом из n независимых испытаний вероятность p появления события А постоянна, то близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
ε – сколь угодно малое положительное число.
|
Случайные величины
Дискретная сл. величина Х называется распределенной по закону Пуассона, если ее возможные значения 0,1,2,…,k, а вероятность того, что Х=k, выражается формулой:
Вычисление мат. ожидания и дисперсии: M(x)=λ; D(x)=λ
|
Случайная величина с геометрическим распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха р. Говорят,
что сл. величина Х имеет геометрическое
распределение
с параметром p
Вычисление
мат.ожидания и дисперсии:
|
Функция
распределения (интегральная функция)
– функция F(x),
определяющая вероятность того, что
сл. величина Х в результате испытания
примет значение, меньшее x,
т.е.
Основные свойства функции распределения:
|
НСВ – сл. величина, возможные значения которой непрерывно заполняют какой-то промежуток. Плотность распределения вероятности НСВ – функция f(x) – первая производная от функции распределения F(x). f(x)=F’(x) (связь с интегральной функцией распределения). F(x) – первообразная для f(x). Свойства плотности распределения:
Если функция
плотности f
определена на интервале [a;b],
то
График плотности
f(x)
называется кривой распределения.
Функция F(x)
выражается через плотность распределения
формулой
|
Интегральная функция распределения:
Дифференциальная функция распределения (плотности вероятности):
Вычисление
мат. ожидания и дисперсии:
|
||||||||||||||||||||||||
Интегральная функция распределения:
Дифференциальная функция распределения (плотности вероятности):
Параметры
M(x)=a;
D(x)=
|
|
|
|
|
Математическая статистика
|
1. Выборка и генеральная совокупность. Способы представления выборки. Выборка – совокупность случайно отобранных объектов исследования. Генеральная совокупность – множество всех возможных значений исследуемого признака. Выборкой объема n из генеральной совокупности с функцией распределения Fx(x) называется последовательность x1,x2,…,xn наблюдаемых значений случайной величины X. Каждую выборку рассматривают как выборку из теоретически бесконечной генеральной совокупности, распределения признака в которой совпадает с теоретическим распределением вероятностей величины x. Способы представления выборки: а) Вариационным ряд – элементы выборки упорядочиваются по величине. б) Статистический ряд – для этого все n наблюдаемых значений выборки разбивают на k непересекающихся интервалов [ci,ci+1), i=1,…,k, обычно одинаковой длинны h. Формула Стерджеса k=[log2n]+1. в) Дискретный статистический ряд – при наблюдении дискретных случайных признаков довольно часто среди элементов выборки встречаются одинаковые. В виде таблицы записываем значение признаков в возрастающем порядке и частоту признака встречающегося в выборке. г) и в порядке регистрации. |
2. Вариационные и статистические ряды. Частота, относительная частота, размах выборки мода медиана, выборочное среднее к выборочная дисперсия. Вариационным рядом x1,x2,…,xn называется способ записи выборки, при котором элементы выборки упорядочиваются по величине. Разность между крайними членами вариационного ряда называется размахом выборки. Статистический ряд – для этого все n наблюдаемых значений выборки разбивают на k непересекающихся интервалов [ci,ci+1), i=1,…,k, обычно одинаковой длинны h. Формула Стерджеса k=[log2n]+1. Пусть событие Е состоит в том что значение случайной величины x принадлежит некоторому множеству SE и пусть дана случайная выборка значений величины х. Частотой события – называется количество vi выборочны значений xi. Относительной частотой – отношение частоты к объему выборки. Размах выборки - разность между крайними членами вариационного ряда называется размахом выборки. Мода - наиболее часто повторяющиеся значения признака. Xmo=x0+h(fmo-fmo-1/2fmo-fmo-1-fmo+1) Медиана – величина признака которая делит упорядоченную последовательность на две равные части. Me= x0+h(0,5*N+Sme-1/fme) Выборочное среднее – называется среднее арифметическое элементов выборки: xcp=nixi/n Выборочная дисперсия S2=1/n*[n сумма i=1](xi-xср)2 |
3. Эмпирическая функция распределения (функция накопительных частот). Это способ представления статистических данных. Эмпирической функцией распределения называется – функция F*(x)=vn(x)/n где vn(x) – число элементов выборки x1,x2,…,xn значения которых меньше x. Функция F*(x) постоянна на промежутках [xi, xi+1}=[ci, ci+1} для интервально группированных данных, а в концевых точках xi+1 увеличивается на p*i=vi/n, i=1, …, k-1: {0 при x<=x1 F*(x)= { p*i=vi/n при xi<x<=xi+1, i=1,…,k-1, {1 при x>xk. F*(x) однозначна для всех x и обладает всеми свойствами функции распределения: изменяется от 0 до 1 не убывает и непрерывна слева. Важнейшее свойство что при увеличении n происходит сближение F*(x) с теоретической функцией распределения F(x)=P(X<x). |
4. Графическое представление выборки (полигон и гистограмма). Полигон обычно используют для изображения дискретного статистического ряда. Для его построения на оси абсцисс откладывают все различные выборочные данные выборочные данные x1<x2<…<xk. На оси ординат, пользуясь статистическим рядом, либо частоты либо относительные частоты. Затем отмечают точки с координатами и соединяют. В силу закона больших чисел в схеме Бернули относительные частоты p*I сходятся по вероятностям pi=P(X=xi). Гистограмма – это графическое изображение интервального статистического ряда в виде прямоугольников разной высоты. Основаниями прямоугольников являются отрезки оси абсцисс, соответствующие интервалам группировки, а высоты соответствут относительным частотам интервалом. Функция: {0 при x<=c1 p*(x)= { v*i=(nh) при ci<x<=ci+1, i=1,…,k-1, {1 при x>ck+1. При достаточно большом объеме выборки и малых значения длин интервалов группировки гистограмма близка к плотности распределения исследуемого признака X. |
5. Точечные и интервальные оценки параметров. Основные свойства оценок на примере оценки математического ожидания. Выборочное среднее xcp=nixi/n Исправленная выборочная дисперсия |
|
6. Понятие доверительного интервала. Основные типы задач на интервальные оценки. Доверительным интервалом для параметра 0 называется интервал (0*1; 0*2) со случайными границами 0*1 и 0*2, который с заданной доверительной вероятностью Y=1-a накрывает неизвестное истинное значение параметра 0: P(0*1<0<0*2)=1-a. Нижняя и верхняя границы ДИ 0*1 и 0*2 определяются по результатам наблюдений и следовательно, являются случайными величинами. Часто применяются односторонние ДИ. Симметричный доверительный интервал P(0*-Е<0<0*+Е)=Р(|0-0*|<Е)=1-а.,Величина Е называется точностью – это половина длинны доверительно интервала, а – уровень значимости и Y надежность. Для мат.ожидания: xcp-+t1-a/2*(n-1)s/kor n Для дисперсии: (n-1)s2/X21-a/2(a/2)(n-1) Основные типы задач 1)определение доверительно интервала (точности E) по заданной доверительной вероятности Y=1-a и объему выборки n. 2)Определение доверительной вероятности Y=1-a по заданному интервалу (точности) и объему выборки n. 3)Определение объема выборки n по заданному доверительному интервалу и доверительной вероятности Y=1-a.
|
7.Интервальная оценка математического ожидания нормального распределения генеральной совокупности при неизвестной дисперсии. x ср-(t1-a/2(n-1)s/kor n)<M< x ср+(t1-a/2(n-1)s/kor n) xcp=nixi/n s2=(nixi2/(n-1))-(nxcp/(n-1)) |
8.Интервальная оценка дисперсии нормального распределения генеральной совокупности при неизвестной математического ожидания. ((n-1)s2)/(X21-a/2(n-1))<б2<((n-1)s2)/(X2a/2(n-1)) xcp=nixi/n s2=(nixi2/(n-1))-(nxcp/(n-1)) |
9. Общая постановка и схема проверки параметрической статистической гипотезы. Ошибки первого и второго рода при проверки гипотез. Подлежащая проверке гипотеза называется основной. Каждой основной гипотезе противопостовляют основную которую обозначают H1. в качестве альтернативной можно рассматривать одну из следующих гипотез H1(1):0>00; H1(2):0<00; H1(3):0=00; H1(4):0/=00; Вид такой гипотезы определятся конкретной формулировкой задачи. Схема проверки гипотезы: Этап 1. Сформулировать Н0 и Н1. Этап 2. Назначить уровень значимости а. Этап 3. Задать объем выборки n. Этап 4. Выбрать статистику vIv критерия и определить распределение статистики vIv при условии что верна H0. Этап 5. В зависимости от проверяемой и альтернативной гипотез выбрать область принятия гипотезы и критическую область. Определить критические точки. (пример хи квадрат) Этап 6. а) Н0 должна быть отвергнута на уровне значимости а, если вычисленное значение vIv* попадает в критическую область. б) Н0 принимается или её принятие откладывается, если вычисленное vIv* принадлежит допустимой области. Этап 7. Выполнить эксперимент и проверить гипотезу, т.е. получить выборку намеченного объема вычислить выборочное значение vIv* статистики критерия vIv и принять статистическое решение. Ошибки первого и второго рода: Ошибка 1-го рода – отклонение правильной нулевой гипотезы. Ошибка 2-го рода – принятие неправильной нулевой гипотезы. Последствия указанных ошибок часто оказывается совершенно различным. Что лучше или хуже – зависит от конкретной постановки задачи и содержания нулевой гипотезы. Принято обозначать а=P(отвергается H0/верна H0) – 1 рода.
|
10.Проверка гипотезы о математическом ожидании нормально распределённой генеральной совокупности при неизвестной дисперсии. Этап 1. Сформулировать Н0 и Н1. Этап 2. Назначить уровень значимости а. Этап 3. Задать объем выборки n. Этап 4. Выбрать статистику vIv критерия и определить распределение статистики vIv при условии что верна H0. T=(xcp-M0)*kor n/S ,эта статистика имеет распределение Стьюдента с n-1 степенью свободы. Этап 5. В зависимости от проверяемой и альтернативной гипотез выбрать область принятия гипотезы и критическую область. Определить критические точки. Критическим значением статистики критерия T будет: tкр=t1-a(n-1) Этап 6. а) Гипотеза Н0 должна быть отвергнута на уровне значимости а, если вычисленное значение tв попадает в критическую область. б) Гипотеза Н0 принимается или её принятие откладывается, если вычисленное tв принадлежит допустимой области. Этап 7. Выполнить эксперимент и проверить гипотезу, т.е. получить выборку намеченного объема вычислить выборочное значение vIv* статистики критерия vIv и принять статистическое решение. T=(xcp-M0)*kor n/S
|

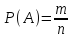 . m
– число благоприятных исходов; n
– число всех исходов.
. m
– число благоприятных исходов; n
– число всех исходов.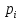 :
0<
:
0<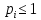 ;
;
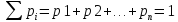
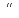
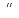
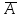 называется противоположным событию
А, если оно наступает тогда и только
тогда, когда не наступает событие А.
называется противоположным событию
А, если оно наступает тогда и только
тогда, когда не наступает событие А.
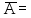 Ω-А
Ω-А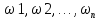 }.
}.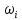 -
элементарный исход,
-
элементарный исход,
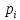 – вероятность эл. исхода
– вероятность эл. исхода
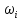 ,
Р(А) – вероятность события А.
,
Р(А) – вероятность события А.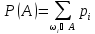
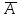 )=1-Р(А)
)=1-Р(А)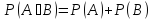

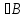 ,
то Р(А)≤Р(В)
,
то Р(А)≤Р(В)
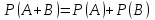
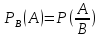 - обозначение условия вероятности.
- обозначение условия вероятности.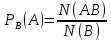 ,
где N(AB)
– число общих элементарных исходов
в событиях А и В, N(B)
– число
элементарных исходов в событии В.
,
где N(AB)
– число общих элементарных исходов
в событиях А и В, N(B)
– число
элементарных исходов в событии В.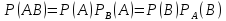 – теорема применяется для зависимых
событий.
– теорема применяется для зависимых
событий.
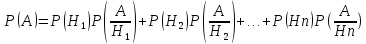
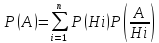 ,
(условная
вероятность события, при гипотезе),
где P(Hi)
– априорная вероятность гипотезы Hi,
,
(условная
вероятность события, при гипотезе),
где P(Hi)
– априорная вероятность гипотезы Hi,
 – условная вероятность события А
при гипотезе Hi.
– условная вероятность события А
при гипотезе Hi.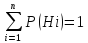
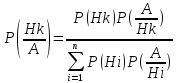
 (противоположное А).
(противоположное А). :
q=1-p;
:
q=1-p;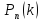 выражается формулой Бернулли:
выражается формулой Бернулли: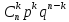 =
=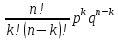

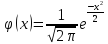 – функция плотности
нормализованного распределения
(Гаусса)
– функция плотности
нормализованного распределения
(Гаусса)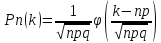
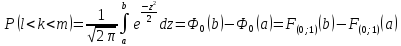
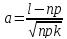 и
и
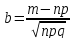
 .
.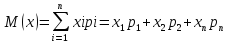
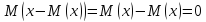
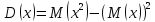
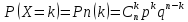 ,
где q=1-p,
k=0,1,2,…,n,
0<p<1.
,
где q=1-p,
k=0,1,2,…,n,
0<p<1.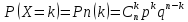 можно рассматривать как общий член
разложения бинома Ньютона:
можно рассматривать как общий член
разложения бинома Ньютона:
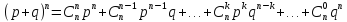
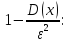
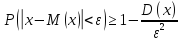
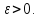
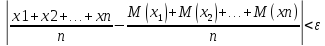 будет как угодно близка к единице,
если число сл. величин достаточно
велико.
будет как угодно близка к единице,
если число сл. величин достаточно
велико.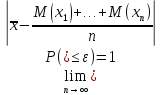
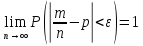
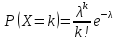 ,
где
,
где
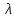 >0
– параметр распределения Пуассона.
е
>0
– параметр распределения Пуассона.
е
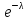
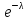
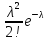
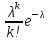
 (0;1),
если Х принимает значения k=1,2,3,…
с вероятностями
(0;1),
если Х принимает значения k=1,2,3,…
с вероятностями

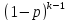
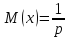 ;
;
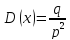

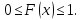 Значения ф-ции
распределения принадлежат отрезку
[0;1]
Значения ф-ции
распределения принадлежат отрезку
[0;1] если
если
 ,
F(x)
– неубывающая функция
,
F(x)
– неубывающая функция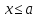 F(x)=1
при
F(x)=1
при
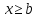 .
.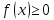 ,
плотность распределения – неотрицательная
функция.
,
плотность распределения – неотрицательная
функция.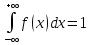 ,
несобственный интеграл от плотности
распределения в пределах от (-∞) до
(+∞) равен единице.
,
несобственный интеграл от плотности
распределения в пределах от (-∞) до
(+∞) равен единице. ,
,
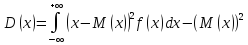
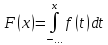 .
Вероятность попадания в интервал
(a;b)
для непрерывной сл. величины выражается
формулой:
.
Вероятность попадания в интервал
(a;b)
для непрерывной сл. величины выражается
формулой:
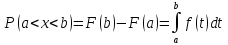
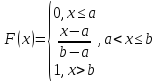 (ГРАФИК)
(ГРАФИК)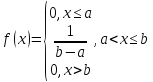 (ГРАФИК)
(ГРАФИК)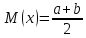 ,
,