5-Дифур

Задача 1. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде

ψ ( x, y) = C).

y¢y

1 - x2

+ 1 =

0.

1 - y 2

y′y

1 − x2

=

− 1,

1 − y 2

dy y

1 − x2

= − 1,

dx

1 − y 2

y

dy = −

dx

,

1 − y 2

1 − x2

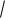− 1 − y 2 = − arcsin x + C, C = arcsin x − 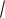1 − y 2 .

Задача 2. Найти общий интеграл дифференциального уравнения.

y′ =	x + 2 y	.
	2x − y

1 + 2

y

y

′

=

x

,

2 −

y

x

Введем замену

y

=

u Þ y = ux Þ y¢ = u + u¢x.

x

u +

x du =

1 + 2u

,

dx

2 − u

x

du

=

1 + u 2

,

dx

2 −

u

2 − u

du =

dx

,

1 + u 2

x

æ

2

u

ö

dx

ò ç

-

÷ du

= ò

x

,

1 + u

2

1 + u

2

è

ø

2arctgu −

1 ln

1 + u 2

= ln

x

+ ln C,

2

y

y 2

2arctg

−

1

ln

1

+

= ln

x

+ ln C.

x

2

x2

Задача 3. Найти общий интеграл дифференциального уравнения.

y′ =	x + 2 y − 3	.
	4x − y − 3

ì	x=	x1 +	k	,
í	y=	y1 +	n
î

y′	=	x1 + 2 y1 + k + 2n − 3
1		4x1 − y1 + 4k − n − 3

ì

k+

2h-

3=

0

í

4k- h-

3=

0

,

î

Пусть ì

k=

1

í

h=

.

î

1

y′

=

x1 +

2 y1

,

1

4x1 − y1

1 + 2

y1

y′

=

x

.

1

1

4 −

y1

x

1

Введем замену

y1

= u Þ

y1 = ux1

Þ

y1¢

= u + u¢x1 .

x1

u + u¢x = 1 + 2u

,

1

4

- u

u¢x

=

1 - 2u + u

2

,

1

4 - u

du

x

=

(1 - u)2

,

dx

4 -

u

1

4 - u

du =

dx1 ,

(u - 1)2

x

1

ò

æ

1 -

u

3

ö

ò

dx

ç

+

÷ du =

1

,

u 2

- 2u +

1

(u - 1)

x

ç

2 ÷

è

ø

1

- 1 ln

u 2 - 2u + 1

-

3

= ln

x

+ C,

2

u

- 1

1

- 1 ln

(u - 1) 2

-

3

= ln

x

+ C,

2

u - 1

1

ö 2

1

æ

y

x

-

ln

ç

1

- 1÷

-

1

= ln

x

+ C,

2

ç

x

÷

y

-

x

1

è

1

ø

1

1

-

1

ln

( y - x) 2

-

x - 1

= ln

x - 1

+ C.

2

(x - 1) 2

y -

x

Задача 4. Найти решение задачи Коши.

y′ − y cos x = 12 sin 2x, y(0) = 0.

y′ + P(x) y = f (x) ,

Пусть y = uv.

Разделим переменные в этом дифференциальном уравнении относительно функции v , находим

v=

e−

òP(x)dx

=

e−ò

cosxdx=e−sinx.

u=

12òsine−sin2xxdx=

12òesinxsin2xdx=

òesinxsinxcosxdx=

sincosxxdx=t=dt

= òetdt=

u=

t

=

dvdu

==

edttdt

=tet−

òetdt=tet−et+

C=

sinxesinx−esinx+

C.

v=

et

y = e− sin x (sin xesin x

- esin x

+ C),

y(0) = 0 Þ 0 = 1× (0 × 1 - 1 + C) Þ C = 1.

y = e− sin x (sin xesin x

- esin x

+ 1).

Задача 5. Решить задачу Коши.

y 2 dx + (xy − 1)dy = 0, y

|x= 1

= e.

y 2

dx

+ ( xy − 1) = 0,

dy

dx

+

x

−

1

= 0.

dy

y

y 2

Пусть x =

uv.

dx

= u¢v + uv¢,

dy

u¢v + uv¢ + uv -

1

= 0,

y 2

y

æ

v

ö

1

uç v¢ +

÷

+ u¢v

-

= 0.

2

ç

y

÷

y

è

ø

Разделим переменные в этом дифференциальном уравнении относительно функции v , находим 1) v′ + vy = 0, dydv = − vy ,

dv = -					dy		, ln v = - ln y Þ v =		1	.
						y
v									y
2) u¢v -						1		= 0,
						2
						y
u¢	1		=			1	,
	y				y 2
du =				1		,
				y
dy
du =			dy ,
				y

u = ln y + C,

x = 1y (ln y + C) -общее решение ДУ. y|x= 1 = e Þ C = e - 1;

x = 1y (ln y + e - 1) -частное решение ДУ.

Задача 6. Найти решение задачи Коши.

3(xy′ + y) = y 2 ln x, y(1) = 3.

	y¢ +	y	=	y2 ln x	.
		x		3x

y = uv,

u′v + uv′ + uv

=

u 2 v2 ln x .

x

3x

1) Пусть

v¢ +

v

=

0,

x

dv

=

-

v

,

dx

x

dv

=

-

dx ,

v

x

1 .

ln v = - ln x Þ v =

x

2) u

¢v =

u 2 v2 ln x

,

x

du

×

1

=

u 2

ln x

,

dx

x

x3

du

=

ln x

dx,

u 2

x2

- 1

= - ln x - 1

+ C,

u

x

x

u =

,

ln x - 1 - Cx

y =

1

,

ln x - 1 - Cx

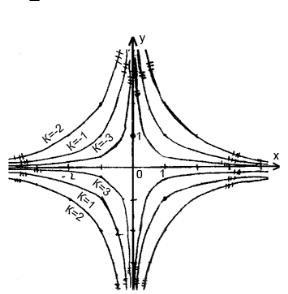
y(1) = 3 Þ C = - 2 / 3.

y =	3	.
	3 ln x + 2x − 3

Задача 7. Найти общий интеграл дифференциального уравнения.

( y 2

+

y sec2

x)dx + (2xy + tgx)dy = 0.

P(x, y) =

y 2

+

y sec2 x,

Q(x, y) =

2xy + tgx,

∂ P

=

2 y + sec 2 x = 2 y +

1

∂ y

cos 2 x,

∂ Q

=

2 y +

1

,

∂ x

cos 2

x

∂ P

=

∂ Q

.

∂ y

∂ x

u(x, y) = ò (2xy + tgx)dy = xy 2 + ytgx + ϕ (x),

	∂ U	= y 2	+ y sec 2 x = y 2 + y sec 2 x + ϕ ′(x).
	∂ x

ϕ ′( x) = 0,

ϕ ( x) = C.

u( x, y) = xy 2 + ytgx = C.

Задача 8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку.

y′ = xy, M (0,1).

y′ = k = const Þ k = xy,

y = kx , т.е. гипербола.

Задача 9. Найти линию, проходящую через точку M 0 , если отрезок любой ее касательной между точкой касания и осью Oy делится на точке пересечения с осью абсцисс в отношении a : b (считая от оси Oy ).

M 0 (1,2), a : b = 2 : 1.

y − y0 = y′(x − x0 ) − уравнение касательной.

( y; x) -координаты произвольной точки, принадлежащие касательной. По условию

BMAB = 12 ,

AOB и BCM подобны.

	AB		=	OB		,
	BM			BC
	xB			=	2	Þ xB = 2x - 2xB Þ x B =	2	x(1).
	x -	xB			1		3

Точка B( xB ;0) принадлежит касательной, поэтому подставим координаты координаты точки B( xB ;0) в

уравнение касательной.

y =

y¢(x - xB ), xB =

x -

y

(2).

y¢

Подставим (1) в (2).

2 x =

x -

y

,

3

y¢

y

=

1 x,

y¢

3

dy

= 3 dx

,

y

x

ln y = 3ln x + ln C Þ y = x3C.

M 0

(1,2) Þ 1 = 2

3 C Þ

C = 1 .

8

Отсюда, y

æ

x ö

3

= ç

÷

- уравнение искомой линии.

è

2 ø

Задача 10. Найти общее решение дифференциального уравнения.

y′′′ctg2x + 2 y′′ = 0.

ì

y′′

=

z(x),

Замена: í

y¢¢¢

=

z¢(x).

î

z′ctg2x + 2z =

0,

z¢ + 2

z

=

0.

ctg2x

Предположим, что z =

uv.

u¢v + uv¢

+ 2

uv

=

0,

ctg 2x

æ

v

ö

u¢v + uç v¢ + 2

÷

= 0.

ç

÷

è

ctg2x ø

Пусть v′ +

2

v

=

0.

ctg2x

dv

= - 2

v

,

dx

ctg 2x

dv

= - 2

dx

,

v

ctg 2x

ln v = ln cos 2x Þ

v = cos 2x.

u¢v = 0,

dudv cos 2x = 0, u = C1 ,

z = C1 cos 2x.

y¢ =	ò	C cos 2xdx =			1 C sin 2x + C .
			1		2	1		2
y =	ò	æ	1	C1 sin 2x +	C2	ö	1	C1 cos 2x + C2 x + C3 .
		ç	2			÷ dx = -	4
		è				ø

Задача 11. Найти решение задачи Коши. y′′ = 72 y3 , y(2) = 1, y′(2) = 6.

			ì	y′	=	z(y),
Замена: í				y¢¢	=	z¢(y)× z(y).
			î
	z¢ z = 72 y 3 ,
	y
	¶z		z = 72 y 3 ,
	¶y
	ò z¶z = 72ò y 3 ¶y,
1 z2			= 18 y4		+	C ,
2						1
z2 =			36 y4 +		2C
						1.

z2 = ( y¢)2 Þ ( y¢)2 = 36 y4 + 2C1 . 36 = 36 + 2C1 Þ C1 = 0.

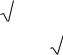
y′ =

36 y 4 ,

y′ =

dy

= 36 y 4 ,

dx

dy

=

ò dx,

6 y 2

ò

1

x + C2 ,

−

6 y

=

y = −

1

.

6( x + C2 )

x = 2, y = 1, 1 = -

1

Þ C2

= -

13 .

6(2

+ C2 )

6

y =

-

1

.

6x - 13

Задача 12. Найти общее решение дифференциального уравнения. y′′′ + 3 y′′ + 2 y′ = 1 − x 2 .

yОН = yОО + yЧН .

λ 3 + 3λ 2 + 2λ = 0 -характеристическое уравнение.

λ 1 = 0, λ 2 = - 1, λ 3 = - 2,

yОО = C1 + C2 + C3 e− x -общее решение однородного уравнения.

yЧН = ( Ax2 + Bx + C)x,

yЧН

= Ax3 + Bx2 + Cx,

y′ = 3Ax3 + Bx2 + C,

y′′ =

6 Ax +

2B,

y′′′ =

6 A,

6 Ax2 + 4Bx + 2C + 18Ax + 6B + 6 A = 1 − x2 ,

6 Ax2 + x(18A + 4B) + 6 A + 6B + 2C = 1 − x2 .

6 A = - 1 Þ A = -

1 ,

6

4

18A + 4B = 0 Þ B =

,

13

6 A + 6B + 2C = 1 Þ C = - 3.

æ

1

2

4

ö

Отсюда yЧН

= xç -

x

+

x -

3÷ - частное решение неоднородного уравнения.

6

3

è

ø

Общее решение

y

OН

= C + C

e− x

+ C

e− 2 x - 1 x3 + 4 x2 - 3x.

1

2

3

6

3

Задача 13. Найти общее решение дифференциального уравнения. y′′′ − 4 y′′ + 5 y′ − 2 y = (16 − 12x)e− x .

yОН = yОО + yЧН .

λ 3 − 4λ 2 + 5λ = 0 -характеристическое уравнение.

λ 1 = 2, λ 2,3 = 1,

yОО = C1e2 x + (C2 + C3 x)ex -общее решение однородного уравнения.

yЧН = ( Ax + B) x2 e− x ,

yЧН = ( Ax3 + Bx2 )e− x ,

y′ = (− Ax3 − Bx2 + 3Ax2 + 2Bx)e− x ,

y′′ = ( Ax3 + Bx2 − 6 Ax2 − 4Bx + 6 Ax + 2B)e− x ,

y′′′ = (− Ax3 − Bx2 + 9 Ax2 + 6Bx − 18 Ax − 6B + 2B)e− x ,

− 10 Ax3 + x2 (48 A − 10B) + x(34B − 42 A) + 6 A − 14B = 16 − 12x.

	- 42 A + 34B = - 12 Þ A =														7	,
														16
											3
	6 A - 14B = 0 Þ B =												.
									16
	Отсюда yЧН =				1	(7 x3					+ 3x2 )e− x - частное решение неоднородного уравнения.
				16
	Общее решение
	y	OН	= C e2 x	+ (C			2	+ C				3	x)ex +				1	(7x3	+ 3x2 )e− x .
			1											16

Задача 14. Найти общее решение дифференциального уравнения.

y′′ + y = 2 cos 7x + 3sin 7x.

yОН	= yОО + yЧН .
λ 2 +	λ	= 0 -характеристическое уравнение.
λ 1 =	0, λ 2 = − 1,
yОО =		C1 + C2 e− x -общее решение однородного уравнения.
yЧН	=	Acos 7x + B sin 7x,
y′ =	− 7 Asin 7x + 7B cos 7 x,
y′′ =	− 49 A cos 7x − 49B sin 7x,

− 49 Acos 7x − 49B sin 7x − 7 Asin 7x + 7B cos 7 x = 2 cos 7x + 3sin 7 x, (7B − 49 A) cos 7x + (− 7 A − 49B) sin 7x = 2 cos 7x + 3sin 7x.

	ì	7B-	49A= 2,
	í	- 7A-		49B = 3
	î
	ì	A=	-	17	,
	ï
				350
	í				.
	ï	B =	-	133
	ï			2450
	î

Отсюда yЧН = − 35017 cos 7x − 2450133 sin 7x - частное решение неоднородного уравнения.

Общее решение

yOН = C1 + C2 e− x − 35017 cos 7x − 2450133 sin 7x.

Задача 15. Найти общее решение дифференциального уравнения. y′′ + y = 2 sin x − 6 cos x + 2e x .

yОН = yОО + yЧН .

λ 2 + λ = 0 -характеристическое уравнение.

λ 1		=	0, λ 2		= − 1,
yОО =				C1 + C2 e− x -общее решение однородного уравнения.
yЧН			=	Acos x + B sin x + Сe x ,
y′ =			− Asin x +					B cos x + Ce x ,
y′′ =			− Acos x −					B sin x +	Ce x ,
−		Acos x − B sin x + Ce x							+ Acos x + B sin x + Ce x = 2 sin x − 6 cos x + 2e x ,
2Ce x = 2 sin x − 6 cos x + 2e x .
2C =			2 Þ		C = 1.
Отсюда yЧН = ex - частное решение неоднородного уравнения.
Общее решение
y	OН		= C + C			2	e− x + ex .
				1
Задача 16. Найти решение задачи Коши.
y′′ +			4 y =		4ctg2x, y(π / 4) = 3, y′(π / 4) = 2.
yОН			= yОО + yЧН .
λ 2		+	4λ	=	0 -характеристическое уравнение.
λ 1		=	0, λ 2		= − 4,
yОО			= C1 + C2 e− 4 x -общее решение однородного уравнения.

ì	u′		y1 +
í	u¢		y1¢ +
î
ì	u	¢	×1+
ï
í		¢
ï	u		× 0+
î

	v′	y2	=	0,		,
	¢	¢
			=	f(x)
	v	y2
	v¢e−		4x	=		0,
	v¢(-		4e−		4x) = 4ctg2x.