
- •Аппроксимация периодического сигнала рядом Фурье.
- •1. Введение
- •2. Теоретическая часть
- •2.1 Представление периодических функций рядом Фурье.
- •2.2. Примеры разложения в ряд Фурье реальных сигналов.
- •2.3. Спектральное представление сигналов.
- •2.4. Спектры последовательности прямоугольных импульсов.
- •2.5. Спектры при уменьшении длительности импульса и периода сигнала.
- •4. Расчетная часть. (выполняется при домашней подготовке)
- •5. Экспериментальная часть.
- •6. Содержание отчета.
- •7. Контрольные вопросы.
Лабораторная работа № 8
Аппроксимация периодического сигнала рядом Фурье.
|
Цель работы: |
Изучение представления различных периодических сигналов рядом ортогональной системе тригонометрических функций
|
1. Введение
В электроэнергетике и электротехнике предъявляются достаточно жёсткие требования к строго синусоидальному закону изменения токов и напряжений во времени. Но во многих областях радиотехники, автоматики, связи, электротехники, несинусоидальные, периодические сигналы (тока и напряжения) соответствуют нормальному режиму работы цепей и устройств. Нередко даже при синусоидальном входном воздействии выходная величина существенно отличается от гармонической, если в цепи содержатся наименьшие элементы (электронные или полупроводниковые приборы, катушки с ферромагнитным сердечником и др.). Поэтому методы анализа цепей с периодическими негармоническими воздействиями имеют большое значение при, разработке устройств весьма широкого применения.
Поскольку разновидностей периодических негармонических сигналов, в принципе, неограниченное множество, важнейшей задачей становится выбор такого метода анализа, который был бы применим к любой форме сигнала. Таковым оказался метод, основанный на использовании тригонометрического ряда Фурье и принципа суперпозиции, применимого к линейным энергетическим цепям.
2. Теоретическая часть
2.1 Представление периодических функций рядом Фурье.
Все периодические сигналы (напряжения, токи), отличаемые от гармонических, называются негармоническими. Они характеризуются периодом Т, формой и размахом напряжения или тока (Up или Ip_). Математически такой сигнал, как функция времени, удовлетворяет условию:
![]()
![]()
![]()
Если эта функция удовлетворяет ряду условий, называемых условиями Дирихле, (в пределах периода Т функция f(x) непрерывна, либо имеет конечное число разрывов первого рода и конечное число максимумов и минимумов), то такая функция может быть представлена в виде бесконечного гармонического ряда Фурье. Сумма этого ряда совпадает со значениями f(t) во всех точках непрерывности, а в точках разрыва дает среднее арифметическое предельных значений функции при приближении к точке разрыва слева f(t-) и справа f(t+).
Если обозначить w=2/Т (частота основной или первой гармоники), то ряд Фурье в тригонометрической форме можно записать:
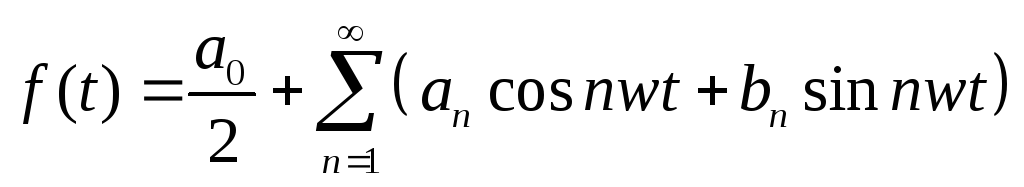 (1)
(1)
где
![]()
 (2)
(2)
![]()
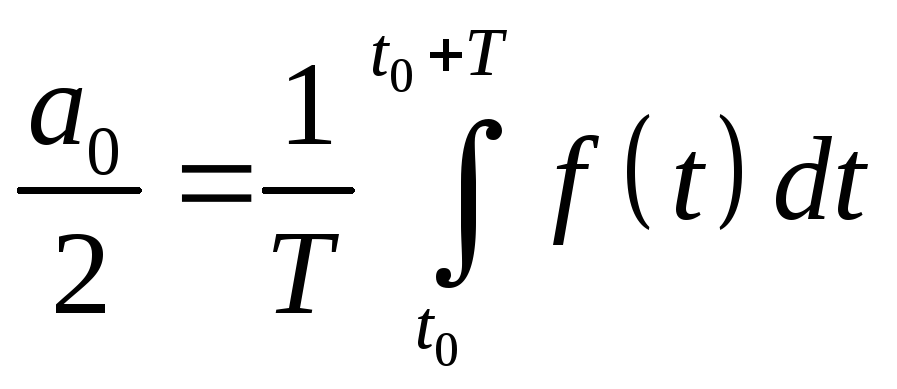
![]() -
постоянная составляющая, an,
вn
- амплитуды
косинусоидальных и синусоидальных
членов ряда. Как следует из (1), ряд Фурье
содержит только кратные основной
частоте гармонические слагаемые,
поскольку n
принимает только целые значения, и
называется номером гармоники. Все
гармоники, кроме первой, называются
высшими
гармониками.
-
постоянная составляющая, an,
вn
- амплитуды
косинусоидальных и синусоидальных
членов ряда. Как следует из (1), ряд Фурье
содержит только кратные основной
частоте гармонические слагаемые,
поскольку n
принимает только целые значения, и
называется номером гармоники. Все
гармоники, кроме первой, называются
высшими
гармониками.
Можно
показать, что значения an
и
вn
не зависят
от выбора t0.
Поэтому, положив t0.=0.
Поэтому, положив t0.=0
и введя новую переменную
![]() с учетом, что
с учетом, что![]() и
и![]() ,
формулы (1) и (2) можно переписать:
,
формулы (1) и (2) можно переписать:
![]() (3)
(3)
![]() (4).
(4).
Если вспомнить соотношение из тригонометрии:
![]() (5)
(5)
о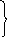 ткуда
ткуда![]() и
и
(6)
![]() ,
,
то ряд Фурье запишется в виде:
![]() .
(7)
.
(7)
либо
![]() ,
(8)
,
(8)
где
![]() (9)
(9)
Очень часто периодические функции электрических или магнитных величин обладают некоторым видом симметрии, что значительно укрощает разложение такой функции в ряд Фурье. Отметим некоторые виды симметрии:
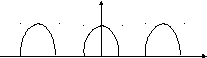
1. Функция f() симметрична относительно оси ординат (рис.1).
 f()
f()

 t
t
-2
Рис. 1.
В
этом случае
![]() ,
т.е. функциячетная.
Из тригонометрических функций четной
является только косинус, а синус –
нечетная. Поэтому синусоиды не входят
в состав ряда Фурье таких функций, т.е.
,
т.е. функциячетная.
Из тригонометрических функций четной
является только косинус, а синус –
нечетная. Поэтому синусоиды не входят
в состав ряда Фурье таких функций, т.е.
![]() , (10)
, (10)
т.е. четная функция может содержать только косинусоиды и постоянную составляющую. Важное свойство четных функций: для определения коэффициентов аn достаточно пользоваться кривой f() за половину периода, т.е.
![]() (11)
(11)
 2.
Функция f()
симметрична относительно начала
координат
(рис.2).
2.
Функция f()
симметрична относительно начала
координат
(рис.2).
f()






 0
0
2


Рис. 2
В этом случае выполняется условие f(-)= -f(). Такие функции называются нечетными. Этому условию не удовлетворяют постоянная составляющая и косинусоиды, поэтому при данном виде симметрии ряд содержит только синусоиды.
![]() , (12)
, (12)
т.е. нечетная функция может содержать только синусоиды. Здесь также для определения коэффициентов bn достаточно пользоваться кривой f() за половину периода, т.е.
![]() (13)
(13)
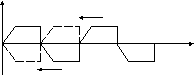
3. Функция f() симметрична относительно оси абсцисс, если её дополнить той же функцией, смещенной на полпериода (рис. 3).
Такая функция удовлетворяет условию: f()= -f(+). Заменив f() по формуле (3), получим:
![]() ,
,
откуда для четных n получим:
![]() .
.
Это условие выполняется при произвольных значениях только в том случае, когда a0=0 и an=bn=0 для четных n. То есть, при данном виде симметрии
![]() . (14)
. (14)
Поэтому, функция с данным видом симметрии содержит только нечетные гармоники. Коэффициенты an и bn можно вычислять по формулам (11) и (13).
2
Рис. 3
При разложении периодической функции в ряд Фурье следует сначала проанализировать её на наличие каких-либо видов симметрии. Если они имеются, то этот факт позволяет предсказать, какие гармоники не войдут в разложение. Если, например, одновременно выполняются условия симметрии по п.п. 1 и 3, то в разложении будут только нечетные синусоиды.
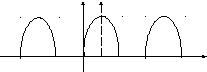
Часто для придания функции симметрии относительно оси ординат бывает необходимо перенести начало отсчета. На рис. 4 показана однополупериодная синусоида. Если сместить начало отсчета на отрезок , то кривая становится симметричной относительно оси абсцисс.
 f()
f()
 0 0’
0 0’
Рис. 4.
Пусть для некоторой функции f() известно разложение в ряд Фурье, т.е. заданы коэффициенты an и bn:
![]() .
.
Если сместить начало отсчета на отрезок вправо или налево относительно исходного положения, то разложение функции в новой координатной системе получается заменой на 1 +1, где 1 – абсцисса в новой системе координат; >0 – соответствует смещению нового начала координат вправо, <0 – влево.
![]() (15)
(15)
Используя известные соотношения для тригонометрических функций:
![]() ,
,
выражение под знаком суммы формулы (3) можно переписать:
![]()
Из
формул (4) нетрудно определить, что an
– четная функция n,
а bn
– нечетная, т.е. an=a-n;
bn=
-b-n.
Кроме того,
![]() .
.
Поэтому ряд Фурье можно записать в следующем виде:
![]()
![]() , (16)
, (16)
где
![]() (17)
(17)
называется комплексной амплитудой n-ой гармоники. Формула (16) – ряд Фурье в комплексной форме.
