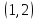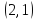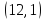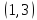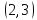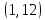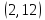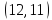Zanyatie_1
.docxТеория.
Тема урока: Элементы комбинаторики. Правило сложения и умножения.
Комбинаторика (или теория соединений) – это раздел алгебры, в котором изучаются некоторые операции над конечными множествами и решаются задачи, связанные с этими операциями.
Задача №1. В соревнованиях участвуют 8 команд. Сколько существует вариантов распределения мест между этими командами?
Решение.
Условно обозначим все команды цифрами: 1, 2, 3, 4, 5, 6, 7, 8. Тогда, возможны например, такие варианты распределения мест: (1, 2, 3, 4, 5, 6, 7, 8); (1, 3, 5, 7, 2, 4, 6, 8); (6, 7, 8, 5, 4, 3, 2, 1).
Кроме этих вариантов существуют и другие. Очевидно, всех возможных вариантов будет столько, сколько существует различных перестановок из восьми цифр. При этом перестановки естественно считать разными, если хотя бы на одном месте они содержат разные цифры.
Задача №2. В полуфинальном турнире участвуют восемь команд: 1, 2, 3, 4, 5, 6, 7, 8. В финал попадают лишь три из них. Сколько существует различных вариантов выхода команд в финал?
Решение.
Может оказаться, что в финал попадут команды 2, 4 и 5, а может быть 2, 6 и 8, или другие три команды. Возможных вариантов выхода команд в финал будет столько, сколько существует способов выбора трех цифр из восьми. При этом порядок расположения этих трёх цифр не играет никакой роли.
Задача №3. Пусть по – прежнему соревнуются 8 команд, но турнир финальный. Разыгрываются три медали: золотая, серебряная и бронзовая. Сколько существует различных вариантов распределения медалей?
Решение.
Рассмотрим возможные варианты выбора трёх команд из восьми. Будем учитывать то, какие команды окажутся на первых трёх местах, и то, как они поделят эти места между собой. Поэтому распределение мест (5, 2, 4) и (4, 5, 2) рассматриваются как два различных результата.
Общая схема этих
задач такова.
Имеется некоторое множество, содержащее
 элементов (в задачах
элементов (в задачах
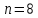 ).
Из этих элементов составляются различные
комбинации, которые можно различать
как по составу,
так и по
порядку
расположения элементов.
).
Из этих элементов составляются различные
комбинации, которые можно различать
как по составу,
так и по
порядку
расположения элементов.
В задаче 1 тип
комбинаций характеризуется тем, что в
каждую комбинацию входят все данные
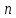 элементов; в этом случае одна комбинация
от другой отличается порядком следования
элементов. Комбинации подобного типа
называют перестановками
(в данном
случае мы имели перестановки из 8
элементов).
элементов; в этом случае одна комбинация
от другой отличается порядком следования
элементов. Комбинации подобного типа
называют перестановками
(в данном
случае мы имели перестановки из 8
элементов).
В задаче 2 описаны
комбинации, каждая из которых состоит
из
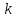 элементов, взятых из данных
элементов, взятых из данных
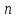 элементов, и отличающиеся одна от другой
лишь составом. Порядок расположения
элементов в таких комбинациях не
существенен. Подобного типа комбинации
называются сочетаниями
(в примере
2 – сочетания из 8 элементов по 3).
элементов, и отличающиеся одна от другой
лишь составом. Порядок расположения
элементов в таких комбинациях не
существенен. Подобного типа комбинации
называются сочетаниями
(в примере
2 – сочетания из 8 элементов по 3).
В задаче 3 описаны
комбинации, которые состоят из
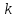 элементов, взятых из данных
элементов, взятых из данных
 элементов, и отличающиеся одна от другой
либо составом,
либо порядком
расположения элементов. Такие комбинации
называют размещениями
(в примере
3 – размещения из 8 элементов по 3).
элементов, и отличающиеся одна от другой
либо составом,
либо порядком
расположения элементов. Такие комбинации
называют размещениями
(в примере
3 – размещения из 8 элементов по 3).
Правило суммы.
Если в нашем
распоряжении
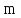 способов выбора элемента
способов выбора элемента
 и независимо
от них
и независимо
от них
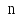 способов выбора элемента
способов выбора элемента
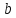 ,
то выбор
,
то выбор
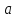 и
и
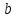 можно сделать
можно сделать
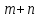 способами.
способами.
Например. В
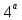 классе 5 отличников, а в
классе 5 отличников, а в
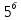 классе 7 отличников. Выбор одного ученика
– отличника для поездки по туристической
путёвке можно сделать
классе 7 отличников. Выбор одного ученика
– отличника для поездки по туристической
путёвке можно сделать
 способами.
способами.
Теорема 1. Если
пересечение конечных множеств
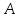 и
и
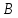 пусто,
пусто,
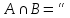 ,
то число элементов в их объединении
равно сумме числа элементов множеств
,
то число элементов в их объединении
равно сумме числа элементов множеств
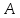 и
и
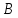 .
.
Примечание.
При использовании правила суммы нужно
следить, чтобы ни один из способов выбора
объекта
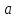 не совпал с каким – нибудь способом
выбора объекта
не совпал с каким – нибудь способом
выбора объекта
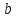 .
Если такие совпадения имеются, то правило
суммы утрачивает силу, получим
.
Если такие совпадения имеются, то правило
суммы утрачивает силу, получим
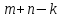 способов выбора, где
способов выбора, где
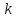 – число совпадений выбора объектов
– число совпадений выбора объектов
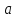 и
и
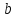 .
.
Пример. В классе 15 учеников участвуют в кружке художественной самодеятельности и 12 – в спортивной секции. Из них 5 – участвуют в обоих кружках. Сколькими способами можно выбрать одного кружковца для направления его по туристической путёвке?
Число возможных
выборов:
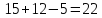 .
.
Теорема 2. Для
любых конечных множеств
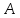 и
и
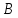 верно равенство
верно равенство
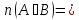
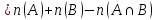 .
.
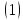
Следствие 1. Если
конечные множества
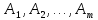 попарно не пересекаются, то есть если
попарно не пересекаются, то есть если
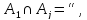 при
при
 ,
то имеет место равенство
,
то имеет место равенство
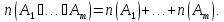
Формула включений и исключений.
Формула включений и исключений является обобщением формулы (1).
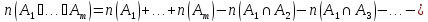
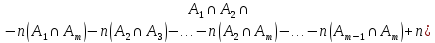
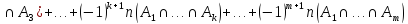 .
(2)
.
(2)
Например, при
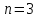 имеем:
имеем:
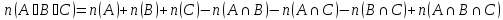 .
.
Правило произведения.
Если в нашем
распоряжении
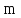 способов выбора элемента
способов выбора элемента
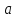 и независимо от них
и независимо от них
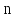 способов выбора элемента
способов выбора элемента
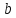 ,
то пару
,
то пару
 можно выбрать
можно выбрать
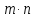 способами.
способами.
Действительно,
пусть все способы выбора элемента
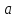 :
:
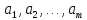 ,
а все способы выбора элемента
,
а все способы выбора элемента
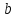 :
:
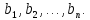
Тогда все пары,
которые можно составить из этих элементов,
можно расположить в следующую таблицу
из
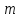 строк и
строк и
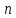 столбцов.
столбцов.
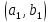
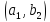 …
…
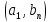
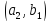
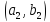 …
…
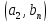
… … … …
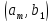
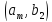 …
…
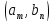
Каждый
из
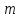 способов выбора элемента
способов выбора элемента
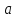 можно скомбинировать с любым
из
можно скомбинировать с любым
из
 способов выбора элемента
способов выбора элемента
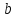 .
Всего в этой таблице
.
Всего в этой таблице
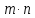 пар.
пар.
Заметим, что иногда
выбор бывает более сложным – надо
сначала выбрать элемент
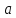 ,
а потом, в зависимости
от этого выбора, элемент
,
а потом, в зависимости
от этого выбора, элемент
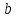 .
Но если элемент
.
Но если элемент
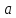 можно выбрать
можно выбрать
 способами, то число различных пар
способами, то число различных пар
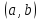 опять равно
опять равно
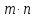 .
.
Пример. В отделении 12 солдат. Каким числом способов можно составить наряд из двух человек, если один из них должен быть назначен старшим?
Решение.
Задача сводится
к выбору пары
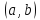 ,
где
,
где
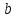 выбирается в зависимости от выбора
выбирается в зависимости от выбора
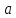 .
Если назначить сначала старшего по
наряду, то для его выбора у нас имеется
12 различных возможностей, то есть
.
Если назначить сначала старшего по
наряду, то для его выбора у нас имеется
12 различных возможностей, то есть
 ,
ибо каждый солдат может быть назначен
старшим наряда. Далее к выбранному
присоединяется один солдат из оставшихся
11 – ти. Возможные варианты представлены
в таблице из 12 строк и 11 столбцов:
,
ибо каждый солдат может быть назначен
старшим наряда. Далее к выбранному
присоединяется один солдат из оставшихся
11 – ти. Возможные варианты представлены
в таблице из 12 строк и 11 столбцов:
|
|
|
… |
|
|
|
|
… |
|
|
… |
… |
… |
… |
|
|
|
… |
|
По правилу
произведения общее число нарядов равно
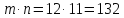 .
.
Пример. Сколько членов в автоклубе, если известно, что при замене номеров машин использованы все трехзначные номера, составленные из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9?
Решение.
Число участников равно числу трехзначных номеров, составленных из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. В данном случае:
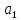 – первую цифру
можно выбрать
– первую цифру
можно выбрать
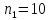 способами,
способами,
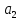 – вторую цифру
можно выбрать
– вторую цифру
можно выбрать
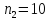 способами,
способами,
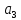 – третью цифру
можно выбрать
– третью цифру
можно выбрать
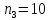 способами.
способами.
Набор трех цифр
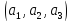 можно выбрать
можно выбрать
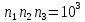 способами, где
способами, где
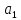 ,
,
 и
и
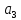 – любая из данных цифр 0, 1, 2, 3, 4, 5, 6, 7, 8,
9.
– любая из данных цифр 0, 1, 2, 3, 4, 5, 6, 7, 8,
9.
Теорема 3. Если
множества
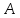 и
и
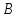 конечны, то числа пар в их декартовом
произведении
конечны, то числа пар в их декартовом
произведении
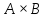 равно произведению числа элементов
этих множеств:
равно произведению числа элементов
этих множеств:
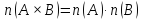 .
.
Теорема 4.
Если множества
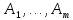 конечны, то имеет место равенство
конечны, то имеет место равенство
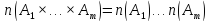 .
.