
Архив2 / курсач docx180 / KURSACh(196)
.docx
1Кинематика плоского движения твердого тела
Условие: ОL=25 см; KH=22см; α=50°;β=10°; εOK=3,1c-2; υK=10см/с.
Рисунок 1- кинематический механизм
Найти:скорости υL, υH, ωKLи ускорения aL,aH,aK, εKL.
Решение:Механизм представляет собой кривошипно-шатунный механизм
Кривошип совершает замедленное вращательное движение с угловой скоростью ωOK и угловым ускорением εОК относительно точки О (рисунок 5).
Скорость и ускорение точки К равны [2]
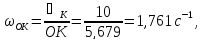
OK находим по теореме синусов
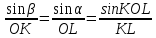
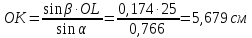
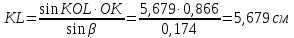
где
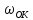 – угловая скорость звена OK,с-1;
– угловая скорость звена OK,с-1;
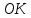 – длина звена ОК,
см.
– длина звена ОК,
см.
Определим ускорение точки К. В векторной форме оно находится по формуле вида
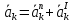 ,
,
где
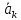 -
вектор ускорения точки К,
-
вектор ускорения точки К,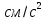 ;
;
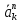 – нормальная
составляющая вектора ускорения точки
К, см/c2;
– нормальная
составляющая вектора ускорения точки
К, см/c2;
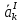 - тангенциальная
составляющая вектора ускорения точки
К, см/c2.
- тангенциальная
составляющая вектора ускорения точки
К, см/c2.
Нормальное ускорение найдём по формуле
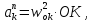
где
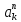 -
нормальное ускорение точки К,
-
нормальное ускорение точки К,
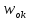 - угловая скорость
звена ОК, с-1.
- угловая скорость
звена ОК, с-1.
После подстановки получим
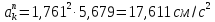 .
.
Тангенциальное ускорение найдём по формуле
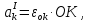
где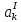 - тангенциальное ускорение точки К,см/c2;
- тангенциальное ускорение точки К,см/c2;
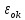 – угловое ускорение
звена ОК, с-2.
– угловое ускорение
звена ОК, с-2.
После подстановки получим:
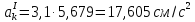 .
.
Ускорение точки К в скалярной форме найдём по формуле:
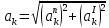 .
.
После подстановки получим:
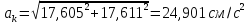 .
.
Рисунок 2– Скорость и ускорение точки К
Шатун KLсовершает плоское движение. Точка Lпринадлежит ползуну L, который совершает движение поступательно. Скорости точек Kи Lне параллельны, следовательно, мгновенный центр скоростей P звена KLлежит на пересечении прямы, перпендикулярных скоростям точек KиL(рисунок 6). Согласно следствию к теореме Шаля имеем
Рисунок 3- определение скоростей точек H,L
где υK- скорость точки К,см/с;
υL- скорость точки L,см/с;
υH- скорость точки H,см/с
KP–длина от точкиK до МЦС - точки P, см;
LP -длина от точкиL до МЦС - точки P,см.
HP -длина от точкиH до МЦС - точки P,см.
Составим пропорцию вида
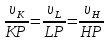
Для нахождения HPвыполним следующие действия
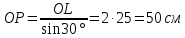
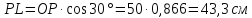
Длину HP определим из треугольника HLP по теореме косинусов. Тогда получим выражение:
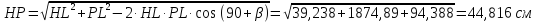
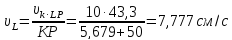
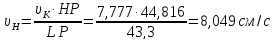
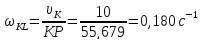
Для нахождения ускорения точки Lвоспользуемся теоремой о сложении ускорений плоской фигуры, где в качестве полюса выберем точку K
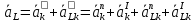
где
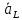 – вектор ускоренияточки L,
см/c2;
– вектор ускоренияточки L,
см/c2;
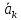 – вектор
ускоренияточки K, см/c2;
– вектор
ускоренияточки K, см/c2;
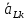 – вектор ускорения
звена KL, см/c2;
– вектор ускорения
звена KL, см/c2;
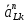 – нормальная
составляющая вектора ускорения звена
KL, см/c2;
– нормальная
составляющая вектора ускорения звена
KL, см/c2;
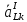 -
тангенциальная составляющая вектора
ускорения звена KL, см/c2.
-
тангенциальная составляющая вектора
ускорения звена KL, см/c2.
Где
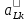 -
ускорение точки Lв
относительном вращении стержня LKвокруг
полюса K(рисунок 7).
Спроецируем векторное равенство на оси
декартовой системы координат xLy,
учитывая что
-
ускорение точки Lв
относительном вращении стержня LKвокруг
полюса K(рисунок 7).
Спроецируем векторное равенство на оси
декартовой системы координат xLy,
учитывая что
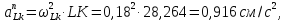
Рисунок 4- определение ускорений точки L
Получим
систему линейных уравнений 2-ого порядка
относительно
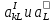
-
На ось ОХ :
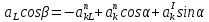
-
На ось OY:
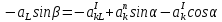
Из 1-ого :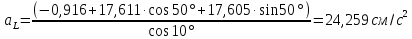
Из 2-ого :
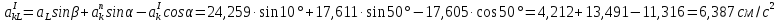
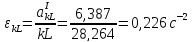
Аналогично находим ускорение точки H
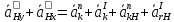
Где
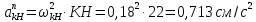
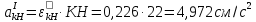
Рисунок 5- определение ускорения точки H
Наось
x:
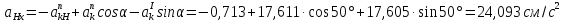
На
осьy:
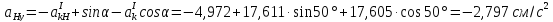
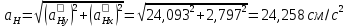 .
.
В
результате расчётов, получили скорости
и ускорения, равные: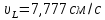 ,
,
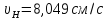 ,
,
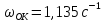 ,
,
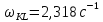 ,
,
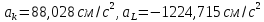 ,
,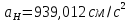 ,
,
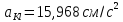 .
.
-
Динамика механической системы
Дано:
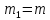 ;
;
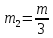 ;
;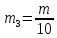 ;
;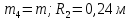 ;
;
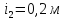 ;
;
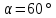 ;
;
;
;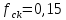 ;;
;;
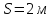 .
Определить скорость центра масс тела
1 в тот момент времени, когда он переместится
на расстояние S, и ускорение
центра масс тела 1.
.
Определить скорость центра масс тела
1 в тот момент времени, когда он переместится
на расстояние S, и ускорение
центра масс тела 1.
Механическая система движется под действием сил тяжести первого тела. Массами нитей пренебречь. Силы сопротивления в подшипниках не учитывать. Диск (каток, колесо) считать сплошным однородным телом, если радиус инерции для него не задан. Все тела в системе абсолютно твердые. Нити нерастяжимые.
Задачу решить тремя способами:
- по теореме об изменении кинетической энергии системы. Проверить результаты расчета кинетической энергии отдельных тел и всей системы, а также работ внешних сил и моментов сил на компьютере в вычислительной лаборатории на кафедре теоретической механики;
- по общему уравнению динамики;
-по уравнению Лагранжа. Провести сравнение коэффициентов в выражении кинетической энергии отдельных тел системы с коэффициентами в выражениях работы сил и моментов сил инерции этих тел соответственно.
Решим задачу по теореме об изменении кинетической энергии. Схема для решения представлена на рисунке 6
Рисунок 6 – Схема для решения задачи по теореме об изменении кинетической энергии
Для начала найдем радиусr2. Он будет равен:
r2=4/5·R2=0,8·0,24=0,192см.
Запишем теорему об изменении кинетической энергии системы:
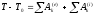 ,
,
где
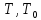 - кинетическая энергия системы в конце
и в начале перемещения центра масс тела
1 из состояния покоя на расстояние S;
- кинетическая энергия системы в конце
и в начале перемещения центра масс тела
1 из состояния покоя на расстояние S;
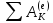 - сумма работ всех
внешних сил и моментов сил на том же
перемещении;
- сумма работ всех
внешних сил и моментов сил на том же
перемещении;
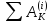 - сумма работ
внутренних сил и моментов сил на
рассматриваемом перемещении системы.
- сумма работ
внутренних сил и моментов сил на
рассматриваемом перемещении системы.
T0
= 0; т.к. система движется из состояния
покоя.
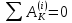 так
как тела в системе абсолютно твердые и
отсутствует относительное движение
тел в системе (нити нерастяжимые, качение
тел по поверхностям и нитям без
скольжения).
так
как тела в системе абсолютно твердые и
отсутствует относительное движение
тел в системе (нити нерастяжимые, качение
тел по поверхностям и нитям без
скольжения).
Определим кинетическую энергию системы. Она получается из суммы кинетических энергий её частей. Тогда получим выражение:
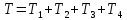
Кинематический расчет для каждого тела:
-
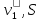
-
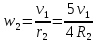
-
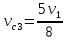 ,
,
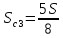 ,
,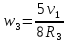 ,
,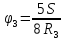
-
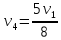 ,
,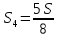
Тело 1 движется поступательно. Тогда его кинетическая энергия будет равна:
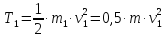 ,
,
где
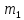 - масса тела 1;
- масса тела 1;
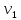 - скорость тела
1.
- скорость тела
1.
Тело 2 вращается. Тогда его кинетическую энергию найдём из выражения:
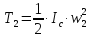 ,
,
где
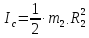 – момент инерции;
– момент инерции;
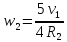 –
угловая скорость.
–
угловая скорость.
Преобразуя формулу, получим:
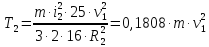
Тело 3 движется плоскопараллельно. Его кинетическая энергия складывается из кинетической энергии вращения и поступательного движения. Тогда получим выражение:
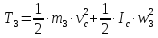
где
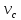 – скорость центра масс;
– скорость центра масс;
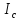 - момент инерции
тела относительно оси, проходящей через
центр масс С перпендикулярно плоскости
тела;
- момент инерции
тела относительно оси, проходящей через
центр масс С перпендикулярно плоскости
тела;
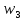 – угловая скорость
тела.
– угловая скорость
тела.
Скорость центра масс:
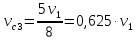
Момент инерции тела выражается формулой:
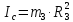
Тогда, после преобразований, формула для нахождения кинетической энергии третьего тела примет вид:
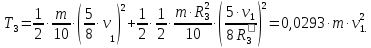
Скорость центра масс:

Тогда, после преобразований, формула для нахождения кинетической энергии четвертого тела примет вид:
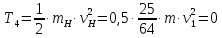 ,1953
,1953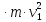
После того, как мы нашли значения всех четырех частей системы, подставим их в формулу для нахождения кинетической энергии системы. Тогда получим выражение:
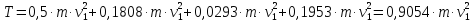
Далее найдём сумму работ внешних сил. Она находится из выражения:
∑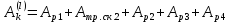 ,
,
где
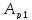 -
работа силы тяжести тела 1;
-
работа силы тяжести тела 1;
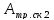 - работа силы трения
скольжения тела 2;
- работа силы трения
скольжения тела 2;
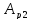 -
работа силы тяжести тела 2;
-
работа силы тяжести тела 2;
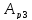 -
работа силы тяжести тела 3;
-
работа силы тяжести тела 3;
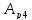 -
работа силы тяжести тела 4.
-
работа силы тяжести тела 4.
.
Работу силы тяжести тела 1 вычислим по формуле:
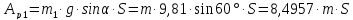
Работа будет положительной, потому что тело 1 опускается.
Работу силы трения скольжения тела 1 вычислим по формуле:
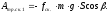
После подстановки известных значений получим:
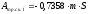 .(2.18)
.(2.18)
Так как точка приложения силы не перемещается, работа силы тяжести тела 2 будет равна нулю:
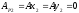
Работу силы тяжести тела 3 вычислим по формуле:
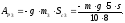
После подстановки значений получим:
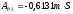
Работу силы тяжести тела 3 вычислим по формуле:
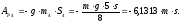
Зная все работы, найдем сумму работ внешних сил, подставив значения. Тогда получим:
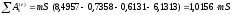
Далее найдём скорость тела 1.
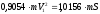 .
.
Сократим массы, выразим скорость и найдём её:
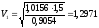 м/c
м/c
Теперь найдем ускорение тела 1. Для этого продифференцируем по времени:
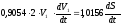
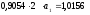
Выразим и найдём ускорение:
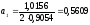 м/c2.
м/c2.
Теперь решим задачу по общему уравнению динамики. Общее уравнение динамики составляется в результате последовательного применения принципа Даламбера для системы и принципа возможных перемещений. Оно записывается в виде равной нулю суммы работ трех групп сил: активных, реакций связей и сил инерции на любом возможном перемещении, задаваемом из положения системы в рассматриваемый момент времени:
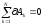
или
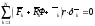
где
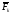 -
активная сила, действующая на k-тую
точку системы;
-
активная сила, действующая на k-тую
точку системы;
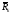 -
реакция связей, приложенная к k-той
точке;
-
реакция связей, приложенная к k-той
точке;
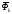 -
сила инерции k-той
точки;
-
сила инерции k-той
точки;
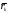 -
радиус-вектор k-той
точки относительно начала координат
-
радиус-вектор k-той
точки относительно начала координат
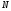 -
число точек системы.
-
число точек системы.
Число независимых общих уравнений динамики для системы равно числу степеней свободы системы.
Механическая система состоит из бесконечного числа точек, поэтому имеет и бесконечное число сил инерции этих точек. Необходимо привести силы инерции к выбранному центру и получить одну силу, равную главному вектору сил инерции, и одну пару сил, векторный момент которой равен главному моменту сил инерции относительно выбранного центра приведения .В динамике за центр приведения чаще всего выбирают центр масс. Главный вектор Ф сил инерции не зависит от центра приведения и всегда вычисляется по формуле:
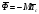 ,
,
где
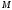 -
масса всей системы;
-
масса всей системы;
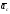 -
вектор ускорения центра масс системы.
-
вектор ускорения центра масс системы.
Главный момент
сил инерции
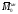 относительно
центра приведения 0 вычисляется по
проекциям на оси координат
относительно
центра приведения 0 вычисляется по
проекциям на оси координат
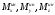 .
.
При поступательном движении тела центр приведения выбираем в центре масс С и имеем
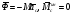 .
.
Во вращательном движении, если выполняются два условия:
-
тело имеет плоскость симметрии, перпендикулярную оси вращения;
-
центр приведения выбирается в этой плоскости симметрии, то главный момент сил инерции параллелен оси вращения и вычисляется по одной проекции на эту ось:
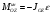 ,
,
гдеО - центр приведения;
Jоz - момент инерции относительно оси, проходящей через центр приведения О и параллельной оси вращения Z;
ε - угловое ускорение тела.
Можно выбирать любую точку за центр приведения, но в большинстве задач динамики рекомендуется выбирать центр масс С за центр приведения, так как решение задач получается более простым, при этом главный вектор сил инерции по-прежнему вычисляется по формуле
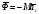 ,
,
а момент сил инерции относительно точки С при выполнении указанных выше двух условий вычисляется по формуле
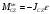 ,
,
где С - центр приведения и центр масс тела;
Jcz - момент инерции тела относительно оси СZ;
ε- угловое ускорение тела.
В
плоском движении за центр приведения
выбирается центр масс. Тело, если нет
особых указаний, имеет плоскость
симметрии, перпендикулярную оси вращения
и проходящую через центр масс, поэтому
надо использовать
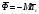 и
и
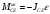 .
.
В моей задаче ,если задержать тело 1, которое движется поступательно и прямолинейно, то есть если убрать одну степень свободы у системы, то вся система остановится. Следовательно, при движении эта система имеет одну степень свободы. Схема для расчёта представлена на рисунке 7
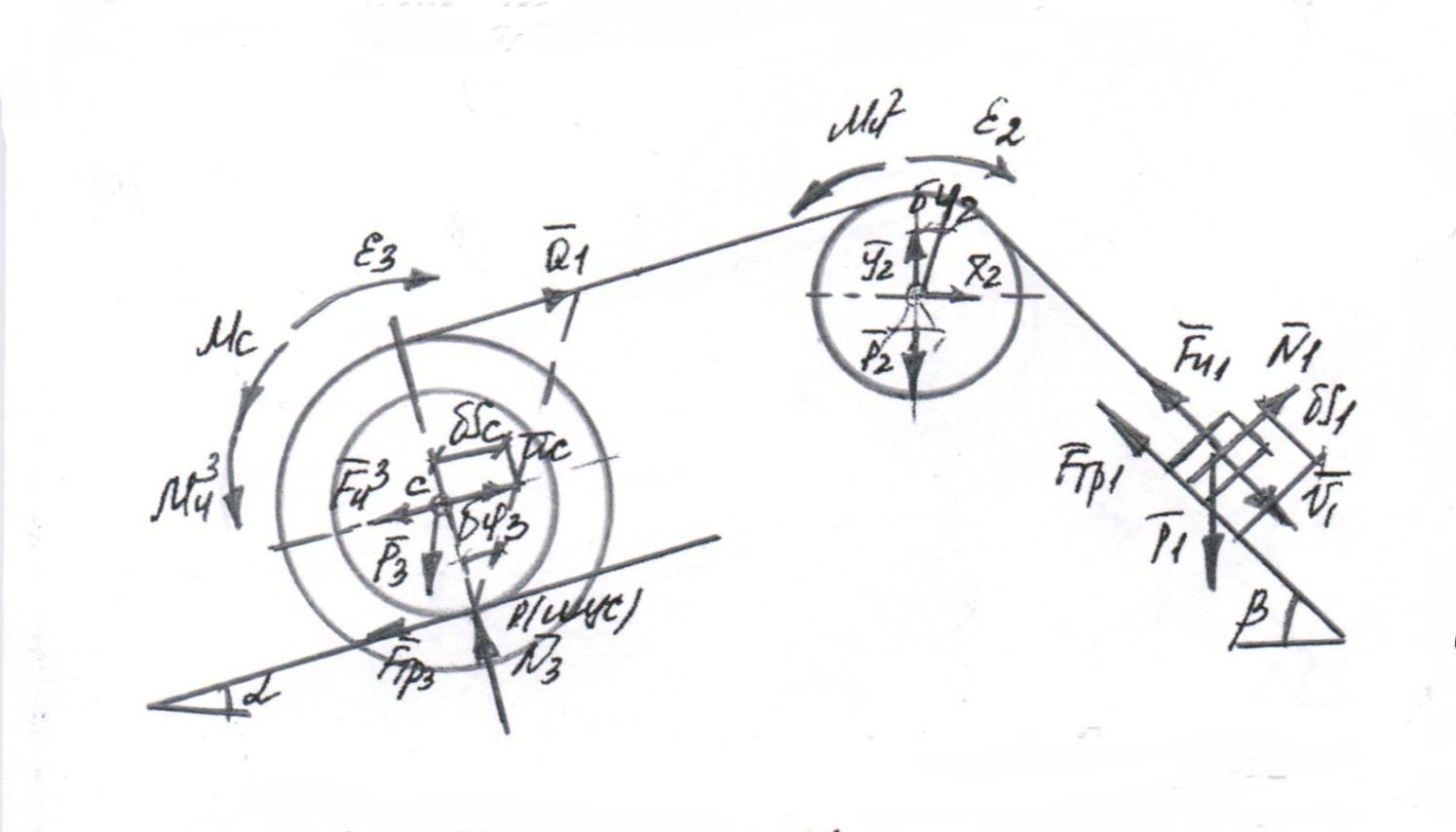
Рисунок 7 – Схема для решения задачи по общему уравнению динамики
Рассмотрим силы действующие на тела. На тело 1 действует сила тяжести:
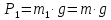
Сила инерции:
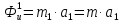
Сила трения:
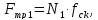 (2.41)
(2.41)
где
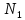 =
=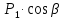 .
.
Подставив значения, получим выражение:
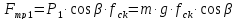 .(2.42)
.(2.42)
На тело 2 действует момент инерции
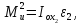 (2.43)
(2.43)
где
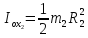 ;
;
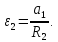
После подстановки значений получим:
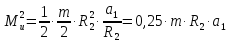 .(2.44)
.(2.44)
На тело 3 действует сила тяжести:
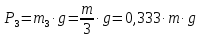 .(2.45)
.(2.45)
Сила инерции:
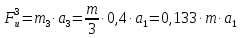 .(2.46)
.(2.46)
Запишем выражение:
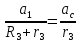 .(2.47)
.(2.47)
Отсюда выразим ускорение центра масс и подставим значения. Тогда получим:
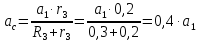 .(2.48)
.(2.48)
Момент инерции центра масс найдём по формуле:
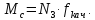 (2.49)
(2.49)
После подстановки получим выражение:
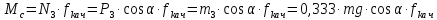 .(2.50)
.(2.50)
Момент инерции найдём по формуле:
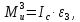 (2.51)
(2.51)
где
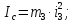
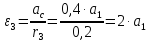 .
.
После подстановки значений получим выражение вида:
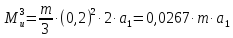 .(2.52)
.(2.52)
Теперь запишем общее уравнение динамики для данной системы. Получим выражение вида:
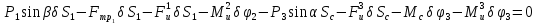 .
(2.53)
.
(2.53)
где
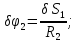
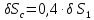 ;
;
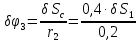 =2
=2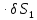 .
.
После подстановки значений получим:
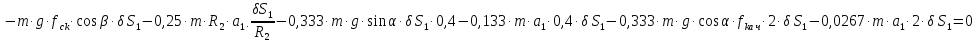 .(2.54)
.(2.54)
Далее
сократим наm,
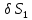 и
и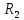 .
Так же подставим числовые значения.Получим
выражение:
.
Так же подставим числовые значения.Получим
выражение:
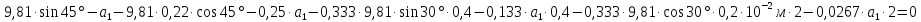 .(2.55)
.(2.55)
После операций с числами получим:
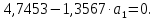 (2.56)
(2.56)
Тогда
ускорение
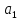 будет равно:
будет равно:
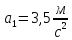 .
.
Наконец, решим задачу по уравнению Лагранжа второго рода. Уравнения Лагранжа второго рода являются дифференциальными уравнениями движения механической системы в обобщенных координатах:
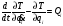
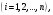 (2.57)
(2.57)
гдеТ - кинетическая энергия системы в абсолютном движении, выраженная в обобщенных координатах;
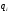 -
i-я
обобщенная координата;
-
i-я
обобщенная координата;
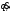 - i-я
обобщенная скорость;
- i-я
обобщенная скорость;
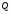 -
обобщенная сила по i-й
обобщенной координате;
-
обобщенная сила по i-й
обобщенной координате;
n - число степеней свободы системы.
Эти уравнения являются дифференциальными уравнениями второго порядка относительно обобщенных координат, дифференциальными уравнениями первого порядка относительно обобщенных скоростей и алгебраическими линейными уравнениями относительно обобщенных ускорений.
Уравнения Лагранжа можно получить из общего уравнения динамики системы, переходя в последнем к обобщенным координатам.
Число независимых уравнений Лагранжа равно числу степеней свободы механической системы.
Поскольку в общем уравнении динамики содержатся работы трех групп сил: активных, реакций связей и сил инерции, а правая часть уравнения Лагранжа представляет собой обобщенную силу, которая рассчитывается через работы только двух групп сил: активных и реактивных связей, то, следовательно, работы сил инерции записаны в левой части уравнения Лагранжа в виде:
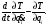 (2.58)
(2.58)
Схема для решения задачи представлена на рисунке 2.3.
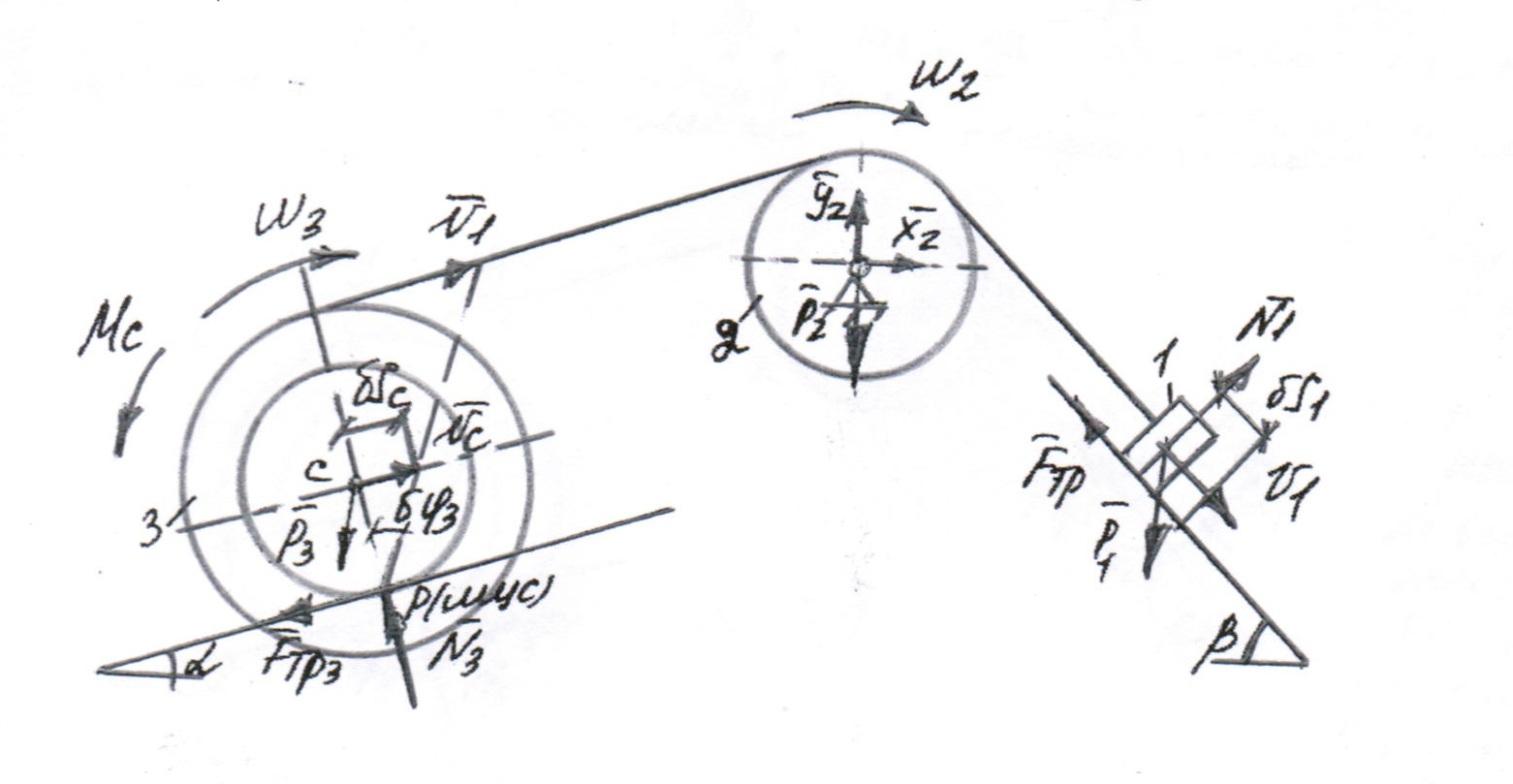
Рисунок 2.3 – Схема для решения задачи по уравнению Лагранжа второго рода
Система имеет одну степень свободы. Запишем уравнение Лагранжа второго рода:
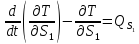 ,(2.59)
,(2.59)
где
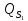 – обобщённая сила.
– обобщённая сила.
Кинетическая энергия системы была найдена в двух предыдущих методах и она равна:
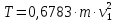 .(2.60)
.(2.60)
Скорость является первой производной от перемещения:
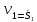 .(2.61)
.(2.61)
Тогда получим выражение вида:
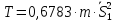 .(2.62)
.(2.62)
Далее вычислим производные:
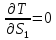 ,(2.63)
,(2.63)
так как координата S не входит в выражение T.
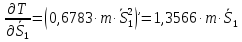 .(2.64)
.(2.64)
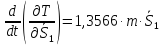 .(2.65)
.(2.65)
Теперь вычислим обобщенную силу. Она представлена выражением:
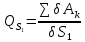 .(2.66)
.(2.66)
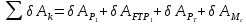 .(2.67)
.(2.67)
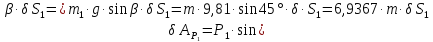 .(2.68)
.(2.68)
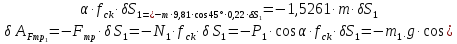 .(2.69)
.(2.69)
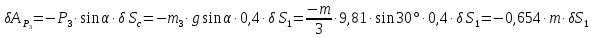 .(2.70)
.(2.70)
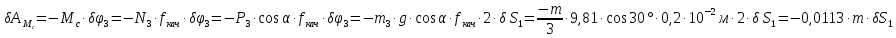 .
(2.70)
.
(2.70)
Подставив значения, рассчитаем обобщённую силу. Получим выражение:
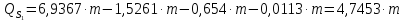 .(2.71)
.(2.71)
Подставив полученные значения в уравнение Лагранжа, найдём ускорение:
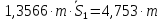 .
(2.72)
.
(2.72)
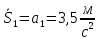 .
.
В завершении найдем скорость. Внешние силы, действующие на механическую систему, постоянные, поэтому движение системы равнопеременное.
Для расчета скорости центра масс тела 1 в тот момент времени , когда он переместится на заданное расстояние S, используем закон равнопеременного движения при начальной скорости, равной нулю
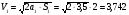 см/c
.
см/c
.
Список использованной литературы
1. Дунаева В.В. Динамика механической системы: Методические указания к выполнению семестрового задания Д-10 по теоретической механике. – Архангельск: Изд-во АГТУ, 2003 – 42с.
2. Морозов С.И., Яковлева Л.П., Ваенский П.Н. Кинематика плоского движения твердого тела: Методические указания к выполнению расчётно-графических заданий по теоритической механике. – Архангельск, ИПЦ САФУ, 2012 – 34с.
