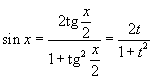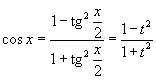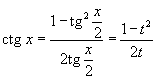шпоры часть 1

 Неопределенный интеграл и его свойства.

Определение первообразной и неопределенного интеграла

Функция F(x) называется первообразной функции f(x), если

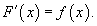
Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) 

и обозначается как

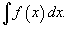
Таким образом, если F - некоторая частная первообразная, то справедливо выражение

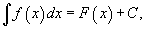
где С - произвольная постоянная. 

Свойства неопределенного интеграла

В приведенных ниже формулах f и g - функции переменной x,

 F - первообразная функции f,  а, k, C - постоянные величины.









   Метод замены переменной

Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением

где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой.  Важно иметь ввиду, что дифференциал dx должен быть заменен на дифференциал новой переменной du.  Для определенного интеграла, кроме этого, необходимо также изменить пределы интегрирования.

Выбираем любое u и находим du= … dx

  Интегрирование по частям

Пусть u(x) и v(x) являются дифференцируемыми функциями. Дифференциал произведения функций u и v определяется формулой

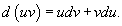
Проинтегрировав обе части этого выражения, получим

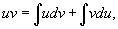
или, переставляя члены,

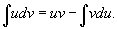
Это и есть формула интегрирования по частям.

 Распределяем u и dv , а потом : du = производная u * dx // v = интеграл от dv  Интегрирование рациональных функций

Для интегрирования рациональной функции 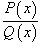, где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:

1. Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;

2. Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;

3. Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;

4. Вычислить интегралы от простейших дробей.

 Интегрирование рациональных выражений тригонометрических функций

Интегрирование любого рационального выражения тригонометрических функций можно всегда свести к интегрированию алгебраической рациональной функции используя универсальную тригонометрическую подстановку x = 2arctg t (или 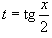).  Для преобразования рациональных выражений от sin x, cos x, tg x, ctg x, sec x и cosec x в алгебраические рациональные функции переменной t применяются следующие тригонометрические формулы:

Чтобы вычислить интеграл вида 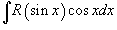, где R - рациональная функция, используется подстановка 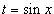.  Аналогично, для вычисления интеграла вида , где R - рациональная функция, используется подстановка 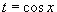.  Если подынтегральное выражение является только функцией tg x, то подстановка t = tg x преобразует такой интеграл в интеграл от рациональной функции. 

Для вычисления интеграла вида 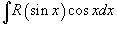, где обе функции sin x и cos x входят в четной степени, применяется подстановка t = tg x и формулы

  Интегрирование некоторых классов тригонометрических функций

1. Интегралы вида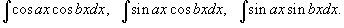 

Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность: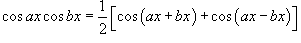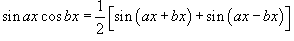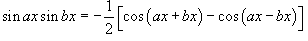

2. Интегралы вида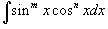 

Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования:

1. Если степень косинуса n - нечетная (при этом степень синуса m может быть любой), то используется подстановка .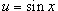

2. Если степень синуса m - нечетная, то используется подстановка .

3. Если степени m и n - четные, то сначала применяются формулы двойного угла

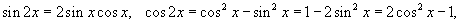
чтобы понизить синуса или косинуса в подынтегральном выражении. Затем, если необходимо, применяются правила a) или b).

3. Интегралы вида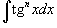 

Степень подынтегрального выражения в данном интеграле можно понизить с помошью тригонометрического соотношения  и формулы редукции

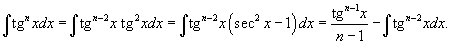
4. Интегралы вида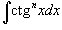 

Здесь степень подынтегрального выражения понижается с помошью соотношения 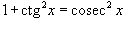 и формулы редукции
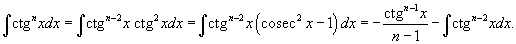