34. Эквивалентная длина

Эквивалентной длиной называют такую длину прямого участка трубопровода данного диаметра, потери напора в котором при пропуске данного расхода равны рассматриваемым местным потерям.

, получаем .

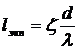Эквивалентной длиной данного местного сопротивления называют такую длину прямого отрезка трубы, которая создает гидравлическое сопротивление, равное сопротивлению детали трубопровода, обусловившей потери напора.

35. Режимы движения жидкости. Основные понятия. Критерий Рейнольдса

1) Ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При таком течении все линии тока жидкости вполне определяются формой русла. При ламинарном течении в трубе все линии тока направлены параллельно оси трубы. Ламинарное течение является упорядоченным при постоянном напоре строго установившегося течения. Ламинарный режим наблюдается преимущественно при движении вязких жидкостей (нефти, смазочных масел и т.п.), и менее вязких жидкостей при их течении с небольшими скоростями.

2) Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсацией скоростей и давления. Движение отдельных частиц оказывается хаотичным, беспорядочным. Наряду с осевым перемещением наблюдается вращательное и поперечное перемещение отдельных объемов жидкости. Этим и объясняются пульсации скоростей и давления.

- Безразмерный комплекс величин , значение которого позволяет судить о режиме движения жидкости, называется критерием Рейнольдса (Re)

При режим движения жидкости будет ламинарным. При Re>3000 режим турбулентный. При 2300 ≤ Re ≤ 3000 переходный режим.

Если жидкость движется по трубе круглого сечения, то в формулу (чуть выше) подставляют внутренний диаметр трубы . Если жидкость движется по каналу некруглого сечения, то подставляют, так называемый, эквивалентный диаметр , равный отношению учетверённой площади сечения потока к смоченному периметру канала: d_э= 4F / П.

36. Основное уравнение равномерного движения

Рассмотрим прямолинейное равномерное движение жидкости. Живые сечения в этом случае могут быть произвольной формы, но не должны изменяться по всей длине рассматриваемого участка. В таком потоке потери напора определяются лишь потерями по длине.

Выделим из потока участок жидкости длиной l и запишем уравнение Бернулли для сечений 1 и 2( рис. 32 )

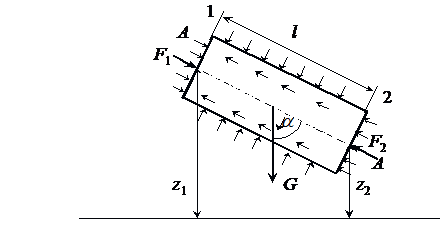
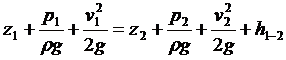
где z1 , z2 - ординаты центра тяжести сечений 1,2; p1 , p2 - давление в центрах тяжести этих сечений,

v1 , v2 - средние скорости в этих сечениях, h1-2 - потери напора по длине.

Так как движение равномерное, то v1 =v2 и уравнение можно переписать так: .

Для вычисления этой разности напишем сумму проекций на ось А-А всех сил, действующих на участке 1-2. Эти силы следующие:

1) сила тяжести жидкости

2) силы давления на плоские сечения , , ,

3) сила трения ,

где t - сила трения на единицу площади смачиваемой поверхности русла, c - смоченный периметр,

4) силы давления стенок на жидкость ( эти силы не подсчитываем, так как они параллельны оси А-Аи, следовательно, их проекции на ось А-А равны нулю ). Спроектируем все эти силы на ось А-А: Из рисунка .

Подставим выражение для сил в уравнение .

Разделим обе части этого равенства на , имеем

Сравнивая выражения, находим , откуда . Отношение площади живого сечения S к смоченному периметру c называется гидравлическим радиусом

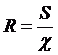. Величина обозначается через i и называется гидравлическим уклоном. Получаем - Это уравнение называется основным уравнением равномерного движения.