
- •1. Определение гидравлики. Основные понятия и определения. Сплошная среда.
- •2. Основные физические свойства жидкостей.
- •3. Силы, действующие в жидкости. Гидростатическое давление - определение.
- •4. Давление абсолютное, избыточное и вакуумметрическое.
- •5. Свойства гидростатического давления.
- •6. Эпюры гидростатического давления.
- •7. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера).
- •8. Основное дифференциальное уравнение гидростатики.
- •9. Основное уравнение гидростатики (закон Паскаля).
- •10 Геометрическое и энергетическое понятия основного уравнения гидростатики.
- •11. Поверхности равного давления
- •12. Относительный покой жидкости
- •3.1.2 Относительный покой при вращении вокруг вертикальной оси
- •13. Сила давления жидкости на плоскую стенку
- •14.Приборы дл измерения давления
- •15. Гидростатический парадокс
- •16. Сила давления на криволинейную поверхность. Тело давления
- •17. Закон Архимеда
- •18. Равновесие тела в покоящейся жидкости
- •19.Определение толщины стенок цилиндрических труб
- •20.Идеальная и реальная жидкости. Закон Ньютона о внутреннем трении
- •22. Гидравлические элементы потока
- •23. Методы определения движения жидкости (метод Лагранжа и метод Эйлера).
- •24 Уравнение неразрывности (уравнение сохранения массы)
- •25. Расход жидкости (массовый, объемный, весовой).
- •26. Уравнение Бернулли для струйки идеальной жидкости. Геометрический и физический смысл уравнения Бернулли.
- •27. Гидравлический и пьезометрический уклоны.
- •28 Графическое представление уравнения Бернулли для струйки идеальной и реальной жидкости.
- •30. Графическое представление уравнения Бернулли для потока идеальной и реальной жидкости.
- •31. Примеры использования уравнения Бернулли (трубка Пито, Пито-Прандтля, расходомеры и т.Д.)
- •3) Расходомер Вентури.
- •4) Формула Торричелли
- •6) Водоструйный насос
- •7)Ракета
- •32. Классификация гидравлических потерь
- •33.Структура потока в области местных сопротивлений
- •34. Эквивалентная длина
- •35. Режимы движения жидкости. Основные понятия. Критерий Рейнольдса
- •36. Основное уравнение равномерного движения
- •37. Эпюры скоростей при ламинарном и турбулентном режимах движения жидкости
- •38. Определение эквивалентной шероховатости. Гидравлически гладкие и шероховатые поверхности
- •39.Метод наложения потерь. Коэффициент сопротивления системы
- •Коэффициент сопротивления системы
- •40. Кавитация.
- •41 Определение гидравлического удара. Прямой и непрямой гидравлический удар. Скорость распространения ударной волны.
- •42.Назначение и классификация трубопроводов.
- •43.Гидравлические характеристики трубопровода (график зависимости потерь напора в трубопроводе от пропускаемого расхода).
- •44.Определение экономически выгодного диаметра трубопровода (график).
26. Уравнение Бернулли для струйки идеальной жидкости. Геометрический и физический смысл уравнения Бернулли.
Рассмотрим элементарную струйку реальной жидкости также при установившемся движении.
При движении элементарной струйки реальной жидкости общий запас удельной механической энергии не может оставаться постоянным, как это рассматривалось при движении идеальной жидкости. Дело в том, что при движении реальной жидкости вследствие ее вязкости возникают сопротивления движению, на преодоление которых затрачивается часть механической энергии.
При продвижении от одного сечения к другому удельная энергия в струйке (а значит, и напор) будет уменьшаться. Энергия в первом (вышерасположенном по течению) сечении при движении вязкой жидкости всегда больше, чем во втором (нижерасположенном) сечении, на значение потерь удельной энергии между этими сечениями. Потери удельной энергии можно выразить через потери напора hтр. Как и все остальные члены уравнения (1.55), hтр имеет линейную размерность. Окончательно уравнение Бернулли для струйки реальной жидкости имеет вид:
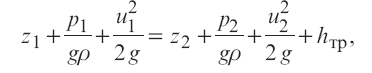 (1.56)
(1.56)
т.е. отличается от (1.54) наличием потерь напора. В этом случае напорная линия (линия удельной энергии) будет снижаться по направлению движения.
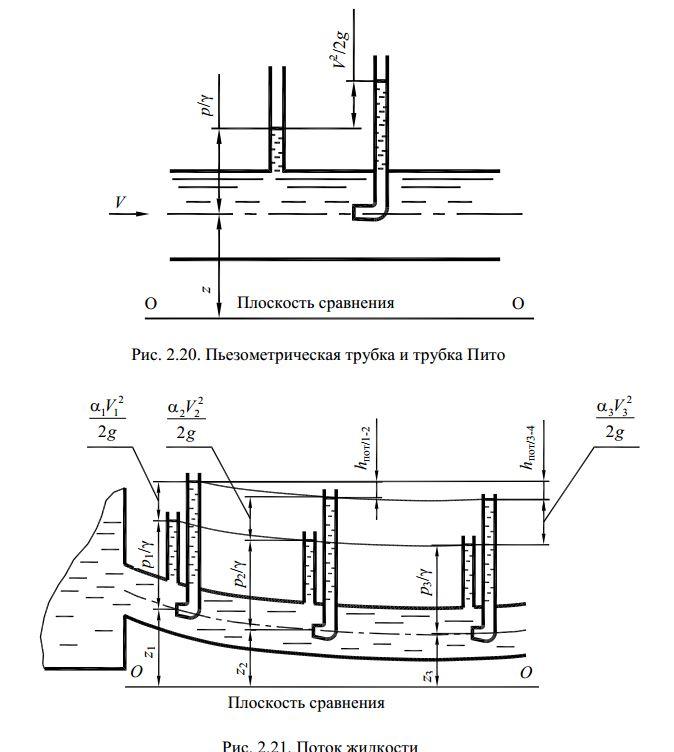
Геометрическая интерпретация уравнения Бернулли Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.
Как и в гидростатике, величину Zназываютнивелирной высотой.
Второе слагаемое -
 носит названиепьезометрическая
высота. Эта величина соответствует
высоте, на которую поднимется жидкость
в пьезометре, если его установить в
рассматриваемом сечении, под действием
давленияP.
носит названиепьезометрическая
высота. Эта величина соответствует
высоте, на которую поднимется жидкость
в пьезометре, если его установить в
рассматриваемом сечении, под действием
давленияP.Сумма первых двух членов уравнения
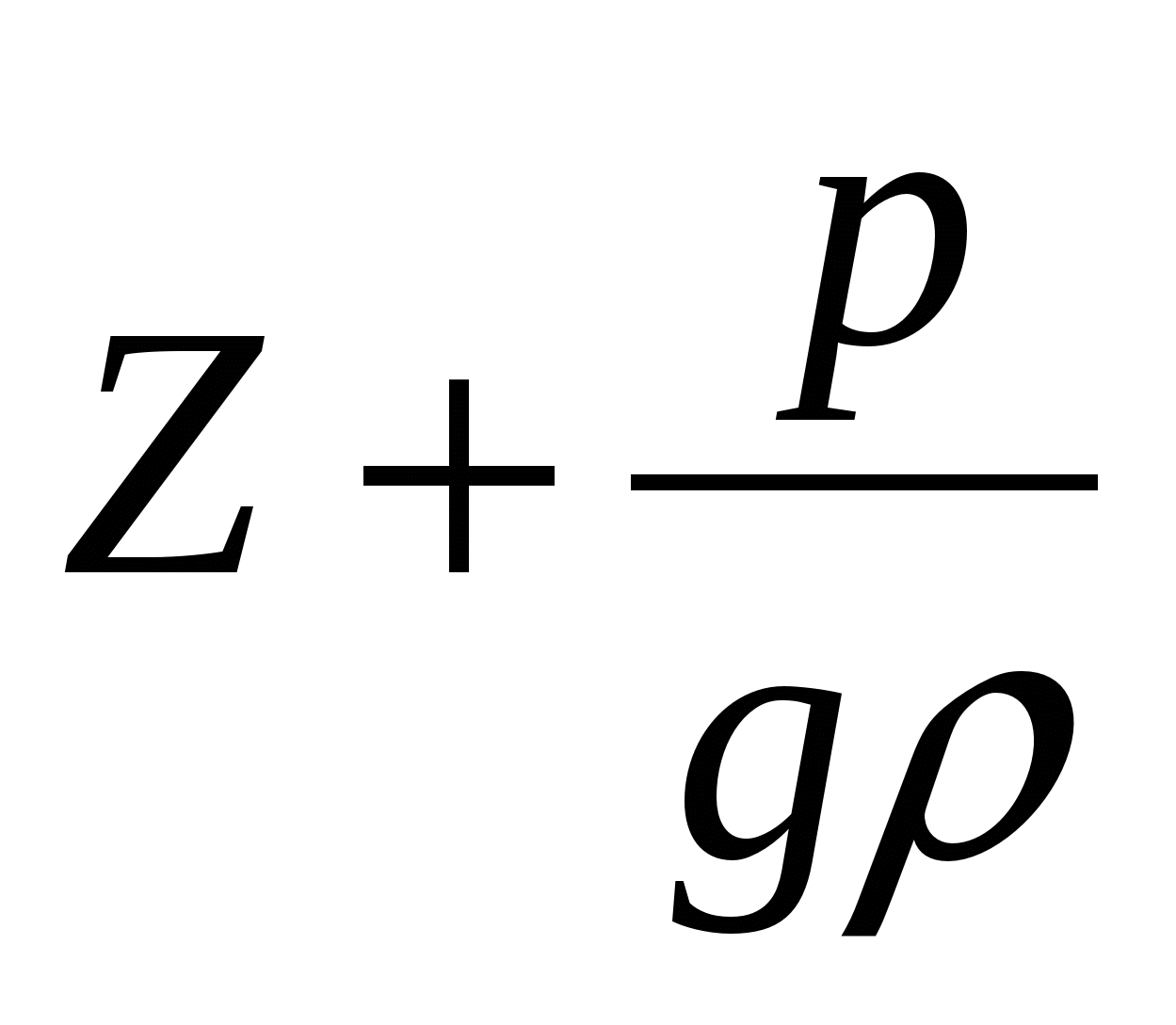 гидростатический
напор.
гидростатический
напор.Третье слагаемое в уравнения Бернулли
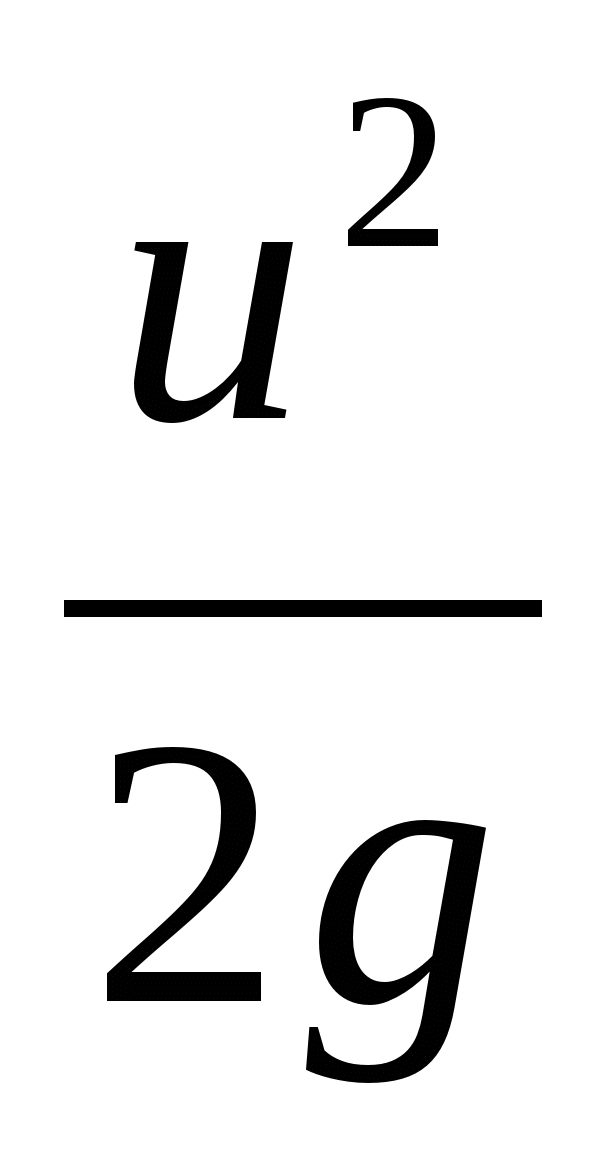 называетсяскоростной высотойилискоростным напором. Данную
величину можно представить как высоту,
на которую поднимется жидкость, начавшая
двигаться вертикально со скоростьuпри отсутствии сопротивления движению.
называетсяскоростной высотойилискоростным напором. Данную
величину можно представить как высоту,
на которую поднимется жидкость, начавшая
двигаться вертикально со скоростьuпри отсутствии сопротивления движению.Сумму всех трёх членов (высот) называют гидродинамическим или полным напороми, как уже было сказано, обозначают буквойН.
Физический смысл уравнения Бернулли
Согласно уравнению Бернулли сумма трех указанных величин является постоянной, что приводит к равенству: de1= de2.
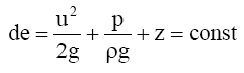
Итак, сумма трех членов уравнения Бернулли есть сумма трех удельных энергий: удельной кинетической энергии, удельной потенциальной энергии давления и удельной потенциальной энергии положения. Для идеальной жидкости сумма трех удельных энергий по длине элементарной струйки – постоянна.
В общем, уравнение Бернулли является специальным выражением основного физического закона сохранения энергии
27. Гидравлический и пьезометрический уклоны.
ГИДРАВЛИЧЕСКИЙ УКЛОН (гидравлический градиент) - потери уд. энергии (напора)жидкости на единицу длины потока:
![]() где
dh
- потеря напора
на длине ds,
выражение в скобках (трёхчлен Бернулли,
см. Бернулли
уравнение)
- уд. энергия
потока. В частном случае движения в
трубах с пост. диаметром (равномерное
движение), когда кинетич. энергия по
длине потока не изменяется, Г. у. совпадает
спьезометрическим
уклоном, а
при равномерном движении в каналах - с
уклоном дна канала.
где
dh
- потеря напора
на длине ds,
выражение в скобках (трёхчлен Бернулли,
см. Бернулли
уравнение)
- уд. энергия
потока. В частном случае движения в
трубах с пост. диаметром (равномерное
движение), когда кинетич. энергия по
длине потока не изменяется, Г. у. совпадает
спьезометрическим
уклоном, а
при равномерном движении в каналах - с
уклоном дна канала.
Пьезометрическим уклоном называют изменение удельной потенциальной энергии жидкости вдоль потока, приходящееся на единицу его длины.
Если гидравлический уклон всегда положителен, то пьезометрический может быть и положительным, и отрицательным. При равномерном движении жидкости, когда скорость по длине потока не изменяется, скоростной напор вдоль потока av2/ (2g) = const. Следовательно, пьезометрическая линия параллельна энергетической, и пьезометрический уклон равен гидравлическому.
Изменение удельной потенциальной энергии положения вдоль потока жидкости, приходящееся на единицу длины, называют геометрическим уклоном i и определяют по формуле
![]()
 где
l
— расстояние
между сечениями потока.
где
l
— расстояние
между сечениями потока.
