Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования

«Ярославская государственная сельскохозяйственная академия»

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Ярославль

2013

УДК 515/518

Корякина А.П., Передбогов А.П., Шегелев Ю.П. Начертательная геометрия: Конспект лекций / РАТИ – Рыбинск, 1993 – 119 с.

Настоящий конспект содержит лекции, включаемые в учебную дисциплину «Начертательная геометрия. Инженерная графика». Предназначен для студентов технических вузов и слушателей ФПК ИТР промышленных предприятий, а также может быть использован студентами не машиностроительных специальностей при изучении курса «Начертательная геометрия».

Конспект лекций содержит десять разделов, в которых раскрываются основы начертательной геометрии. Некоторые разделы содержат также элементы вычислительной геометрии, которые дают возможность рассматривать математические модели объектов, изучаемых в курсе, и применять их при составлении алгоритмов для решения задач на ЭВМ.

Лекционный курс подготовлен на кафедре «Начертательная геометрия и графика» Рыбинского авиационного технологического института.

Рецензенты: кафедра начертательной геометрии и графики

Ярославского политехнического института;

Кандидат технических наук Кирсанов В.Н.

ISBN 5-230-14262-6 Рыбинский авиационный

Технологический институт,

1993

Оглавление

Предмет начертательной геометрии…………………………………………………………………..2

1. Метод проецирования………………………………………………………………………….3

   1. Центральное проецирование………………………………………………………………3

   2. Параллельное проецирование……………………………………………………………..3

   3. Способы дополнения проекционного чертежа…………………………………………..5

   4. Порядок построения комплексного чертежа…………………………………………….6

   5. Проекции прямоугольных осей координат на комплексном чертеже…………………7

   6. Метод замены плоскостей проекций……………………………………………………...8

2. Комплексный чертеж прямой и плоскости и их аналитические модели………………….9

   1. Комплексный чертеж прямой……………………………………………………………..9

   2. Аналитическая модель прямой…………………………………………………………..11

   3. Взаимное расположение линейных геометрических элементов……………………...11

   4. Комплексный чертеж плоскости………………………………………………………...13

   5. Взаимное положение точки, прямой и плоскости……………………………………..15

   6. Кривые линии и их проекции…………………………………………………………….17

   7. Линии второго порядка…………………………………………………………………...18

   8. Пространственные кривые……………………………………………………………….21

3. Поверхности…………………………………………………………………………………...21

   1. Образование, задание и изображение поверхностей…………………………………..21

   2. Поверхности плоско – параллельного перемещения…………………………………..23

   3. Поверхности вращения…………………………………………………………………...23

   4. Уравнение поверхности вращения………………………………………………………24

   5. Линейчатые поверхности………………………………………………………………...27

   6. Уравнение линейчатой поверхности……………………………………………………30

   7. Поверхности второго порядка…………………………………………………………...31

   8. Циклические поверхности………………………………………………………………..33

   9. Пример составления уравнения циклической поверхности…………………………..33

   10. Графические поверхности……………………………………………………………33

4. Взаимное положение поверхностей…………………………………………………………34

   1. Метод вспомогательных секущих плоскостей…………………………………………35

   2. Метод вспомогательных секущих сфер…………………………………………………37

   3. Особые случаи пересечения поверхностей второго порядка………………………….39

5. Метод вращения………………………………………………………………………………41

6. Пересечение линии и поверхности…………………………………………………………..42

7. Математическая модель линии пересечения поверхностей второго порядка……………45

8. Метрические задачи…………………………………………………………………………..47

   1. Условия перпендикулярности на комплексном чертеже………………………………47

   2. Способы решения некоторых метрических задач……………………………………...50

   3. Нормаль поверхности…………………………………………………………………….55

9. Развертки поверхностей……………………………………………………………………...57

   1. Построение разверток многогранных поверхностей…………………………………..57

   2. Построение приближенных разверток развертывающихся поверхностей…………..60

   3. Построение условных разверток неразвертывающихся поверхностей………………63

10. Аксонометрические поверхности…………………………………………………………...67

    1. Коэффициенты искажения……………………………………………………………67

    2. Основная теорема аксонометрии…………………………………………………….67

    3. Основные виды аксонометрических поверхностей………………………………..67

Предмет начертательной геометрии

В инженерной практике, исследовательской работе, в процессе передачи информации и во множестве других случаев человек использует различные модели. Модель никогда не повторяет объект или явление полностью и несет о них только основную информацию. Например: чертеж механизма передает информацию о размерах, форме, взаимодействии составных частей и т.д.; конспект лекций передает только содержание лекции, при этом не воспроизводя голос преподавателя, его жестикуляцию и т.д.; рисунок несет информацию о форме и цвете изображенного объекта и т.д.

Посредствам моделей информацию не только передают, но и перерабатывают: математик преобразовывает формулы, конструктор с помощью чертежа может усовершенствовать механизм, композитор пользуясь нотной записью, обрабатывает музыку. Таких примеров можно приводить очень много.

В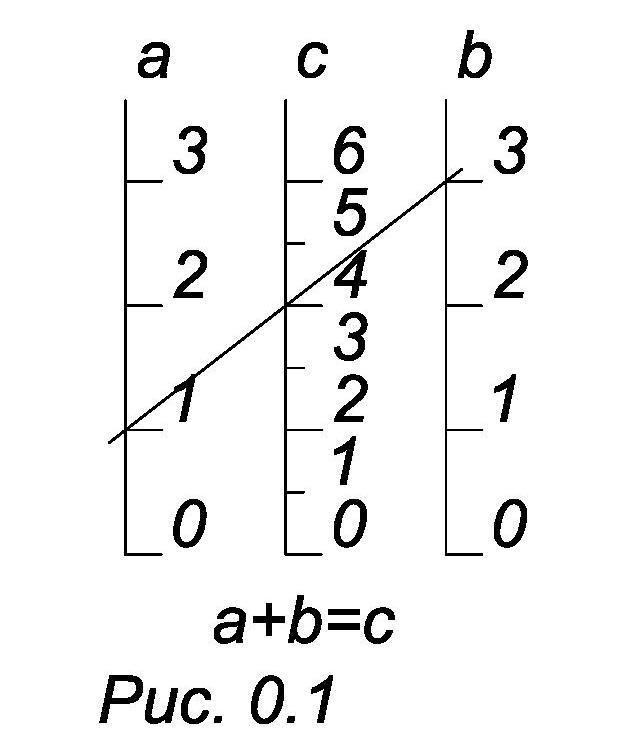наше время особое место занимают математические модели, которые делятся на два класса: аналитические и геометрические. К геометрическим моделям относятся: чертеж, рисунок, фотоснимок, рентгенограмма, номограмма и др. Номограмма это чертеж, который служит для облегчения и ускорения математических вычислений при технических расчетах. Наряду с понятием «номограмма» используется более точный термин – расчетно – геометрическая модель. Логарифмическая линейка, например, позволяет быстро производить умножение, деление и другие арифметические действия. Одной из простейших номограмм из выровненных точек является номограмма сложения. Работает она следующим образом: прикладываем линейку к точкам, соответствующим данным значениям, на шкалах а иb (рис. 0.1). На шкале С в точке пересечения шкалы линейки читаем ответ.

Расчетно – геометрические модели имеют широкое применение в инженерной практике. Конструировать их можно аналитически и геометрически.

Начертательная геометрия изучает модель для передачи и переработки геометрической информации.

Модели бывают однозначные (изоморфные) многозначные (гомоморфные). Примером однозначной модели студенческой группы является список фамилий, если в группе нет однофамильцев. Список группы чаще всего модель многозначная, так как одно и тоже имя может принадлежать нескольким студентам. Гомоморфные модели тоже несут информацию (иногда очень существенную) о изучаемом объекте.

Знакомство с начертательной геометрией начинают с построения гомоморфных геометрических моделей, после чего рассматривают способы позволяющие переходить к кэоморфным моделям.

Основным методом начертательной геометрии является способ проецирования. Определить проецирование, значит указать алгоритм, посредствам которого точки одного пространства сопоставляются точками другого пространства. Условимся обозначать одномерное пространство (линия) R¹, двумерное пространство (поверхность) R², трехмерное пространство R³, …….., n-мерное пространство Rⁿ. В дальнейшем будем рассматривать проецирование трехмерных геометрических образов не плоскость.

1. Метод проецирования

1. Центральное проецирование

Посредством центрального проецирования осуществляется моделирование трехмерных геометрических образов на плоскость. Аппарат проецирования: плоскость проекции и центр проецирования (рис. 1.1)

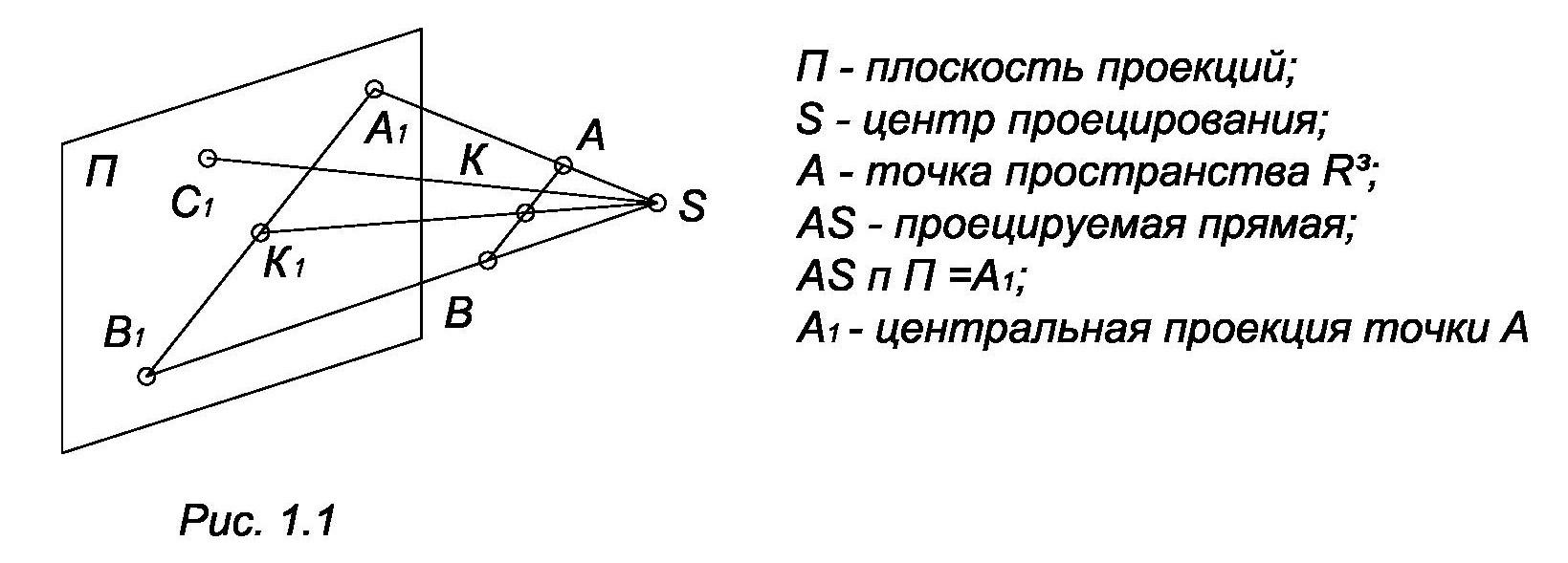
Проецирование рассмотренное на рис. 1.1 называется линейным, так как проецирующие образы – прямые (плоскости). В качестве проецирующих линий в некоторых случаях выбирают кривые линии. В этом случае проецирование называется нелинейным.

Предположим, что требуется спроецировать центральную прямую АВ. Нетрудно отметить, что все проецирующие прямые принадлежат плоскости SАВ (проецирующая плоскость). Эта плоскость пересекает плоскость проекции П по прямой А₁В₁. Следовательно, проекцией прямой линии в общем случае является прямая линия. В частном случае, прямая проецируется в точку, если она проходит через центр проецирования.

Заметим, что построенная таким образом на плоскости П модель пространства является гомоморфной (многозначной). Действительно, попытаемся по данной проекции С₁ определить точку С в пространстве. Оказывается таких точек бесконечное множество, это все точки прямой S₁C₁. Но и эта модель несет некоторую информацию. Например, проекция точки определяет проецирующую прямую, которой принадлежит данная точка.

2. Параллельное проецирование

Если центр проецирования бесконечно удаленная точка, то проецирующие прямые параллельны между собой и проецирование называется параллельным. Чтобы задать параллельное проецирование, необходимо задать плоскость проецирования П и направление проецирования s. Направление проецирования не должно быть параллельно плоскости проекции (рис. 1.2) Если s перпендикулярно П, то проецирование называется ортогональным (рис. 1.3).

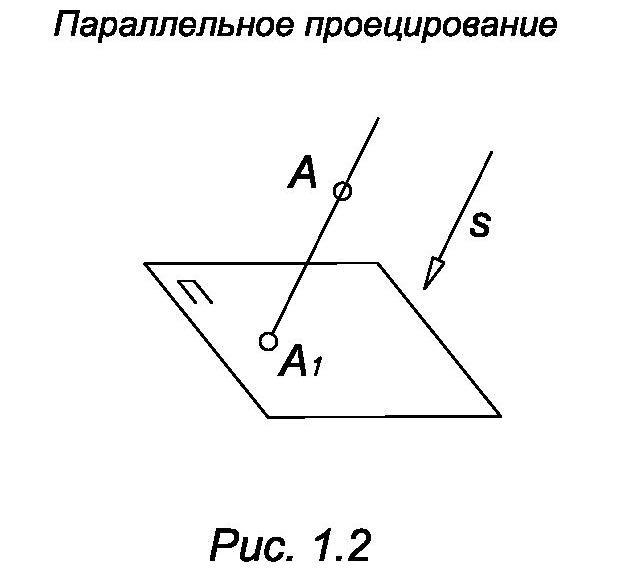
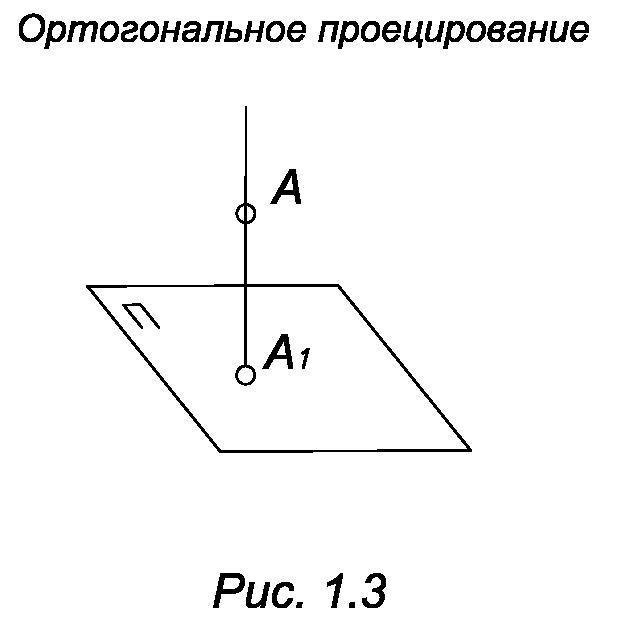
Таблица 1.1 Основные свойства проецирования

Центральное проецирование	Параллельное проецирование	Ортогональное проецирование
Проекцией точки является точка. Проекцией прямой линии является прямая линия. Проекцией точки, принадлежащей некоторой прямой, является точка принадлежащая проекции данной прямой.
	Если прямые параллельны, то при параллельном проецировании их проекции параллельны или совпадают, или обе прямые проецируются в точки. Отношение проекций отрезков, принадлежащих параллельным прямым или одной и той же прямой, равно отношению самих отрезков. Проекция фигуры не меняется при параллельном переносе плоскости проекций.
		/А1В1/ = /АВ/ cosa, где а – угол наклона АВ к плоскости проекций.

П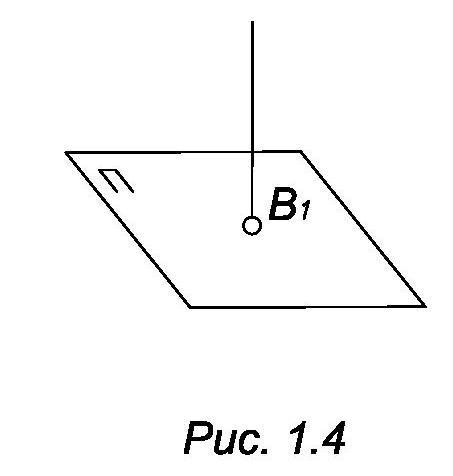ри проецировании трехмерных объектов на плоскость, т.е. при переходе отR³ к R², получается гомоморфная модель объекта. Значит, рассматриваемые нами методы проецирования позволяют однозначно решить прямую задачу: по данному трехмерному объекту строить его проекцию на плоскость. Однако, обратная задача – по данной проекции воспроизвести (реконструировать) оригинал – однозначно не решается. Эта задача допускает бесконечное множество решений, т.к. каждую точку В₁ плоскости П (рис. 1.4) можно считать проекцией любой точки проецирующей прямой, проходящей через В_1. Чтобы добиться однозначности, следует дополнить проекционный чертеж, сделать его «обратимым», т.е. чертежом вполне определяющим данный геометрический объект. Существует много способов в дополнения проекционного чертежа. Остановимся на некоторых из них.

3. Способы дополнения проекционного чертежа

П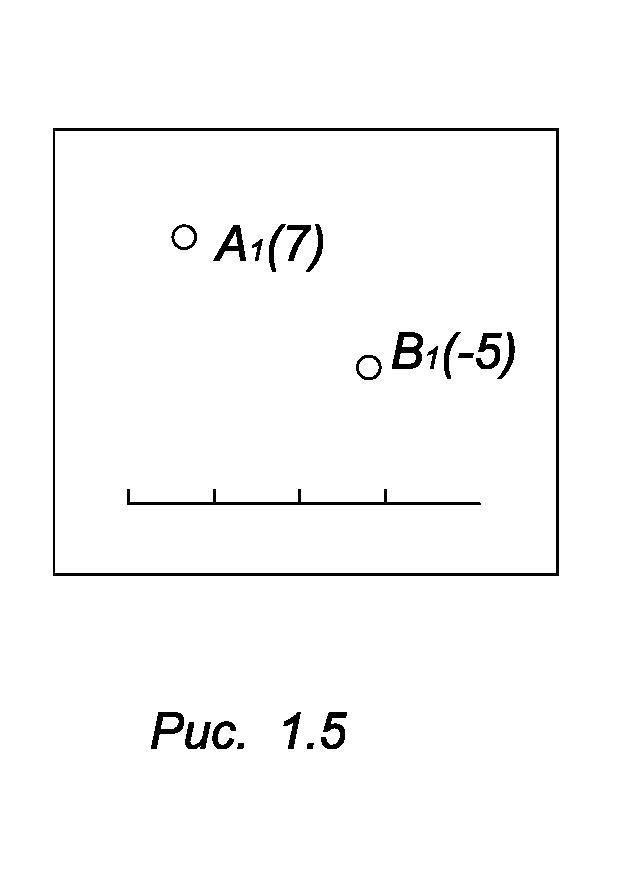роекции с числовыми (высотными) отметками (рис. 1.5). Число, стоящее в скобках рядом с обозначением проекции точки, задает расстояние от данной точки до плоскости проекций. Если число положительное, значит точка находится перед плоскостью проекций, если отрицательное, то точка за плоскостью проекций.

Векторные чертежи (способ Е.С. Федорова) (рис. 1.6.). Расстояние от точки до плоскости проекций задается посредством отрезков на плоскости проекций, начало отрезка совпадает с проекцией данной точки. Такие отрезки называются высотными. Они параллельны между собой. По направлению отрезка можно судить о том, где находится данная точка, перед плоскостью или за ней. Например, точка А – перед плоскостью проекций, В – за плоскостью проекций.

Аксонометрические проекции (рис. 1.7). Для получения аксонометрической проекции необходимо выполнить следующие действия:

1. Связать изображаемый объект с прямоугольной декартовой системой координат. Тогда для каждой точки можно построить координатную ломаную линию.

2. Спроецировать параллельно объект вместе с координатными осями на плоскость проекций, которая называется аксонометрической. Проекции осей координат называются аксонометрическими осями. Проекции масштабных отрезков называются аксонометрическими масштабами. Проекции координатной ломанной линии называется аксонометрической координатной ломаной.

X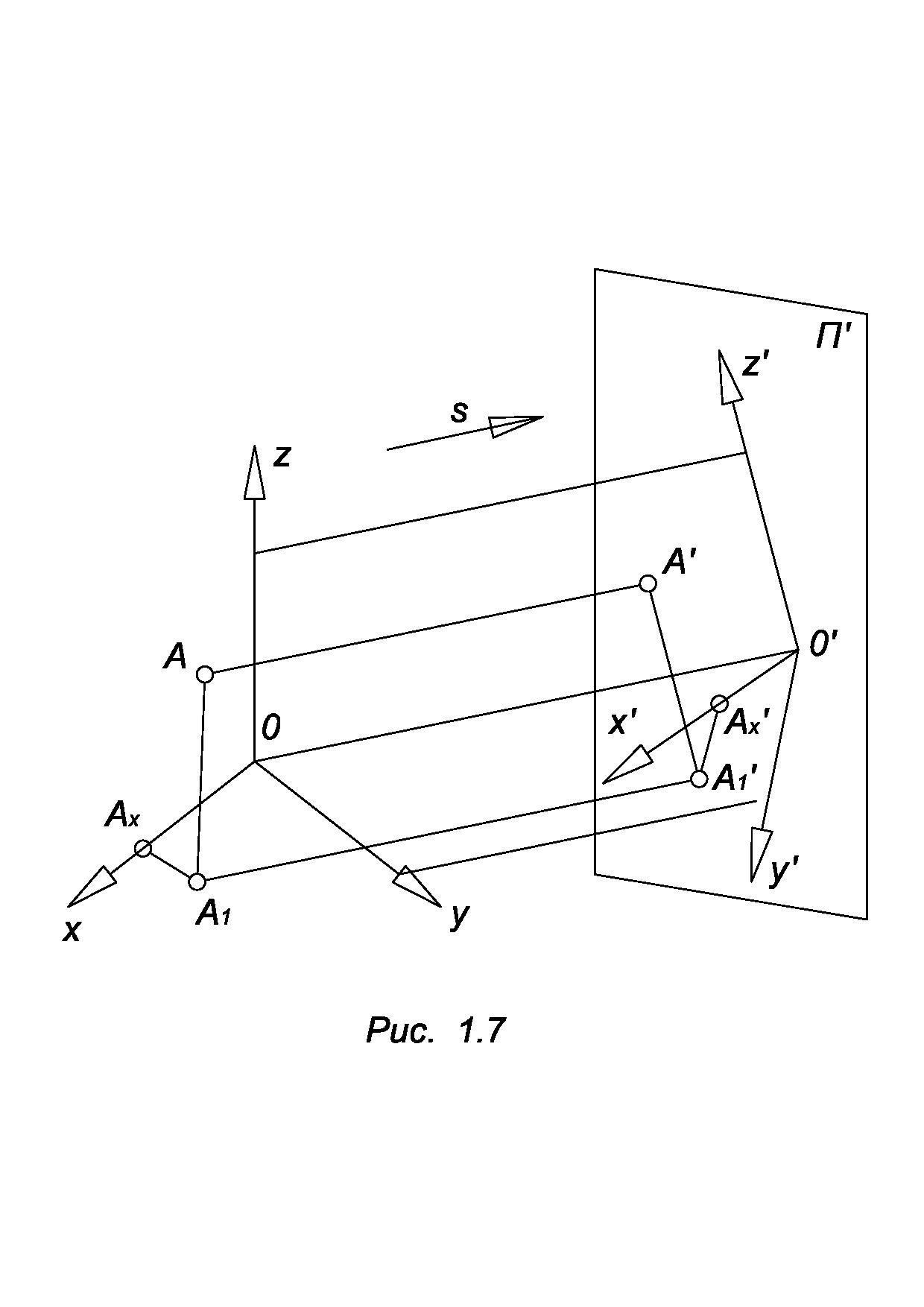^’, Y^’, Z^’ – аксонометрические оси.

О^’А^’_x А^’₁ А^’ – аксонометрическая координатная ломаная линия.

А^’ – аксонометрическая проекция точки А.

А^’₁ – вторичная проекция точки А, или аксонометрическое изображение проекции данной точки на плоскость xОy.

Однозначность аксонометрической проекции достигается с помощью задания аксонометрической ломанной линии или вторичной проекции изображенного объекта.

Комплексный чертеж

Этот способ получил наибольшее применение в технической практике. Однозначность модели достигается посредством использования двух связанных проекций геометрического объекта. Существует много способов образования комплексного чертежа. Познакомимся с одним из них.

4. Порядок построения комплексного чертежа.

Для построения комплексного чертежа необходимо выполнить следующие действия:

1. Выбрать две взаимно перпендикулярные плоскости П₁ и П₂ (рис. 1.8).

П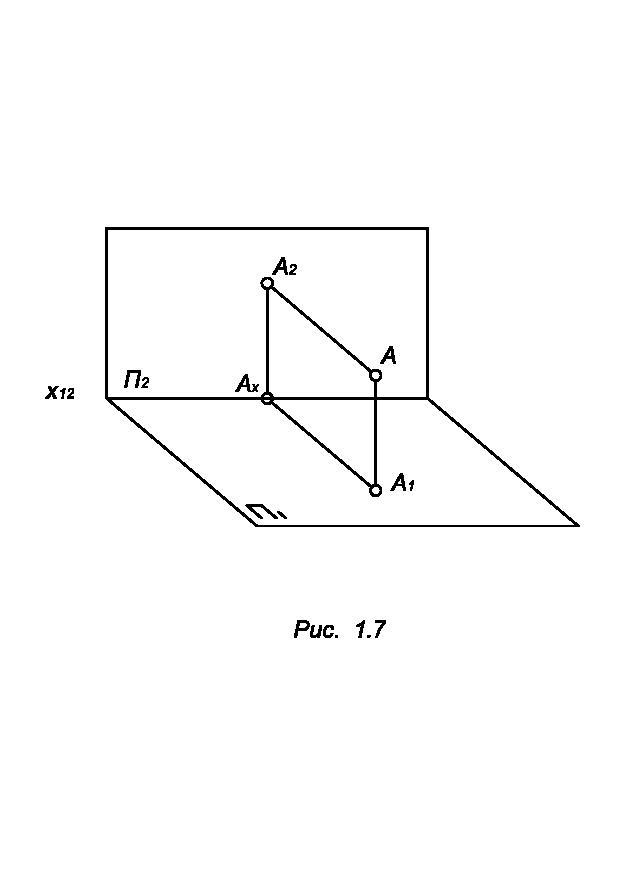₁ – горизонтальная плоскость проекций;

П₂ – фронтальная плоскость проекций;

П₁П П₂ = X₁₂, где X₁₂ – ось проекций.

2. Геометрический объект, например точка А, проецируется ортогонально на каждую плоскостей проекций.

А₁ – горизонтальная проекция точки А;

А₂ – фронтальная проекция точки А;

АА_{1 ┴} П₁, следовательно, А₂А_{x ┴} X₁₂,

А А_{2 ┴} П₂, следовательно, , А₁А_{x ┴} X₁₂,

/ А₂ А_x/ = /АА₁/ - высота точки, / А₁ А_x/ = /АА₂/ - глубина точки.

3. Плоскости проекций совмещают с плоскостью чертежа (рис. 1.9).

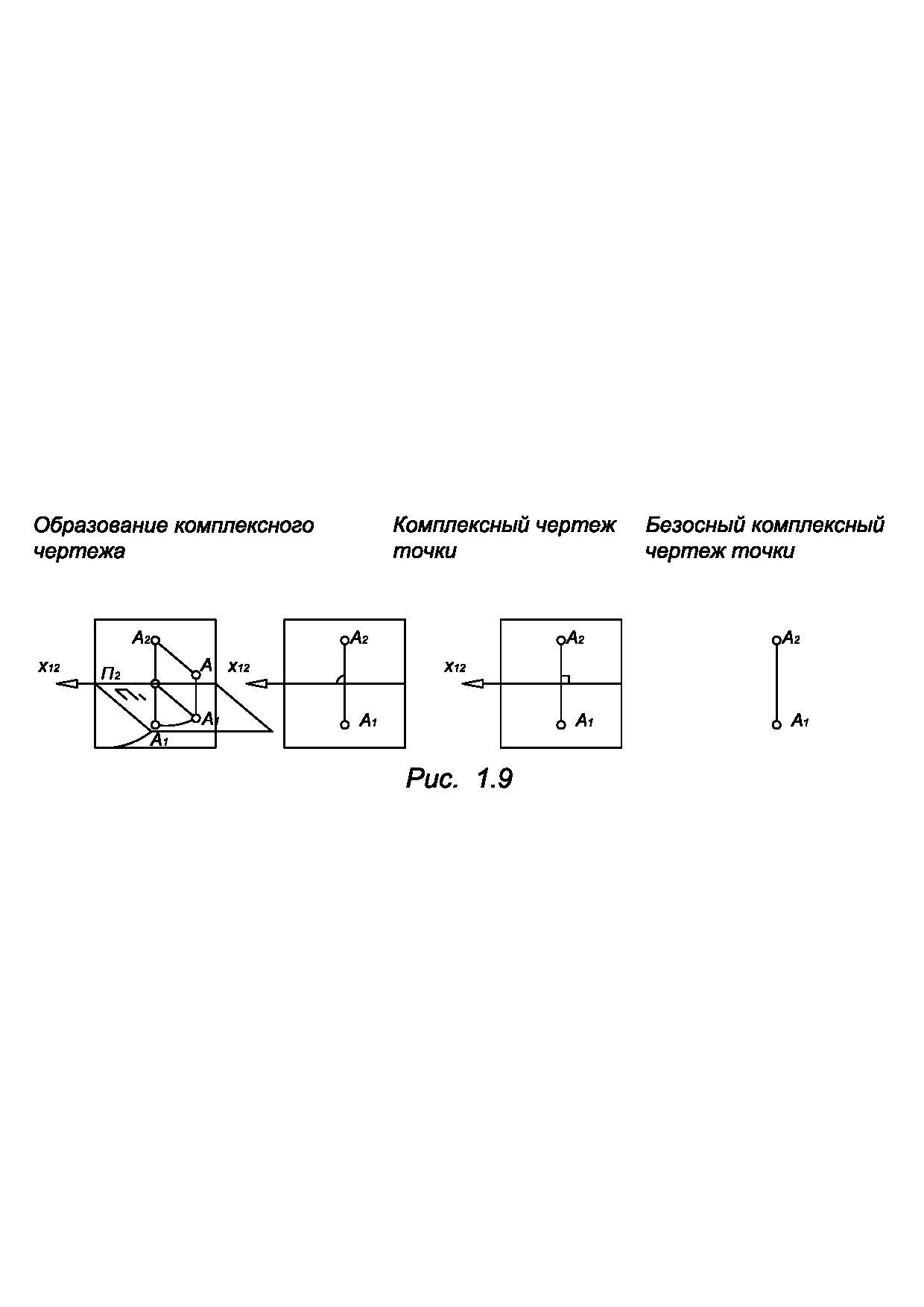
Полученный чертеж является обратным. Действительно, если фронтальной проекции А₁ поставить перпендикуляр к плоскости чертежа и от точки А₂ отложить на этом перпендикуляре, отрезок равный глубине точки, то однозначно определиться положение точки А. Т.о. изоморфной моделью точки пространства R³ является пара связанных точек плоскости.

5. Проекции прямоугольных осей координат на комплексном чертеже

В начертательной геометрии чаще пользуются правой прямоугольной системой координат (рис. 1.10). Относительно плоскостей проекций оси координат целесообразно располагать следующим образом: О_x║П_1, О_z║П₂, О_x║П₂ и О_y║П₁ (рис. 1/11). В частном случае, если нет необходимости на чертеже рассматривать точки с отрицательным значением координат y и z, проекции О₁X₁ и О₂X₂ могут совпадать.

На рис. 1.12 дан комплексный чертеж точек А (-3, 4, -1); В (4, -2, 3); С (6, -1, -1).

В предыдущих примерах в качестве геометрического объекта рассматривались отдельные точки. Заметим, что для одной точки выбор плоскостей проекций не имеет значения, но для решения задач, в условия которых включены прямые, плоскости и др. объекты, выбор той или другой плоскости проекций может упростить или усложнить решение задачи. Например, в некоторых случаях задача упрощается, если плоскость проекций выбирать параллельно, или перпендикулярно данным геометрическим объектам. Переход от данной системы плоскостей проекций к новой можно осуществлять с помощью методов преобразования комплексного чертежа, самым распространенным на которых является метод замены плоскостей проекций.

6. Метод замены плоскостей проекций

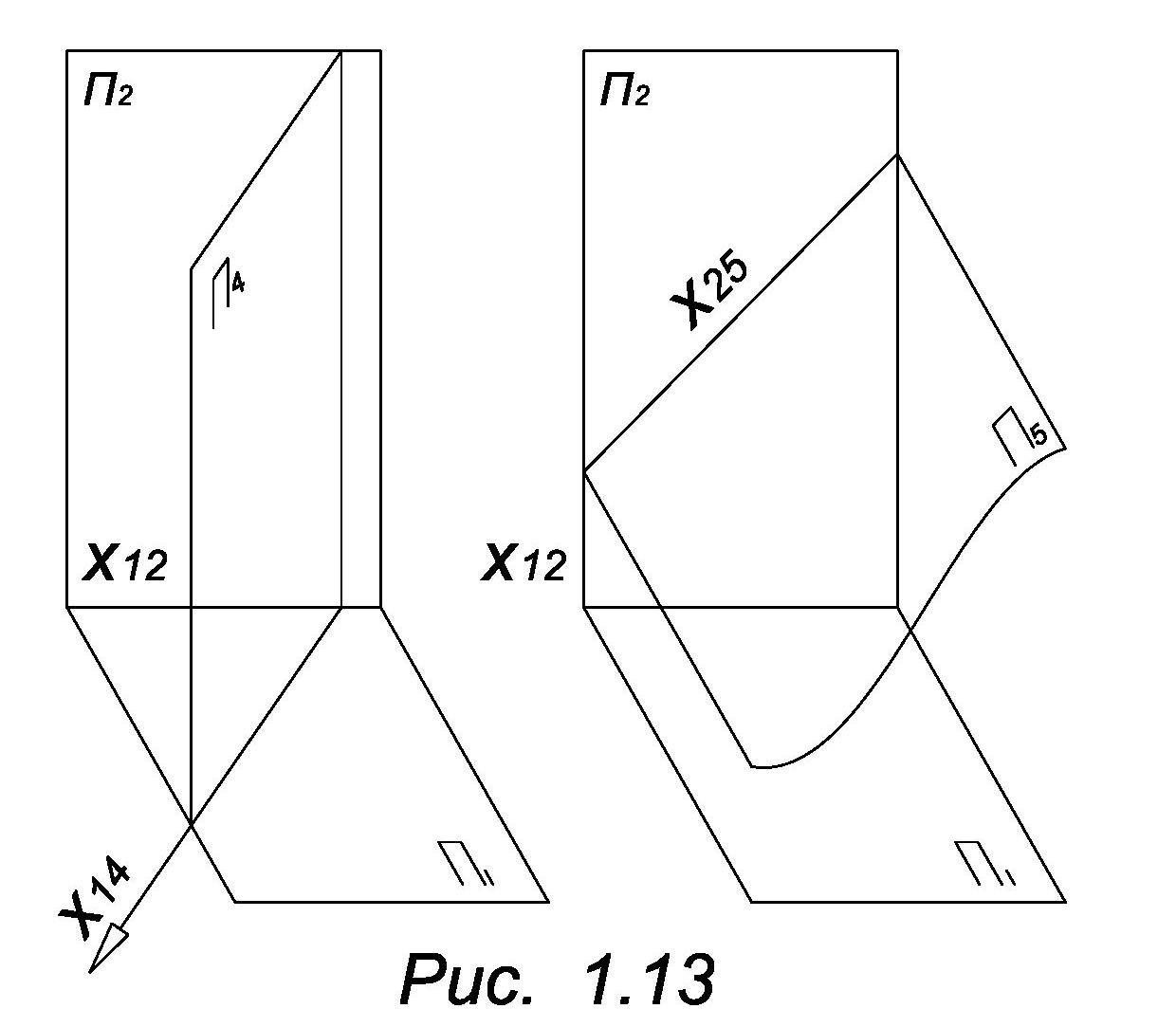Метод замены плоскостей проекций состоит в переходе от данной системы плоскостей (старая система) к новой системе взаимно перпендикулярных плоскостей проекций. Положение самого объекта в пространстве остается неизменным.

Иногда для решения задач достаточно заменить только одну из данных плоскостей проекций, например, плоскость П₂ на плоскость П₄, П_{4 ┴} П₁. Или плоскость П₁ на плоскость П₅, П_{5 ┴} П₂, (рис. 1.13). Этот метод применяется так же для построения дополнительной проекции, если необходимо на чертеже полнее изобразить геометрический объект.

Рассмотрим подробнее метод на примере построения дополнительной проекции точки (рис. 1.14 и рис. 1.15). Заметим, что применяя метод замены плоскостей проекций, следует фиксировать ось проекций на комплексном чертеже.

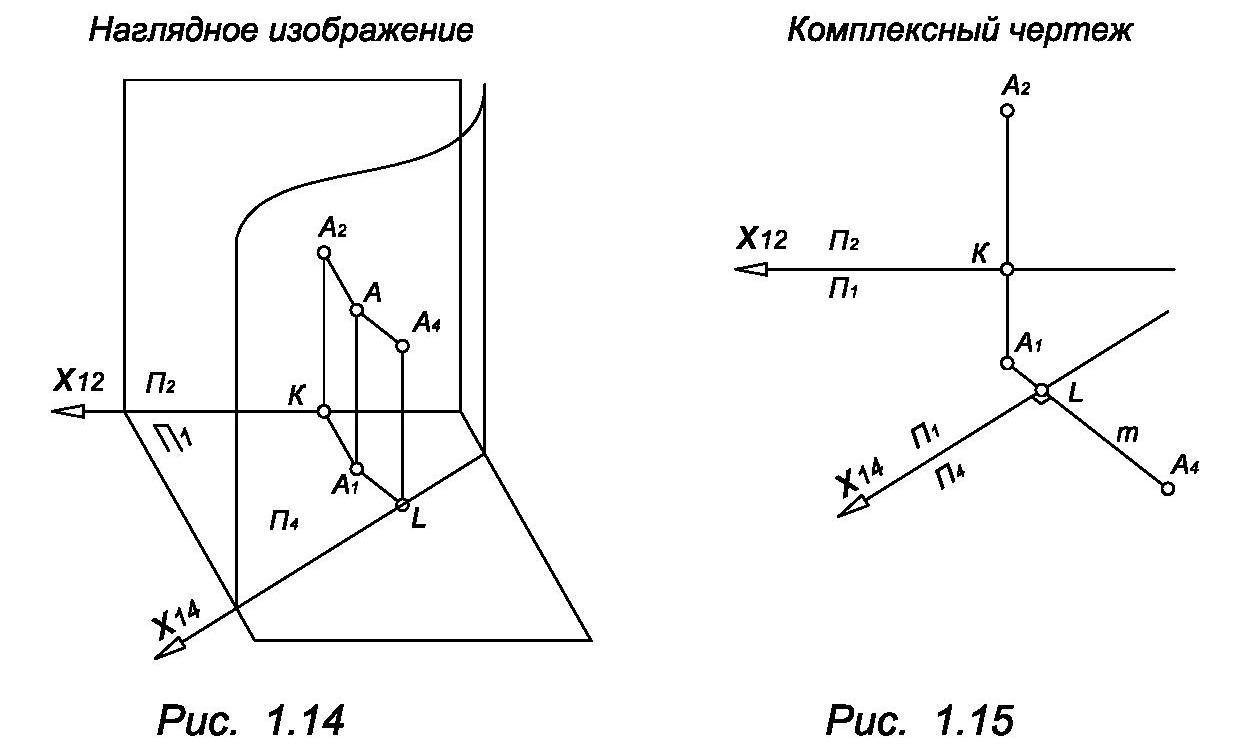
А – точка в пространстве. А₁ и А₂ соответственно горизонтальная и фронтальная проекция точки А. А₄ – проекция точки А на плоскость П₄, т.е. дополнительная проекция точки А. K и L точки на проекционных осях.

Из чертежа видно, что А₂КА₁А и А А₁LА – прямоугольники следовательно, /А₂К/ = /АА₁/ = /А₄L/. Проецирование ортогональное, значит прямые А₁L, А₄L, и X₁₄ взаимно перпендикулярны. Пользуясь этими свойствами, легко построить дополнительную проекцию на комплексном чертеже (см. рис. 1.15).

При построении дополнительной проекции точки целесообразно пользоваться следующим алгоритмом:

1. Выбирается дополнительная плоскость проекций П₄. П₄ перпендикулярна одной из данных плоскостей проекций, на нашем чертеже П_{4 ┴} П₁. П₄П П₁ – X₁₄, прямую X₁₄ назовем новой осью проекций.

2. Через проекцию точки А₁ следует провести новую линию проекционной связи m, m _┴ X₁₄.

3. На этой линии от точки L следует отложить отрезок LA₄, / LA₄/ = /А₂К/. А₁ – дополнительная проекция точки А.

Особого внимания заслуживает случай, когда дополнительная проекция перпендикулярна к плоскостям П₁ и П₂ (рис. 1.16).

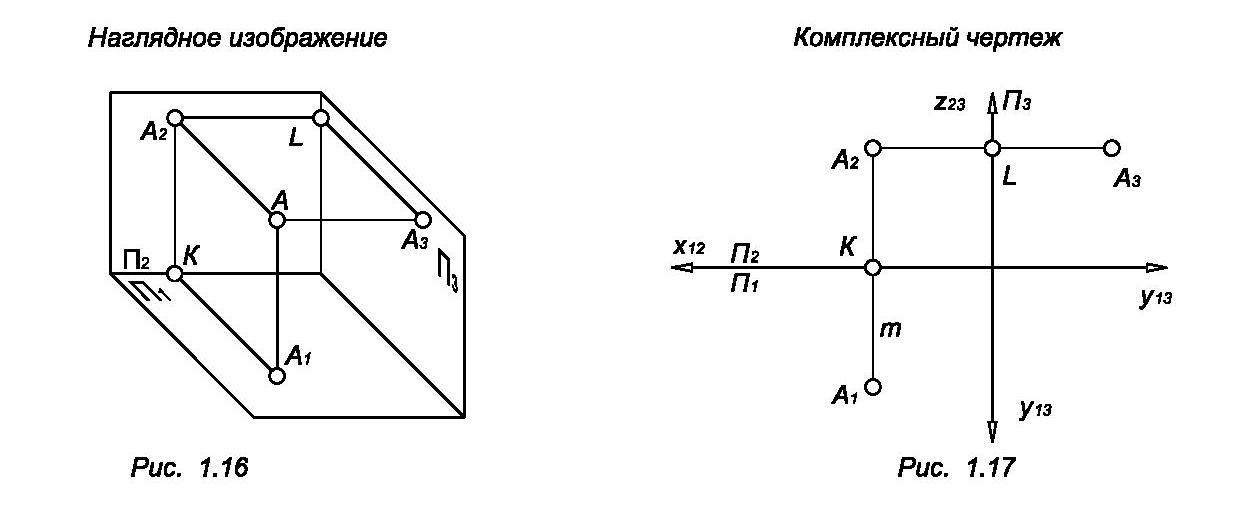
В черчении изображение на плоскости П₃ относится к основным видам. Плоскость П₃ называется профильной плоскостью проекций. А₃ – профильная проекция точки А. Чтобы построить А₃ по данным А₁ и А₂ следует выполнить такие действия:

1. Провести линию проекционной связи А₂L, А₂L _┴ Z₂₃ (рис. 1.17)

2. Отложить на этой линии от оси Z₂₃ отрезок LА₃, / LА₃/ = / КА₁/.

Для решения более сложных задач метод замены плоскостей проекций можно применять неоднократно. Этот метод наряду с другими методами геометрического моделирования применяется во многих областях науки и техники. С помощью метода замены плоскостей проекций можно решать почти 90% задач нашего курса. Иногда мы пользуемся этим методом неосознанно, выделяя частные случаи на более общих в той или иной теории.