Методические материалы / Методичка по так называемому четвертому звену

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

"Ярославский государственный технический университет"

Кафедра кибернетики

Н. Н. Василькова

Методичка по так называемому четвертому звену

(из задания на курсовой проект по ТАУ)

2007

Методичка по так называемому четвертому звену

(из задания на курсовой проект по ТАУ)

Вывод уравнения переходной функции для звена с передаточной

функцией вида

Так как запаздывание только сдвигает переходную функцию, на время τ, то вывод переходной функции будем делать для аналогичного звена без запаздывания, а “τ” - учтем в оконча­тельной формуле.

Итак,

Рассмотрим 1-ый случай, когда корни характеристического уравнения звена действительные и разные.

Характеристическое уравнение

Выражение для корней

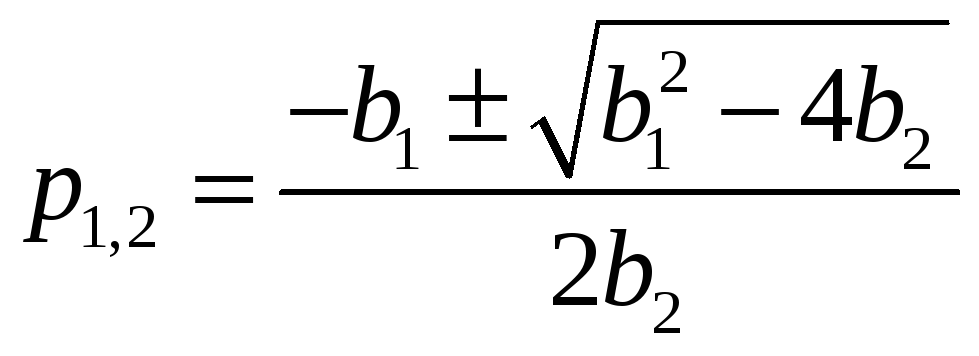
Или

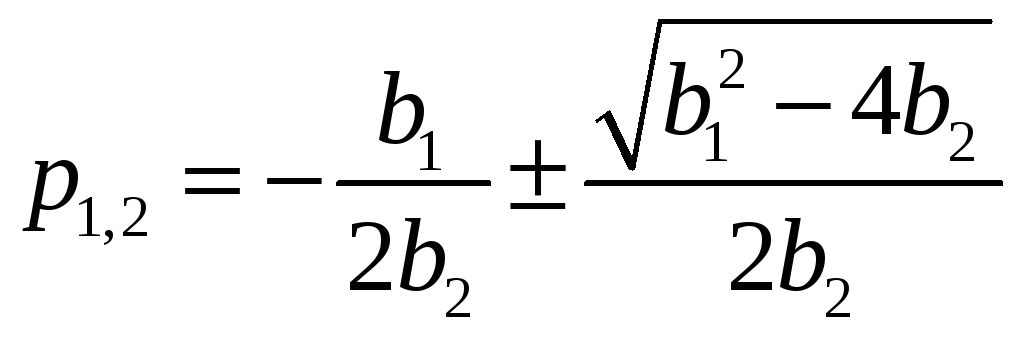
Корни будут действительные и разные, если дискриминант , а это будет, если , или

Если корни характеристического уравнения действительные и разные , то характеристический полином можно разложить на множители

Причем попутно проанализируем, чему равно произведение корней

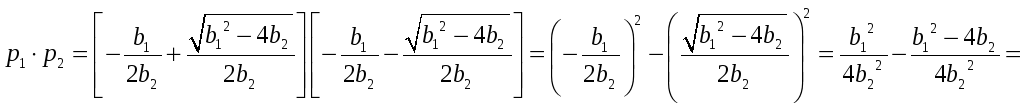
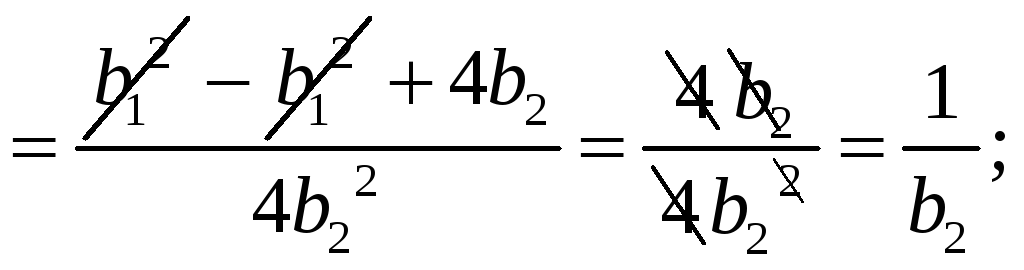
Таким образом, или

Это соотношение пригодится несколько позднее, при преобразовании уравнения переходной функции к виду, приведенному в методичке.

Переходим непосредственно к выводу переходной функции. Итак,

или

Разлагаем изображение на простые дроби:

При (I)

При (2)

При (3)

Из (3) или с учетом доказанного, что

Подставим А в (1) и (2), получим

(4)

(5)

Из (4) (6)

Подставим (6) в (5)

(7)

Подставим теперь (7) в (6) и выразим С:

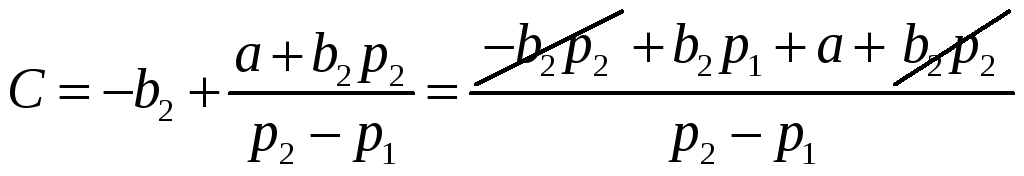
(8)

Итак, выражения для коэффициентов разложения на простые дроби А, В, С мы нашли, можно искать оригинал переходной функции по изображению, приведенному к виду суммы трех простых дробей

;

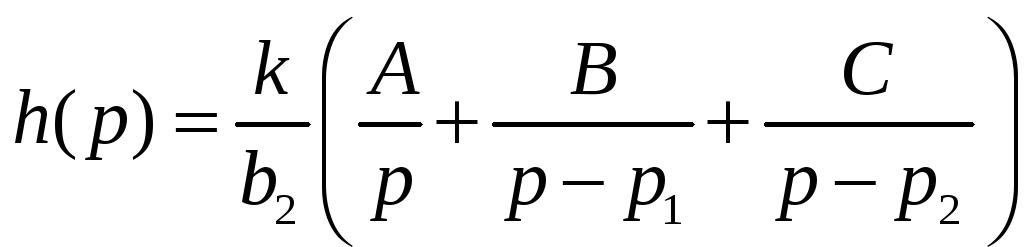Оригинал будет:

; (9)

Подставим в (9) выражения для А, В, С →

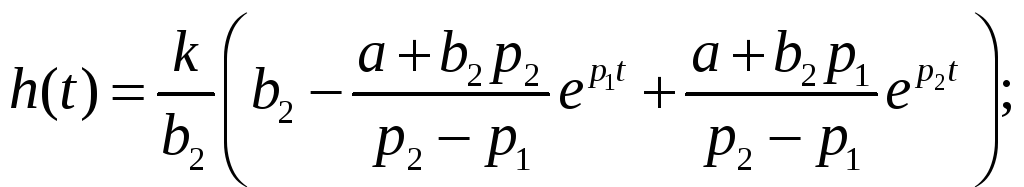
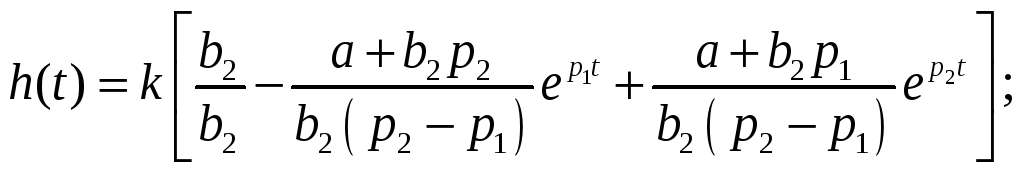
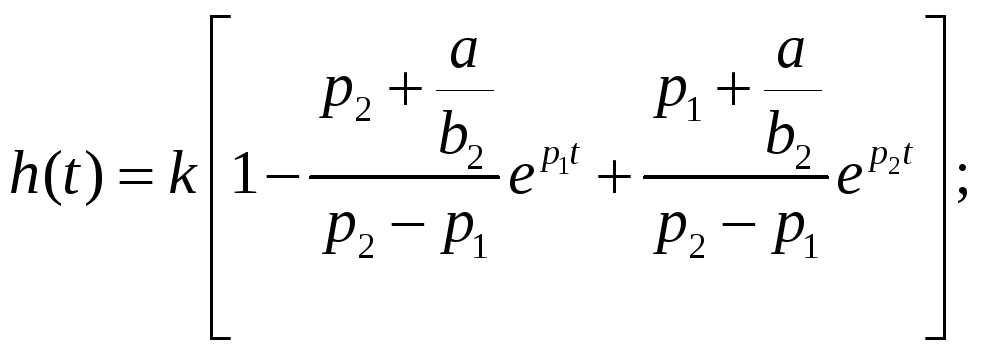
Теперь осталось только учесть явление транспортного запаздывания в виде запаздывающего аргумента, т.е. при расчет вести по формуле

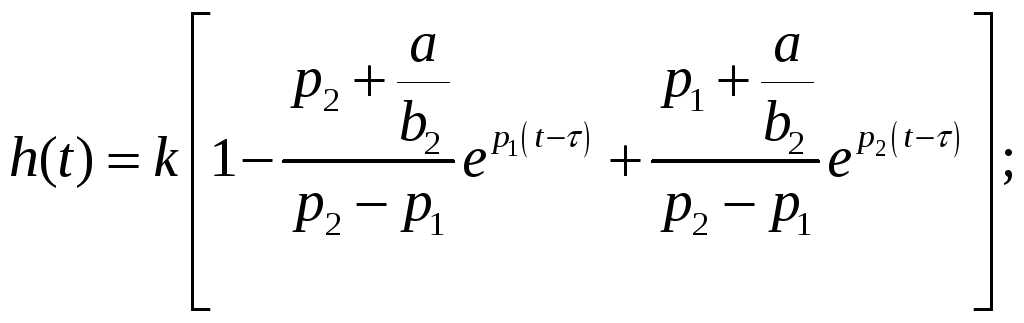(10)

Что и требовалось доказать!

Не забыть, что при наличии запаздывания при , Т.е. расчет по формуле (10) можно вести для моментов времени

Рассмотрим 2-й случай, когда корни характеристического уравнения действительные и равные.

Это будет, когда дискриминант в выражении для корней (см. cтр. 1) равен 0, т.е. когда ;

или или при

В этом случае корни т.е.

Поскольку корни равны, их часто обозначают одинаково

, т.е. в этом случае.

В этом случае характеристический полином можно разложить на такие множители:

а доказанное соотношение примет вид

Ищем переходную функцию по изображению , которое в этом случае примет вид:

Разложим изображение на простые дроби:

При (11)

При (12)

При (13)

Из (13) → (14) или (15)

Из (11) → или (16)

Или (17)

Из (12) →

Или, подставляя. А, получим

(17)

Подставим А, В, С в изображение

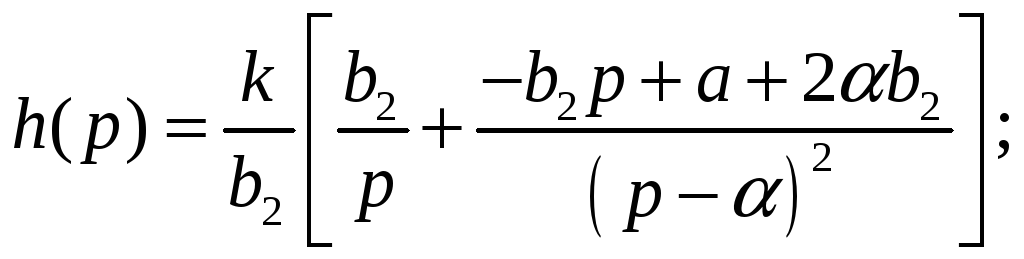
Преобразуем

Или

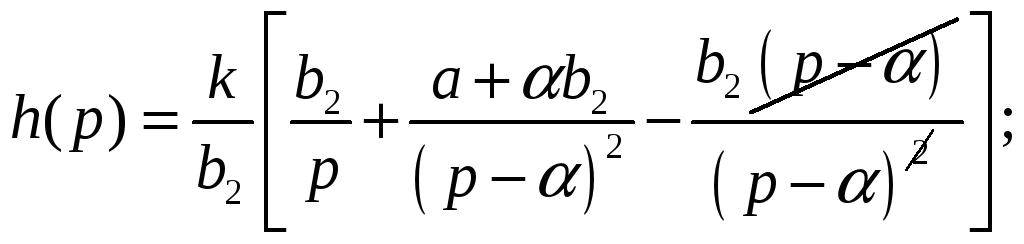
Или

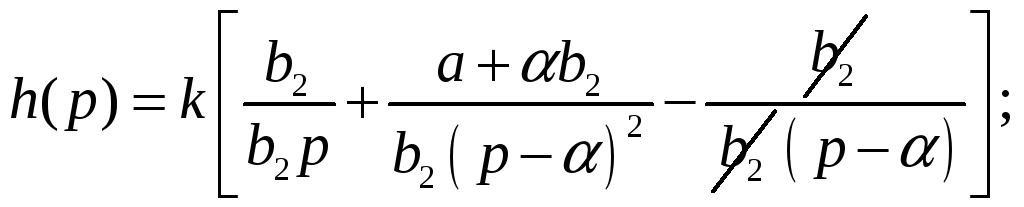
Ищем оригинал по изображению

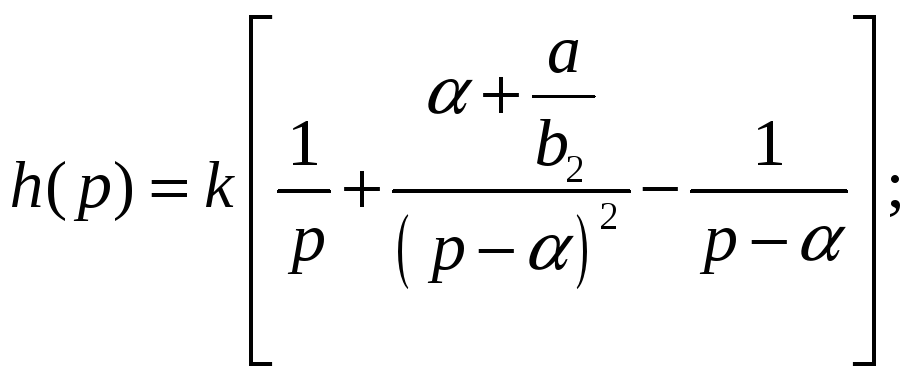
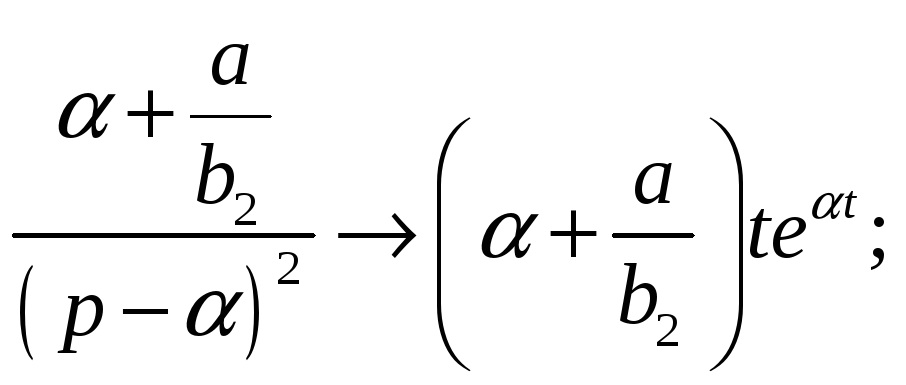
Таким образом

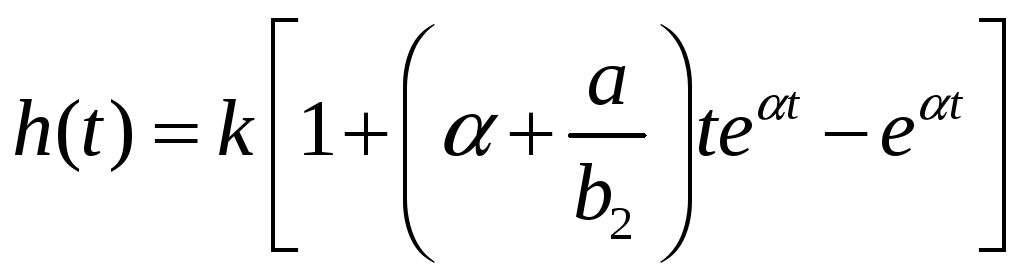
Или

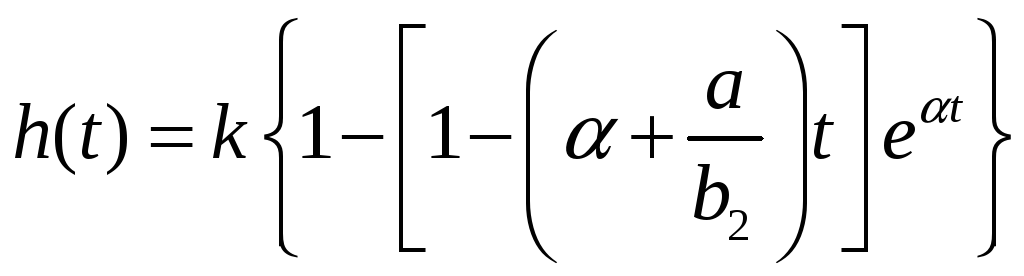
Учитывая теперь транспортное запаздывание, получим окончательно

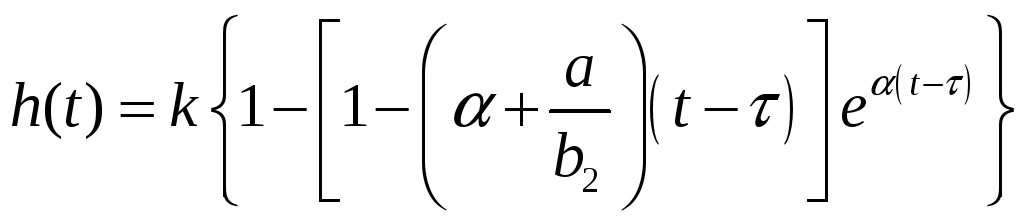(18)

Следует помнить, что уравнение (18) имеет смысл при , а при

Рассмотрим 3-й случай, когда у звена c передаточной функцией вида

корни характеристического уравнения получаются комплексными сопряженными.

Рассмотрим сначала, при каких условиях это возможно. Общее выражение для корней имеет вид:

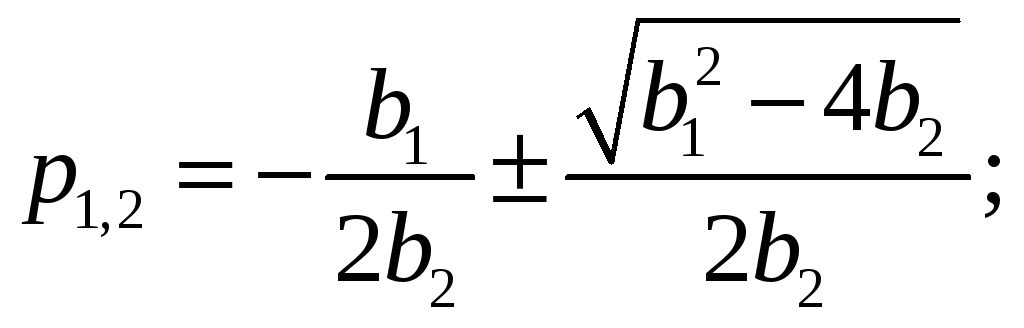
Из него видно, что корни будут комплексными, если дискриминант будет отрицательным, т.е. , т.е. при

или при .

В этом случае выражение для корней можно переписать:

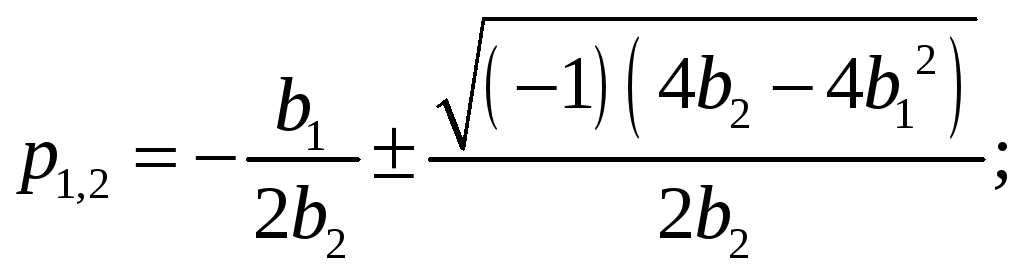
Или , где (19) (20)

Выведем уравнение переходной функции для звена

(т.е. без учета запаздывания).

Разложим на простые дроби.

(Примечание: в этом случае, поскольку корни комплексные, то полином уже нельзя разложить на два вещественных полинома 1-й степени)

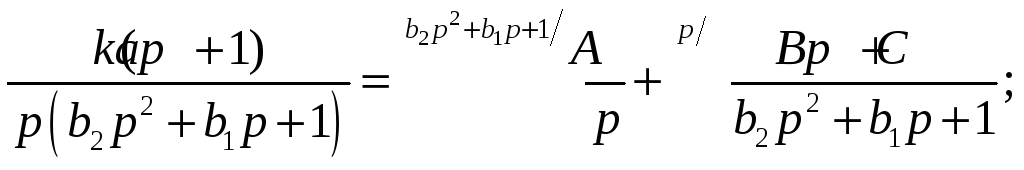
(можно делать вывод без сомножителя "К", а потом его учесть в конечном выражении)

При (21)

При (22)

При (23)

Подставим (23) в (21), получим (24)

Подставим (23) в (22), получим:

(25)

Подставим А, В, С в изображение

Ясно, что оригинал для слагаемого будет . По­этому рассмотрим второе слагаемое и преобразуем его.

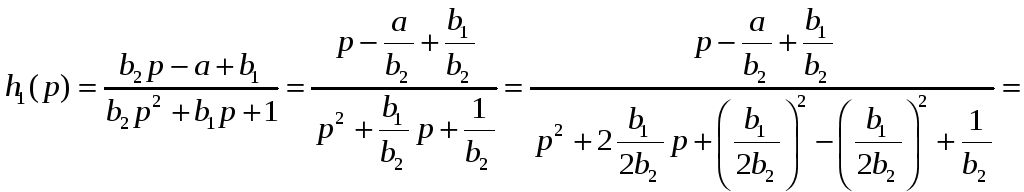
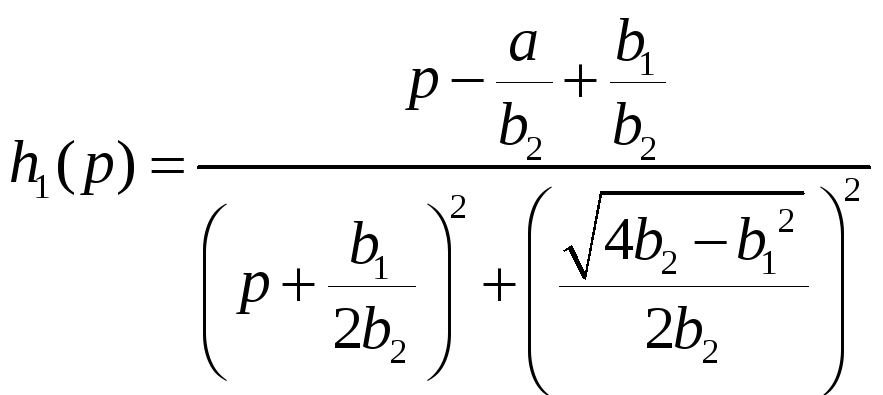
Если мы вспомним выражение для действительной части корней xapaктеристического уравнения (19) и выражение для мнимой части корней

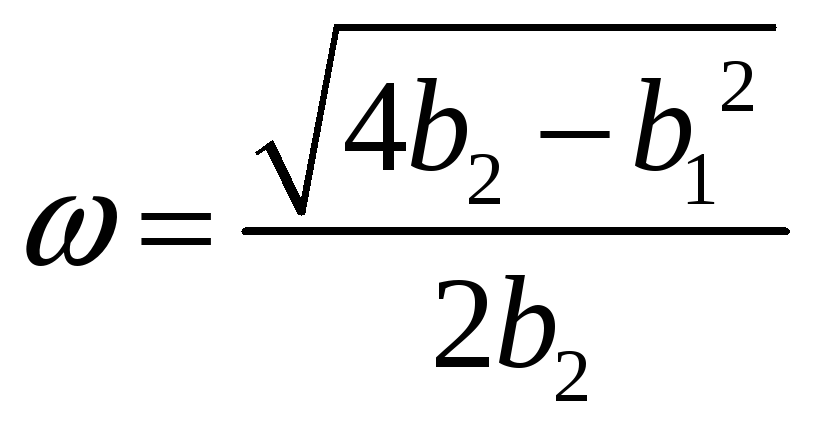(20)

то нетрудно заметить, что в знаменателе выражения (26) мы полу­чили и α, и ω. Поэтому перепишем выражение (26) так

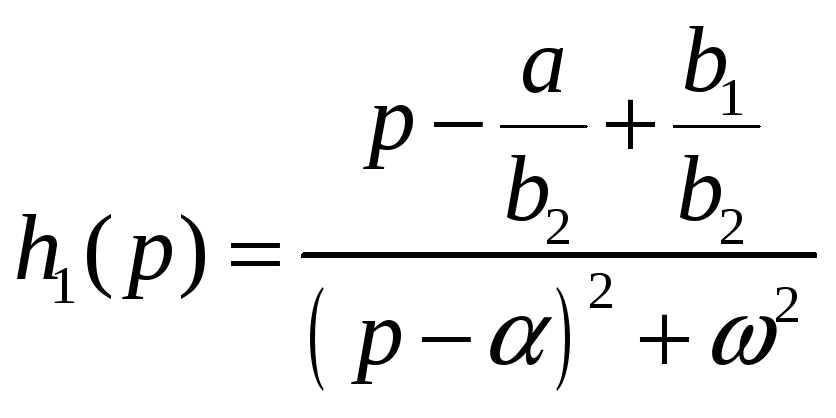(27)

Теперь преобразуем числитель выражения (27)

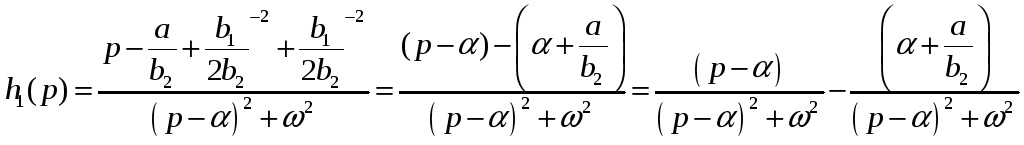
Чтобы преобразовать второе слагаемое к табличному виду, умножим и разделим его на ω: Т.о.

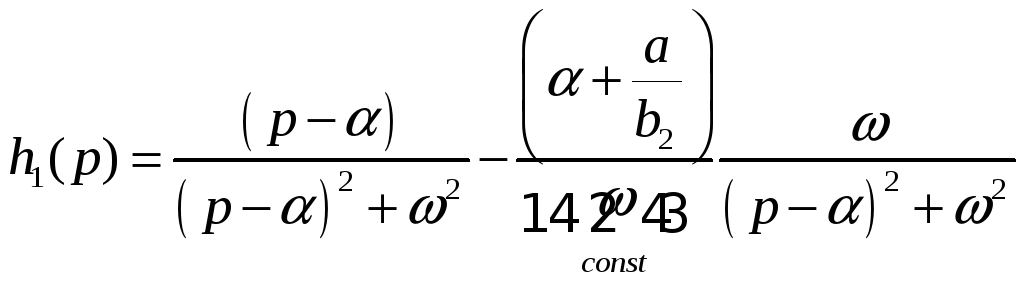
Теперь для можно найти оригинал по таблицам преобразования Лапласа;

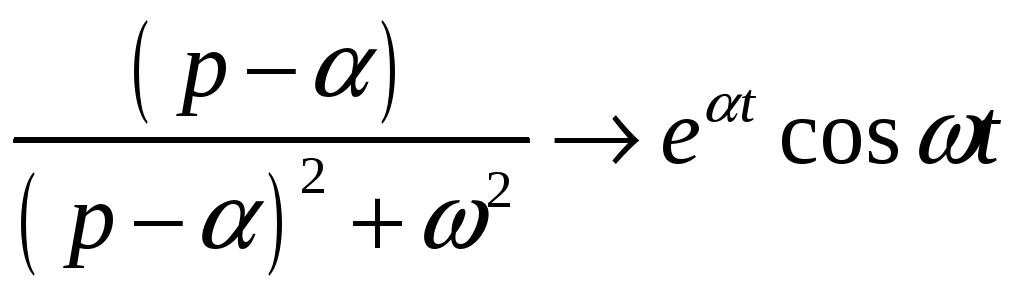(29)

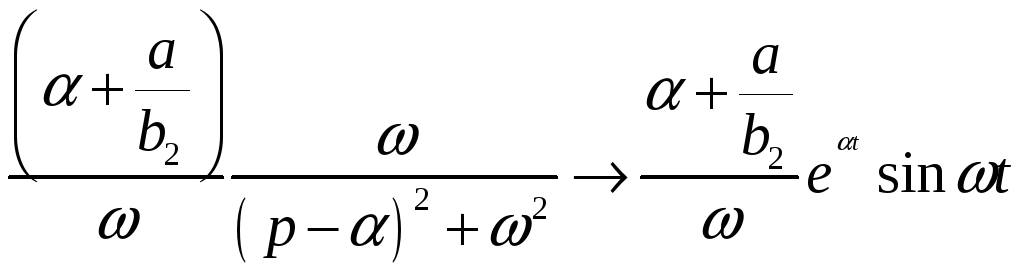(30)

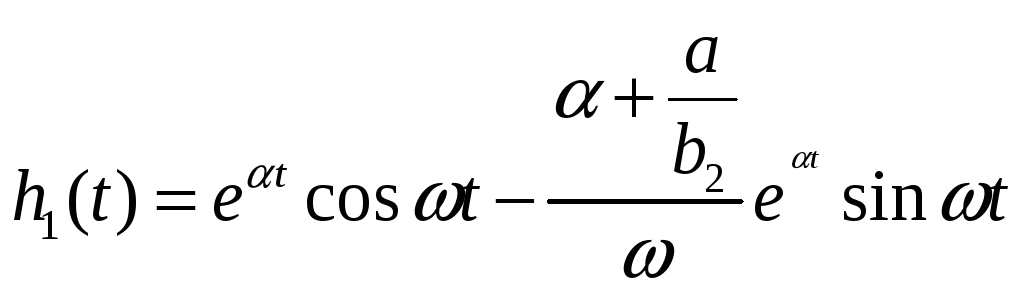
Теперь, вернувшись на стр. 12, найдем оригинал как сумму оригиналов, т. е.

Или

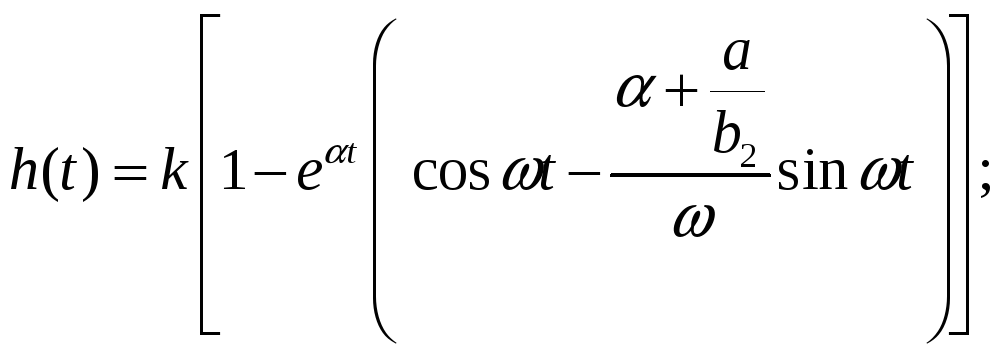
И, окончательно, с учетом транспортного запаздывания (которое было отброшено в начале вывода) получим:

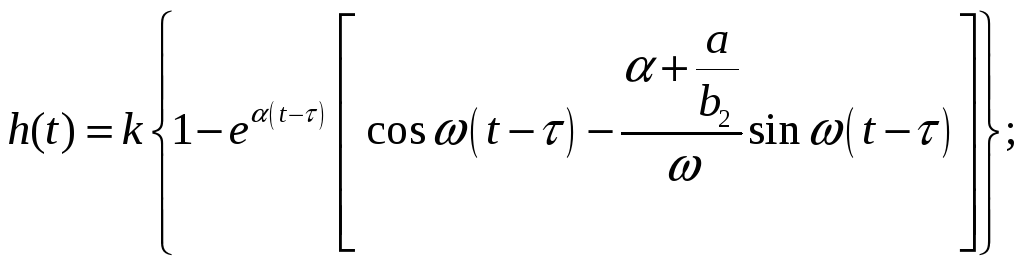
что справедливо при , а при .