Метод.указ Мех.материалов и ОК

A = 3а × 2а = 6а2

= 6×202

= 2400 мм2;

2

IxII

= 32 ×104 + (-3,1)2 2400 = 731864 мм4.

c

Момент инерции сечения круга III относительно оси xс:

I III

= I

x

+ a

2 A ;

x

3

3

c

c3

Ixc

= p d 4 / 64 = 3,14 ×204 / 64 = 7850 мм4;

3

a3 = y3 - yc

= 20 - 23,1 = -3,1 мм;

A = p d 2 / 4 = 3,14×202 / 4 = 314 мм2;

3

IxcIII = 7850 + 3,12 ×314 = 61735 мм4.

Величина момента инерции сечения относительно оси xс

Ix

= 417132 + 343064 -10867 = 749329 мм4.

c

5. Момент инерции сечения относительно оси ус

I y

= I yI

+ I yII - I yIII ,

c

c

c

c

где I yI ,

I yII ,

I yIII - моменты инерции простых сечений I, II, III относи-

c

c

c

тельно оси ус.

Момент инерции I ycI рассчитываем по формуле

I I

= I

y

+ b 2 A .

y

1

1

c

c1

Момент инерции прямоугольникаI относительно собственной

центральной оси yс

1

I yc = h· b3 / 12 = 3a ×a3 / 12 = а4 / 4 = 4×104 мм4.

1

и yс

Расстояния между осями yс

b1 = x1 - xc

1

=10 - 44, 7 = -34,7 мм.

Площадь прямоугольника I

A =1200 мм2.

1

Величина момента инерции относительно оси ус

I ycI = 4 ×104 + (-34,7)2 ×1200 =1484908 мм4 .

Аналогично для прямоугольника II:

I II

= I

y

+ b

2 A ;

y

c

2

2

c 2

= 4,5×204 = 72×104 мм4;

I y

c 2

= hb3 / 12 = 2a ×(3a)3 / 12 = 4,5а4

b2 = x2 - xc = 60 - 44,7 =15,3 мм.

II

= 7210

4

+ (15,3)

2

×

4

I yc

2400 =1281816 мм .

21

Момент инерции круга относительно оси yс:

I III

= I

y

+ b 2 A ;

y

c

3

3

c3

I y

c3

= p d 4 / 64 = 3,14 ×204 / 64 = 7850 мм4;

b3 = x3 - xc

= 60 - 44,7 =15,3 мм;

A = p d 2

/ 4 = 3,14 ×202 / 4 = 314 мм2;

3

I ycIII = 7850 +15,32 ×314 = 8135 мм4.

Величина момента инерции сечения относительно оси yс

I yc

=1484908 +1281816 - 81354 = 2685370 мм4.

Полярный момент инерции сечения

I p

= Ix

+ I y

c

= 749329 + 2685370 = 3434699 мм4.

c

6. Центробежный момент инерции сечения

Ix

С

y

С

= IxI

y

C

+ I xII

y

С

- I xIII y

,

C

C

C

C

где IxI

C

y

C

,

I xII

y

,

I xIII y

– центробежные моменты инерции простых се-

C

C

C

C

ус . Центробежный момент

чений I,

II,

III

относительно

осей xс ,

инерции прямоугольника I относительно осей xс , ус

I I

= I

xC

yС

+ a b A .

xC yC

1

1 1 1

Оси xc

и yc

1

являются осями симметрии прямоугольникаI, по-

1

1

этому IxС

1

yС

= 0 . Ранее найдены a1 = 6,9 мм; b1 = -34,7 мм; А1 =1200

1

м2. После подстановки получим

IxII

y

= 0 + 6,9(-34,7)1200 = -287316 мм4.

СС

Аналогично центробежный момент инерции прямоугольникаII относительно осей xс , ус .

Оси xc			и yc	являются осями симметрии прямоугольникаII, по-
этому IxС	2		2	Ранее определили a2				= -13,1 мм; b2 =15,3 мм;
	y	С	= 0 .
	2		2
A = 2400 мм2. После подстановки получим
2					= 0 + (-3,1)×15,3×2400 = -113832 мм4.
			IxII	y
			С		С
Центробежный момент инерции круга относительно осей xс , ус
					I III	= I	+ a b A .
					xС yС		xС 3 yС 3	3 3 3

Оси xc3 и yc3 являются осями симметрии круга III, поэтому

22

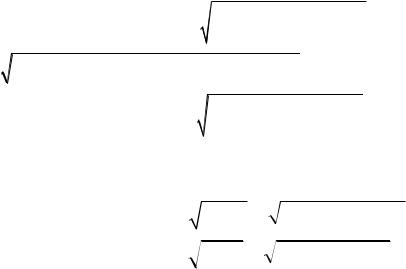
I	= 0 . Ранее определили a = -3,1 мм;					b =15,3 мм ;	A = 314 мм2.
	xС 3 yС 3				3	3	3
После подстановки получим
				IxIIIy	= 0 + (-3,1)×15,3×314 = -14893 мм4.
				С	С
	Центробежный момент инерции сечения
	Ix	C	y	= -287316 -113832 - (-14893) = -386255 мм4.
				C

7. Угол поворота центральных осей, определяющих положение центральных главных осей:

a = arctg(IxC yC / (I yC - IxC )) = arctg(-386255 / (2685370 - 749329)) = -8, 42°.

Знак минус показывает, что систему координат xc , С, yc нужно повернуть по часовой стрелке на уголa и получить оси u и v – главные центральные оси инерции сечения.

8. Определим главные центральные осевые моменты инерции

Iu =Imax =I1 =0,5(Iyc

+Ixc

)+

é

-Ixc

ù2

2

=0,5(2685370+749389)+

ë0,5(Iyc

)û

+Ixcyc

+ (0,5(2685370-749389))2 +(-386255)2 =1717349,3+1042236,6=2759586 мм4.

I

=I

=I

=0,5(I

yc

+I

xc

)-

é0,5(I

yc

-I

)ù2

+I2

=1717349,3-1042236,6=675113 мм4.

v

lim

2

ë

xc

û

xc yc

9. Главные центральные радиусы инерции:

ru = Iu / A = 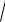2759586 / 3914 = 26,6 мм; rv = 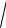I v / A = 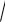675113 / 3914 =13,1 мм.

4. ИЗГИБ СТЕРЖНЕЙ (БАЛОК)

Задание 4. Для балки на двух опорах, нагруженной сосредоточенной силой F, распределённой нагрузкой интенсивностью q и изгибающим моментом M (рис. 8), рассчитать размеры следующих поперечных сечений: а) прямоугольника; б) квадрата; в) круга; г) швеллера; д) двутавра.

Сравнить массы балок с поперечными сечениями этой формы. Значения силовых факторов и размеров приведены в табл. 4. Допус-

каемые напряжения изгиба [s ] =150 МПа.

23

Указания по выполнению задания

1.Определить из условия статического равновесия реакции в опорах балки.

2.Применяя метод сечений для каждого участка балки, построить эпюры внутренних силовых факторовизгибающего момента М и поперечной силы Q.

3.Определить максимальный изгибающий момент на эпюре М.

Из условия прочности на изгиб: s = M max / Wx £ [s ], найти геометрический параметр поперечного сечения – момент сопротивления сечения Wx ³ M max / [s ].

Таблица 4

Исходные данные к заданию 4

Параметр		Числовые значения параметров по вариантам
	1		2	3	4	5	6	7	8	9		10
F, кН	20		25	30	35	40	45	50	55	60		65
q, кН/м	100		200	50	150	120	80	140	160	180		60
M, кH м	10		5	8	7	6	9	12	14	15		16
l, м	0,2		0,4	0,1	0,3	0,5	0,1	0,2	0,3	0,4		0,5

4.В зависимости от формы сечения балки по величине Wx определить размеры сечения. Для прямоугольного сечения принять h = 2b .

5.Из условия mi / mk = Ai /Ak найти соотношения масс балок для разных геометрических форм поперечных сечений.

6.Рассчитать максимальные касательные напряжения для различных форм поперечных сечений. Сравнить их с допускаемыми напряжениями.

24

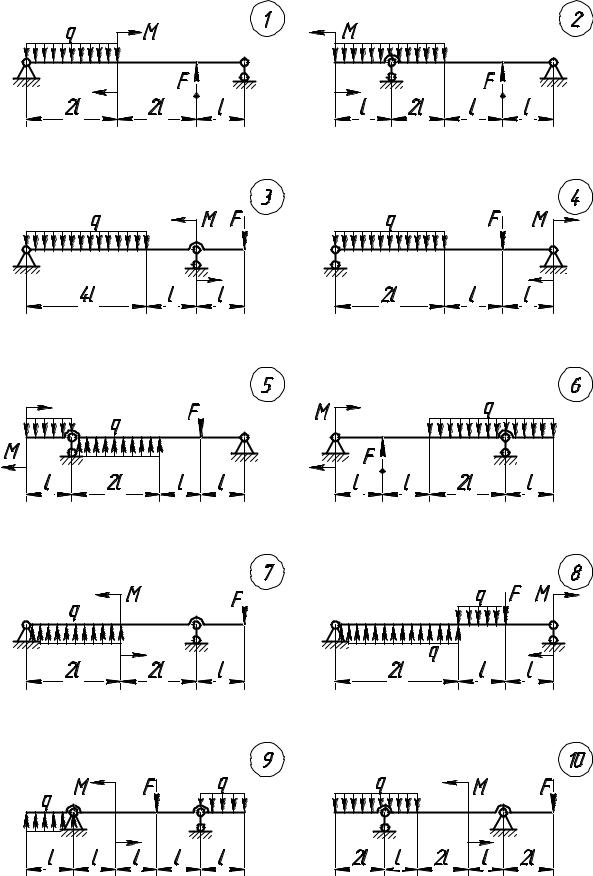
Рис. 8. Расчетные схемы к заданию 4. В кружках – номера вариантов

25

ПРИМЕР РАСЧЁТА

Балка опирается на две опоры и нагружена сосредоточенной силой F = 40 кН, распределённой нагрузкой интенсивностью q =100 кН/м, согласно схеме на (рис. 9, а). Рассчитать размеры поперечных сечений следующей формы: а) прямоугольника; б) круга; в) швеллера; г) двутавра, если допускаемые напряжения [s ] =120 МПа, а длина l = 0, 2 м. Сравнить массы балок с поперечными сечениями разной формы.

Решение

1. Отбросим опоры, а их действие на балку заменяем опорными реакциями YА и YВ . Определяем реакции опор из условия статического равновесия балки:

åM A = F ×l - q ×2l ×0,5×2l +YВ ×2l + M ;

YВ = (-F ×l +2q ×l2 -M) / (2l) = (-40×0,2 + 2×100×0,22 -6) / (2×0,2) = -15 кH.

Знак минус показывает, что реакция опоры B направлена в противоположную сторону от первоначально выбранного направления. Изменим на противоположное направлениеYВ на расчётной схеме (рис. 9, б). Знак плюс показывает, что направление этой реакции соответствует выбранному первоначально.

Проверка: åУi = -F +У А - q × 2l -YВ = - 40 + 95 -100 ×0, 4 -15 = 0.

Реакции опор определены правильно.

2. Построим эпюру внутреннего силового фактора– изгибающего момента. Разбиваем балку вдоль продольной оси на силовые участки. Границами участков являются границы балки и сечения, в которых приложены внешние силовые факторы. В нашем случае таких участков три. Мысленно выполним сечение на первом силовом участке.

Из условия статического равновесия отсечённой части определим значение внутреннего силового фактора – изгибающего момента на первом участке (рис. 9, в). Правило знаков при составлении уравнения и построении эпюр приведено на (рис. 10).

Введём переменную координату z1 на первом участке, 0 £ z1 £ l

-Fz1 - M1 = 0; M1 = -Fz1 ,

26

при z1 = 0 M1 = 0;

при z1 = l M1 = -F ×l = -40 ×0, 2 = -8 кН м.

График изменения изгибающего момента представлен прямой (рис. 9, е). В дальнейшем будем пропускать уравнение равновесия для мысленно отсечённого участка балки и сразу записывать выражение для изгибающего момента в соответствии с принятым правилом знаков:

åМ В = F ×3l + q × 2l ×0,5 × 2l -YА × 2l + M = 0;

Y = (F ×3l

+ 2q ×l2 + M) / (2l) = (40×3×0,2 + 2×100 ×0,22 +6) / (2 ×0,2) = 95 кН.

А

На втором участке переменная координата z 2 , 0 £ z2 £ 2l

(рис. 9,

г). Для отсечённого участка балки М

2

= -F(l + z

) +У

А

× z

2

- q × z2

/ 2;

2

2

при z2

= 0

M

= -F ×l = -40 ×0, 2 = -8 кН·м;

при z

2

= 2l

M

2

= -F ×3 ×l +Y × 2 ×l - q(2 ×l)2 / 2 = -40 ×3 ×0, 2 + 95 ×2 ×0, 2 -

А

-100

×0,42 / 2 = 6 кН·м.

График изменения изгибающего момента на втором участке представлен параболой, так как переменная z2 в квадрате. На треть-

ем участке переменная координата z3 , 0 £ z3 £ l (рис. 9, д). Для отсечённого участка балки

M 3 = -F (3l + z3 ) + YА (2l + z3 ) -YВ × z3 - q ×2l ×(0,5 ×2l + z3 );

при z3 = 0 M3 =-F ×3l +YА ×2l -q×2l2 =-40×0,6+95×0,4-100×2×0,22 =6 кН·м;

при z3 = l

M3 =-F×4l +YА ×3l -YВ ×l -q×4l2 =-40×4×0,2+95×3×0,2-15×0,2-100×4×0,22 =6

кН·м. Эпюра на третьем участке представлена прямой линией, параллельной базисной (рис. 9, е).

3. Построим эпюру поперечной силы. Для этого воспользуемся

методом	сечений. Для отсечённой на		первом	участке части балки
(рис. 9,	в) условие равновесия	имеет	видåYi	= 0; -F - Q1 = 0;
Q1 = -F - 40 кН. Направление Q1		не соответствует первоначально за-

данному и согласно правилу знаков(рис. 14) является отрицательным. Эпюра на этом участке представлена прямой, параллельной базисной линии эпюры.

Мысленно отсечём часть балки на участке II (рис. 9, г). Запишем сразу выражение для поперечной силы на втором участке, 0 £ z2 £ 2l

27

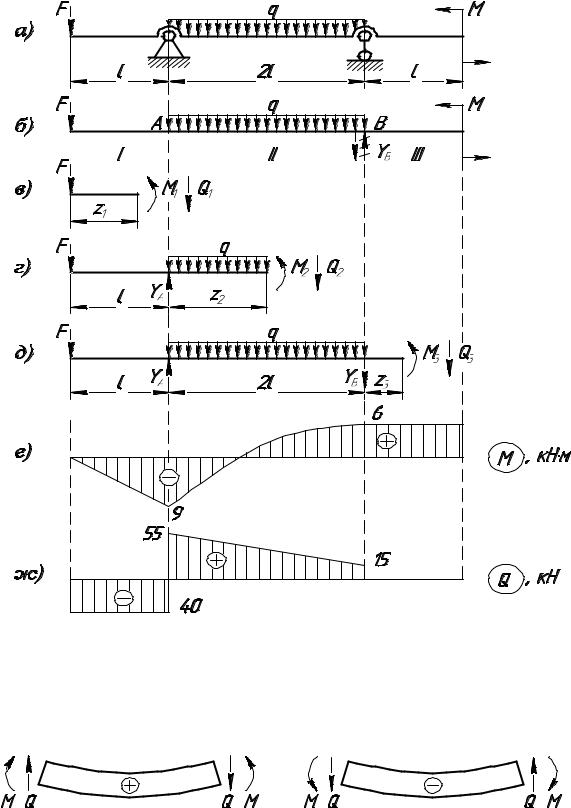
Q2 = -F + YА - q × z2 ;

при z2 = 0 Q2 = -F + YА = -40 + 95 = 55 кН;

при z2 = 2l Q2 = -F +У А - q ×2l = -40 + 95 -100 ×2 ×0,2 =15 кН;

Рис. 9. К расчёту балки на изгиб: а – расчётная схема балки; б – схема реакций опор; в, г, д – схемы определения М и Q на силовых участках; е – эпюра изгибающих моментов М; ж – эпюра поперечных сил Q

28

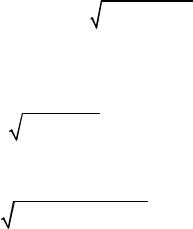
Рис. 10. Правило знаков при построении эпюр М и Q

График изменения Q на втором участке представлен наклонной прямой. Отсечение части балки на третьем участке(рис. 9, д) приводит к следующему выражению:

Q3 = -F +YА - q × 2l -YВ = -40 + 95 -100 × 2 ×0,2 -15 = 0 .

На участке III поперечная сила отсутствует (рис. 9, ж). 4. Запишем условие прочности балки при изгибе

s = M max / Wx £ [s ],

где Mmax – максимальный изгибающий момент, M max = 8 кН·м; Wx – момент сопротивления поперечного сечения, зависящий от его формы и размеров; [s ] – допускаемое напряжение, [s ] =120 МПа =

=120 Н/мм2.

Момент сопротивления сечения

Wx ³ M max / [s ] = 8 ×106 / 120 = 66, 7 ×103 мм 3 = 66,7 см 3 .

Для прямоугольного поперечного сечения при h = 2b получим

W = b ×h2 / 6 = b(2b)2	/ 6 = 2b3 / 3 ³ 66,7 см 3 , b = 3 (3×66,7) / 2 = 4,65 см.
x	h = 2b = 2 × 4, 65 = 9,3 см.
Площадь сечения:	A = h ×b = 9,3× 4,65 = 43, 2 см 2 .
Для квадратного поперечного сечения b = h
W = b3 / 6 ³ 66,7 см 3 , b = 3						= 7,37 см.
				(6 ×66, 7)
x	А = b2 = 7,372 = 54,3 см2.
Площадь сечения:
Для круглого поперечного сечения
W = p ×d 3 / 32	³ 66,7 см 3 , d = 3						= 8,79 см.
			(32 ×66,7 / 3,14)
x
Площадь сечения A = p × d 2 / 4 = 3,14 ×8,792 / 4 = 60, 7 см2.
Для швеллера №14 W = 70,2		см3 > 66,7			см3 , площадь его сече-
ния А =15,6 см2.	x
Для двутавра №14 Wx = 81,7		см3 > 66,7			см3 , площадь его сече-
ния А =17, 4 см2.

5. Примем площадь швеллера анализа масс балок с различными получим следующее отношение масс и одинаковой длины mi / mш = Ai / Aш :

за единицу для сравнительного поперечными сечениями. Тогда для балок из одного материала

29

-для прямоугольника An / Aш = 43,2 / 15,6 = 2,77 ;

-для квадрата Aкв / Aш = 54,3 / 15,6 = 3,48;

- для круга Aкр / Aш = 60,7 / 15,6 = 3,89 ;

- для двутавра Aд / Aш =17,4 / 15,6 =1,12 .

Наименьшую материалоёмкость при изгибе обеспечивают тонкостенные сечения – швеллер и двутавр, наибольшую – круг.

6.Рассчитаем значения касательных напряжений, возникающих

вэтих сечениях, и сравним их с допускаемыми. Допускаемые каса-

тельные напряжения: [t ] = 0,6[s ] = 0,6 ×120 = 72 × МПа = 72 Н/мм2 .

Максимальные касательные напряжения определяем по формуле Журавского

t = (Q × Sxотс ) / (b × Ix ),

где Q – максимальная поперечная сила, Q = 55 кН, Sхотс - статический момент отсечённой площади, b – ширина поперечного сечения, Ix – момент инерции поперечного сечения.

Для прямоугольника

t = [Q × 0,5b(h2 / 4)] / (b × h3 / 12) = (3 / 2)[Q / (b × h)] = (3 / 2)(Q / A) =

= (3 / 2)[(55 ×103 ) / (43,2 ×102 )] =19 Н/мм2 < [t ] = 72 Н/мм2.

Для квадрата

t = (3 / 2)(Q / A) = (3 / 2)[(55×103 ) / (54,3×102 )] =15H / мм2 <[t ] = 72 Н/мм2..

Для круга

t = (4Q) / (3p × R2 ) = (4Q) / (3A) = (4 ×55×103 ) / (3×60,7 ×102 ) =12 H/мм2 <[t].

Для швеллера

t = (Q × S xот с ) / (b × I x ) = (55 ×103 × 40, 8) / (0, 49 × 491) = 9327 Н/см2 = = 93,3 Н/мм2 > [t ] = 72 Н/мм2.

Действующие касательные напряжения превышают допускаемые. Для двутавра

t = (Q × Sxотс ) / (b × Ix ) = (55 ×103 × 46,8) / (0,49 ×572) = 9183 H/ñì 2 = = 92 H/мм2 > [t ] = 72 H/мм2 .

Действующие касательные напряжения превышают допускаемые. Поскольку касательные напряжения в швеллере и двутавре пре-

вышают допускаемые значения, применение этих тонкостенных сечений не возможно. Нужно выбрать сечения с большими значениями

30