ГЛ 9

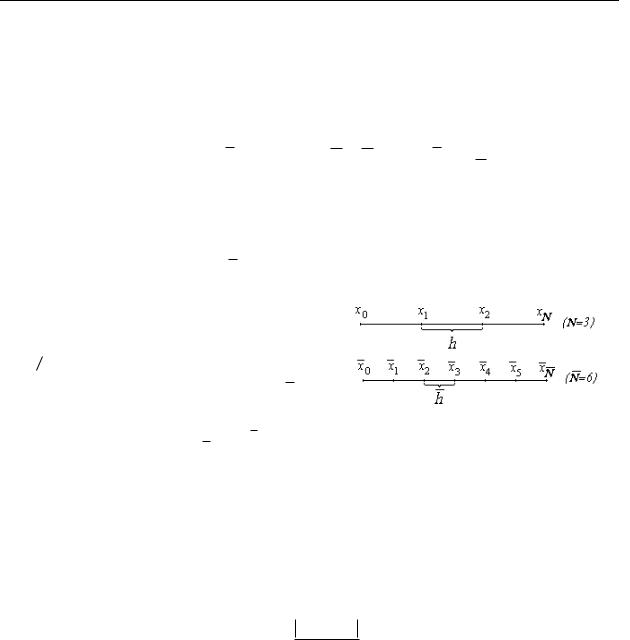
Глава 9. Численные методы решения обыкновенных дифференциальных	88
уравнений

Используем для приближённого решения задачи Коши (9.1.1) вычислительную схему, имеющую порядок точности k. Построим на отрезке [a ;b] две сетки: {xn} и {xn} . Вторую сетку получим из первой путём сгущения в 2 раза:

xn =a +n h , n =0,1, , N ,

xn =a +n h , n =0,1, , N ,

h = (b −a) ;

N

N =2 N , h = (b −a) = h . N 2

Тогда все узлы первой сетки будут совпадать с узлами второй сетки только с другими номерами (рис. 9.3):

xn = x2n ,

n = 0,1, , N .

Обозначим {un} и {

u

n} приближённые решения, полученные на

этих сетках, и сравним их с

точным решением задачи Коши в

совпадающих узлах. Так как

r =1 2 , асимптотическая

оценка

погрешности (6.3.7) для

{

u

2m}

примет вид

u( xm ) −

u

2m

≈

u

2m − um

Рис. 9.3

(2k −1) .

(9.1.27) Чтобы получить приближённое решение с заданной точностью ε , строится последовательность сгущающихся (в 2 раза) сеток и на

каждой из них вычисляется приближённое решение. Для каждой пары сеток, в каждом совпадающем узле xm = x2m , проверяется выполнение неравенства

u2m − um	≤ ε .	(9.1.28)
(2k −1)

Процесс построения сеток и приближённых решений на них продолжается до тех пор, пока условие (9.1.28) не будет выполняться во всех совпадающих узлах последней сетки. Последнее приближённое решение будет иметь заданную точность в этих узлах.

Поскольку погрешность приближённого решения обычно имеет наибольшее значение на правом конце отрезка [a ;b], условие (9.1.28) нередко проверяется не во всех совпадающих узлах, а только в точке

xN = x2N = b .

Многошаговые методы

Глава 9. Численные методы решения обыкновенных дифференциальных	89
уравнений

Методы Адамса

Рассмотренные вычислительные схемы Рунге – Кутта и Эйлера с алгоритмической точки зрения представляют собой циклы в которых последовательно вычисляются компоненты приближенного решения задачи Коши (9.1.1). Нулевой компонент u0 определяется до начала цикла из начального условия задачи Коши (u0 = u ), а последующие компоненты u1 , u2 , …, uN вычисляются по рекуррентной формуле. На n-м шаге цикла значение un+1 вычисляется по вычисленному на предыдущем шаге цикла значению un (значение n изменяется в цикле от 0 до N-1). Но если n достаточно велико, то будет вычислено un , un −1, un−2 , …, u0 . В этих значениях содержится дополнительная информация о точном решении задачи Коши u(x) , которую можно использовать при вычислении очередного приближенного значения un+1. Можно ожидать, что использование полученных на предыдущих шагах цикла приближенных значений (un −1, un−2 , …) приведет к повышению точности значения un+1. В этом и состоит основная идея, приведшая к появлению многошаговых вычислительных схем.

Пусть имеется вычислительная схема приближенного решения задачи Коши, в которой вычисляется un+1 по вычисленным на предыдущих шагах цикла значениям un , un −1, un−2 , …, un−p +1. Подобные вычислительные схемы получили название p-шаговых. Если p>1, то соответствующая p-шаговая схема называется многошаговой. В этой терминологии схемы Эйлера и Рунге-Кутта являются одношаговыми.

Построение многошаговых вычислительных схем сложнее, чем построение схем одношаговых. Цикл для p-шаговой вычислительной схемы начинается с n = p −1. На первом шаге цикла для вычисления значения un+1 = u p необходимо использовать значения u p −1, u p −2 , …, u0 . Они должны быть вычислены до основного цикла. При этом только значение u0 можно определить с помощью начального условия задачи Коши. Для того чтобы определить начальные компоненты приближенного решения u p −1, u p −2 , …, u1 , либо строят специальные разгонные формулы, либо используют одношаговые вычислительные схемы, например схемы Рунге-Кутта с мелким

Рис. 9.4

Глава 9. Численные методы решения обыкновенных дифференциальных	90
уравнений

шагом h0 , тем самым обеспечивая высокую точность этих начальных значений. Далее используется многошаговая вычислительная формула с крупным шагом h.

На рис. 9.4 показана сетка точек для многошаговой вычислительной схемы при p=3, h0 = h5. Крупно показаны узлы для многошаговой вычислительной формулы, а маленькими точками – узлы для одношаговой схемы, с помощью которой вычисляются начальные значения u0 , u1 , u2 .

В дальнейшем мы не будем касаться вопроса вычисления начальных компонентов при-ближенного решения

задачи Коши u p −1, u p −2 , …, u0 , а обратимся к получению формул для вычисления un+1 по вычисленным на предыдущих шагах цикла значениям un , un −1, un−2 , …, un−p +1.

Рассмотрим два семейства многошаговых вычислительных схем, получивших название схем Адамса. Схемы первого семейства обычно называют явными или схемами Адамса-Башфорта. Формула для вычисления un+1 в p-шаговых схемах Адамса-Башфорта имеет вид

un +1 =ψ (xn ,un , xn−1,un−1, , xn − p +1,un− p +1 ).	(9.1.29)
Если известны начальные значения u p −1, u p −2 , …,	u0 , то по

явной формуле (9.1.29) последовательно и без каких-либо ухищрений вычисляются остальные компоненты приближенного решения задачи Коши: u p (при n=p-1), u p +1 (при n=p), … , uN (при n=N-1). Простота использования является главным преимуществом явных схем.

Схемы второго семейства обычно называют неявными или

схемами Адамса-Моултона. Формула для вычисления	un+1 в
p-шаговых схемах Адамса-Моултона имеет вид
un+1 =η(xn+1,un+1, xn ,un , xn−1,un−1, , xn− p +1,un− p +1 ).	(9.1.30)

Неизвестная величина un+1 теперь находится и в левой, и в правой части равенства (9.1.30), причем под знаком функции η. Решить уравнение (9.1.30) аналитически можно только для отдельных частных случаев дифференциальных уравнений (9.1.1). Для того чтобы использовать неявную схему в общем случае (для произвольного дифференциального уравнения (9.1.1)) приходится использовать для решения уравнения (9.1.30) относительно un+1 итерационные численные методы, рассмотренные в главе 2. Чаще

[a,b]

Глава 9. Численные методы решения обыкновенных дифференциальных	91
уравнений

всего используется метод простой итерации. Выбирается достаточно точное начальное приближение и проводится несколько итераций. Количество итераций обычно фиксировано и невелико, иначе схема потеряет свою вычислительную эффективность.

Несмотря на все эти неудобства, неявные схемы находят применение. Дело в том, что неявные схемы оказались менее чувствительными к вычислительным погрешностям, связанным с округлениями величин в ЭВМ, нежели явные. Все явные схемы вида (9.1.29), к которым относятся и схемы Рунге-Кутта, имеют ограничения на величину шага сетки, которых не имеют схемы неявные. Поэтому при использовании неявных схем, как правило, можно работать с более крупным шагом, не боясь разболтки. А соответственно, чем крупнее шаг сетки, тем меньше вычислительные затраты и тем быстрее будет получено приближенное решение задачи Коши. Неявные схемы могут оказаться полезными в сложных случаях, когда явные схемы работают плохо.

Рассмотрим получение многошаговых формул Адамса. Напомним, что рассматривается задача отыскания приближенного сеточного решения задачи Коши (9.1.1). Точное решение задачи Коши обозначим u(x) . На отрезке введена сетка точек xn = a + n h с постоянным шагом h = (b − a)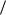 N , где n = 0,1, , N . Ищутся компоненты приближенного решения задачи Коши un (n = 0,1, , N ), которые представляют собой приближенные значения u( xn ) . Так же как при выводе формулы Эйлера, проинтегрируем обе части дифференциального уравнения (9.1.1) на отрезке [xn ; xn+1] и получим формулу (9.1.8)

xn+1	xn+1
òu′(x) dx =	ò f (x ,u( x)) dx .
xn	xn

Интеграл в левой части этого равенства найдем по формуле Ньютона-Лейбница

xn+1

òu′( x) dx = u( xn+1 ) − u( xn ) .

xn

В результате чего получим формулу, позволяющую найти значение u( xn+1 ) по известному значению u( xn ) :

u( xn+1 ) = u( xn ) + xnò+1f ( x ,u( x)) dx .

(9.1.31)

xn

Глава 9. Численные методы решения обыкновенных дифференциальных	92
уравнений
Будем считать, что точные значения u( xn ) , u( xn−1 ) , …, u( xn−k )	нам

известны, и будем искать приближенное значение u( xn+1 ) . Для этого построим интерполяционный многочлен Pk (x) по таблице значений функции ϕ( x) = f ( x,u( x)) в узлах xn , xn −1, …, xn −k

Pk ( x) = ϕ( xn ) +ϕ( xn , xn−1) ( x − xn ) +

+ϕ( xn , xn−1, xn−2 ) ( x − xn ) ( x − xn−1) + ....

+ϕ( xn , xn−1, , xn−k ) ( x - xn ) × × ( x - xn−k +1) .	(9.1.32)
Кроме того, построим интерполяционный многочлен	~	по
	Pk (x)
таблице значений функции ϕ( x) = f ( x,u( x)) в узлах xn+1, xn , …, xn−k +1
Pk ( x) =ϕ( xn+1) +ϕ( xn+1, xn ) ( x − xn+1)
+ϕ( xn+1, xn , xn−1) ( x − xn+1) ( x − xn ) +.....
+ϕ( xn+1, xn , , xn−k +1) ( x - xn+1) × × ( x - xn−k +2 ) .	(9.1.33)

Подставив в формулу (9.1.31) под знак интеграла вместо функции f ( x,u( x)) интерполяционный многочлен Pk (x), получим первое приближенное равенство для вычисления приближенного значения

u( xn+1 ) ≈ u( xn ) + xnò+1Pk ( x) dx .

(9.1.34)

xn

А подставив в формулу (9.1.31) под знак интеграла вместо функции f ( x,u( x)) интерполяционный многочлен Pk (x), получим второе приближенное равенство для вычисления приближенного значения

		xn+1~	( x) dx .	(9.1.35)
		u( xn+1 ) ≈ u( xn ) + ò Pk
		xn
Формула	(9.1.34)	порождает	семейство	формул
Адамса-Башфорта,	а формула (9.1.35)		- семейство	формул

Адамса-Моултона. Получим их для некоторых значений k. При k=0 интерполяционные многочлены

P0 ( x) = ϕ ( xn ) = f ( xn ,u( xn )) , P0 ( x) = ϕ( xn+1 ) = f ( xn+1,u( xn+1 )) ,

а формулы (9.1.34) и (9.1.35) примут вид

u( xn+1)

u( xn+1)

xn+1		( x) dx = u( xn ) + h f ( xn ,u( xn )) ,	(9.1.36)
≈ u( xn ) + ò P0
xn
xn+1~	( x) dx = u( xn ) + h f ( xn+1,u( xn+1)) .		(9.1.37)
≈ u( xn ) + ò P0

xn

Глава 9. Численные методы решения обыкновенных дифференциальных

93

уравнений

Заменив в формулах (9.1.36) и (9.1.37) точные значения u( xn )

приближенными значениями

un , а приближенные равенства

точными, получим формулу Адамса-Башфорта

(9.1.38)

un+1 = un + h f ( xn ,un )

и Адамса-Моултона

un+1 = un + h f ( xn+1,un+1) .

(9.1.39)

При k=1 интерполяционные многочлены

P1( x) = ϕ( xn ) + ϕ( xn , xn−1) ( x − xn ) =

= f ( xn ,u( xn )) +

f ( xn ,u( xn )) − f ( xn−1,u( xn−1))

( x − xn )

,

h

P1( x) = ϕ( xn+1) +ϕ( xn+1, xn ) ( x − xn+1) =

= f ( xn+1,u( xn+1)) +

f ( xn+1,u( xn+1)) − f ( xn ,u( xn ))

( x − xn+1)

P0 ( x) = ϕ( xn 1 )

h

xn 1 ))

,

= f ( xn 1,u(

+

+

+

а формулы (9.1.34), (9.1.35) принимают вид

u( xn+1) ≈ u( xn ) + xnò+1P1( x) dx =

xn

h2

= u( xn ) + h f ( xn,u( xn )) +

f ( xn ,u( xn )) − f ( xn−1,u( xn−1))

=

h

2

= u( xn ) + h [3 f ( xn ,u( xn )) − f ( xn−1,u( xn−1))],

(9.1.40)

2

xn+1~

u( xn+1) ≈ u( xn ) + òP1( x) dx =

xn

= u( xn ) + h f ( xn+1,u( xn+1)) +

f ( x

n+1

,u( x

n+1

)) - f ( x

,u( x

n

)) æ

h2 ö

n

ç

÷

ç

-

2 ÷ =

h

= u( xn ) + h [ f ( xn+1,u( xn+1 )) + f ( xn ,u( xn ))].

è

ø

(9.1.41)

2

Заменив в формулах (9.1.40), (9.1.41) точные значения u( xn )

приближенными значениями

un , а приближенные равенства

точными, получим формулу Адамса-Башфорта

un+1 = un + h [3

f ( xn ,un ) − f ( xn−1,un−1)]

(9.1.42)

2

и Адамса-Моултона

un+1 = un + h [ f ( xn+1,un+1) + f ( xn ,un )].

(9.1.43)

2

При k=2 аналогично получается формула Адамса-Башфорта

un+1	= un +	h	[23 f ( xn ,un ) −16 f ( xn−1,un−1) + 5 f ( xn−2,un−2 )]	(9.1.44)
	12

и формула Адамса-Моултона

Глава 9. Численные методы решения обыкновенных дифференциальных	94
уравнений

un+1 = un +12h [5 f ( xn+1,un+1 ) +8 f ( xn ,un ) − f ( xn−1,un−1)].

При k=3 формула Адамса-Башфорта принимаетт вид

un+1 = un + 24h [55 f ( xn ,un ) − 59 f ( xn−1,un−1) +.

+37 f ( xn−2 ,un−2 ) −9 f ( xn−3,un−3 )]

Аформула Адамса-Моултона может быть записана в виде

(9.1.45)

(9.1.46)

u

= u

+

h

[9 f ( x

,u

) +19 f ( x

,u

) −

.

(9.1.47)

24

n+1

n

n+1

n+1

n

n

− 5 f ( xn−1,un−1) + f ( xn−2 ,un−2 )]

Отметим, что

формулы Адамса

(9.1.38), (9.1.39),

(9.1.43)

являются одношаговыми. Формула (9.1.38) совпадает с соответствующей формулой в вычислительной схеме Эйлера. Формулы Адамса (9.1.42), (9.1.45) являются двухшаговыми, формулы (9.1.44) и (9.1.47) – трехшаговыми, а формула (9.1.46) – четырехшаговой.

Как известно, вычислительная схема Эйлера имеет первый порядок точности. Очевидно, порядок точности вычислительных схем, основанных на формулах Адамса, зависит от порядка k

используемых интерполяционных многочленов Pk (x)				и	Pk (x).
Конечно, он зависит и от степени гладкости функции				f (x,u) и от
порядка	точности	одношаговой	вычислительной		схемы,

используемой для вычисления значений начальных компонентов приближенного решения. Можно показать, что при выполнении соответствующих условий, вычислительные схемы, основанные на формулах Адамса (9.1.38) (9.1.39), будут иметь первый порядок точности. Вычислительные схемы, основанные на формулах Адамса (9.1.42), (9.1.43), будут иметь второй порядок точности, вычислительные схемы, основанные на формулах Адамса (9.1.44), (9.1.45), будут иметь третий порядок точности, вычислительные схемы, основанные на формулах Адамса (9.1.46) и (9.1.47), будут иметь четвертый порядок точности.

Методы прогноза и коррекции

Методы прогноза и коррекции появились как попытка соединить простоту применения явных и хорошие качества неявных вычислительных схем. Они имеют несколько разных названий, таких

Глава 9. Численные методы решения обыкновенных дифференциальных	95
уравнений

как «методы предсказания и уточнения», или «предиктор-корректорные методы». Суть этих методов состоит в совместном применении явных и неявных вычислительных схем, одинаковых или смежных порядков точности. Вначале с помощью явной схемы (9.1.29) вычисляется первое грубое приближение u~n+1, для u( xn+1 ) :

un +1 =ψ (xn ,un , xn−1,un−1, , xn − p +1,un− p +1 ).	(9.1.48)
~

А затем это грубое приближение подставляется в правую часть неявной формулы (9.1.30), и по ней находится окончательное (скорректированное) приближенное значение un+1, для u( xn+1 ) :

un+1	=η(xn+1	,un+1, xn ,un , xn−1,un−1, , xn− p +1,un− p +1 ).	(9.1.49)
		~

Такую подстановку можно интерпретировать как применение метода простой итерации для вычисления приближенного решения уравнения (9.1.30) относительно un+1. В качестве начального приближения в данном случае используется u~n+1, а по формуле (9.1.49) вычисляется первый член последовательности приближений. Для повышения точности приближения un+1 иногда применяют формулу (9.1.49) несколько раз. Например, вместо формулы (9.1.49) можно записать пару формул итерационного уточнения

ì

~

=

η (

xn+ 1

~

,xn,un,xn− 1,un− 1

, ,xn− p+ 1

,un− p+ 1

)

,

ïun+ 1

,un+ 1

(9.1.50)

í

= η (

x

~

,x

,u

,x

,u

, ,x

,u

).

ïu

n+ 1

n+ 1

,u

n+ 1

n

n

n− 1

n− 1

n− p+ 1

n− p+ 1

î

Но если делать много итераций, то количество вычислений возрастет настолько, что преимущества использования неявной схемы будут утеряны. Поэтому чаще всего ограничиваются одной или двумя итерациями.

Описанная процедура привела к созданию новых явных вычислительных схем (9.1.48), (9.1.49) или (9.1.48), (9.1.50). Подобные вычислительные схемы получили название схем прогноза и коррекции.

Остановимся подробнее на схемах прогноза и коррекции, базирующихся на формулах Адамса-Башфорта, и Адамса-Моултона одинаковых порядков точности. Обозначим через unА+1 начальное приближение, получаемое по явной формуле Адамса-Башфорта и запишем предикторно-корректорные вычислительные формулы Адамса различных порядков точности.

Глава 9. Численные методы решения обыкновенных дифференциальных	96
уравнений

Формулы первого порядка точности

unА+1 = un + h f ( xn ,un ) ,

1).

(9.1.51)

un 1 = un + h f

(xn 1,unА

(9.1.52)

+

+ +

Формулы второго порядка точности

unА+1 = un + h [

3 f ( xn ,un ) − f ( xn−1,un−1)]

(9.1.53)

2

un+1 = un + h

[f (xn+1,unА+1)+ f ( xn ,un )].

(9.1.54)

2

Формулы третьего порядка точности

unА+1

= un

+

h

[23 f ( xn ,un ) −16 f ( xn−1,un−1) + 5 f ( xn−2 ,un−2 )]

,

(9.1.55)

12

un+1

= un

+

h

[5 f (xn+1,unА+1)+ 8 f ( xn ,un )

− f ( xn−1,un−1)].

(9.1.56)

12

Формулы четвертого порядка точности

u А

= u

+

h

[55 f ( x

,u

) −59 f ( x

,u

) +

.

(9.1.57)

24

n+1

n

n

n

n−1

n−1

+ 37 f ( xn−2 ,un−2 ) −9 f ( xn−3,un−3 )]

u

= u

+

h

[9 f (x

,uБ

)

+19 f ( x

,u

) −

.

(9.1.58)

n+1

n

24

n

+1

n+1

n

n

−5 f ( xn−1,un−1) + f ( xn−2 ,un−2 )]

Обычно

многошаговые

предикторно-корректорные

вычислительные

схемы

Адамса

имеют

более

высокую

вычислительную эффективность (требуется производить меньше вычислений для получения результатов с заданной точностью), чем одношаговые вычислительные схемы Рунге-Кутта такого же порядка точности. Чаще всего на практике используют четырехшаговую предиктор-корректорную вычислительную схему Адамса, основанную на формулах (9.1.57), (9.1.58).

9.2. Решение задач Коши для обыкновенных дифференциальных уравнений высших порядков и систем

Задачи Коши для уравнения m-го порядка и для системы уравнений

Рассмотрим задачу Коши для обыкновенного дифференциального уравнения m–го порядка. Она формулируется следующим образом. Требуется определить функцию u(x) ,

Глава 9. Численные методы решения обыкновенных дифференциальных уравнений

имеющую производную m–го порядка на отрезке удовлетворяющую дифференциальному уравнению

u (m) = f (x ,u ,u′,u′′, ,u(m−1) ), x [a ;b]

и начальным условиям

ìu(a) = u1 ,
ïïu¢(a) = u2 ,
í...............
ï	(m−1)
ï		(a) =	um .
îu

97

[a ;b], (9.2.1)

(9.2.2)

Здесь f − заданная функция m+1 переменной, a ,b ,u1 ,u2 , ,um −

заданные постоянные.

Путём замены переменных эта задача сводится к задаче Коши для системы из m дифференциальных уравнений первого порядка. Введём m новых функций:

u1( x) = u( x),u2 ( x) = u′( x) , ,um ( x) = u(m−1) ( x) . Если функция u(x) является решением задачи Коши (9.2.1) − (9.2.2), то введенные функции будут,

очевидно, удовлетворять задаче Коши

ìu1′		= u2 ,
ï	¢	= u3 ,
ïu2
ï									x [a ;b] ,
í...............
ï	¢
ïum−1 = um ,							, ,u		)
ïu¢		= f ( x,u ,u				2		m
î	m	1
ìu1(	a) =		u1 ,
ïïu2 (a) =				u	2 ,

í...............

ï

ïîum (a) = um .

(9.2.3)

(9.2.4)

По этой причине мы не будем далее отдельно рассматривать задачу (9.2.1) − (9.2.2), а сразу рассмотрим более общую задачу

Коши для системы из m дифференциальных уравнений первого порядка. Она сформулирована следующим образом. Требуется определить функции u1( x),u2 ( x), ,um ( x) , дифференцируемые на отрезке [a ;b], удовлетворяющие системе дифференциальных уравнений