Вишка. Клочко

	x	y +1	z −1		=0; –12x+6(y+1)–12(z–1)=0; 2x–(y+1)+2(z–1)=0; 2x–y+2z–3=0.
	3	6	0
	1	− 2	− 2

Зведемо це рівняння площини до нормального вигляду. Оскільки її нормальним вектором є вектор N=(2;–1; 2), то N =3. Поділивши рівняння

на 3, дістанемо	2x − y + 2z − 3	= 0. Тоді шукана відстань d від точки S до
	3			2·1− 4 + 2·(−2) − 3			9
цієї площини	буде такою:	d=				=		=3. Отже, висота
				3			3

піраміди h дорівнює 3.

Відповідь: 3.

3.4 Пряма в просторі 3.4.1 Канонічні рівняння прямої

Положення прямої відносно декартової системи координат Оxyz повністю визначається точкою М 0 ( x0; y0; z0 ), що лежить на ній і вектором

s, який паралельний цій прямій або лежить на ній. Нехай s =(m, n, p), де m, n і p – задані числа. Вектор s, паралельний даній прямій, називається

напрямним вектором прямої.

							Нехай М (x; y; z) – біжуча точка прямої.
					Розглянемо вектор
					М 0 М =( x – x0 ; y – y0 ; z					− z0 ), який лежить на
					самій прямій і своїм рухомим кінцем вирисовує
					саму		пряму. Оскільки			вектори М 0 М і s
					колінеарні, то їх координати пропорційні. Отже,
					маємо
	x − x0	=		y	− y0	=		z − z0	.	(3.22)
	m				п			р

Рівняння (3.22) називається канонічними рівняннями прямої в просторі.

Звернемо увагу на те, що ці рівняння узагальнюють відповідне канонічне рівняння прямої на площині, яке мало аналогічний вигляд, але містило дві біжучі координати точки, і співвідношення (3.22) розглядається як

система двох лінійних рівнянь з трьома змінними.

Приклад 14. Скласти рівняння прямої, що проходить через дві дані точки М1 (2;–1;3) і М 2 (3;–1;–1).

Розв’язування. Вектор М1 М 2 =(1;0;–4), що лежить на даній прямій, є її напрямним вектором. Нехай М (x;y;z) – біжуча точка прямої. Достатньо

розглянути один із двох векторів М1 М або М 2 М із рухомим кінцем,

60

наприклад,				вектор			М1 М =(x–2; y+1; z–3). Оскільки вектори М1 М і
M1M2		колінеарні, то їх координати пропорційні, тобто
	x - 2	=	y	+1	=	z - 3		. Це і є канонічні рівняння прямої. Незважаючи на
1			0				4

некоректність другого відношення, такий запис вважається зручним. Цей запис виражає лише особливість даної прямої, а саме: ця пряма перпендикулярна до осі Оy, бо ординати точок М1 і М 2 збігались і y = –1 є сталою, тому ця пряма перпендикулярна до осі Оy.

3.4.2 Векторне рівняння і параметричні рівняння прямої

Нехай вектор s = (m,n, p)−напрямний вектор прямої, яка проходить

через дану точку М 0 (x0 , y0 , z0 ). Якщо				M (x, y, z)− біжуча точка прямої, то
вектор М 0 М -	вектор	з рухомим кінцем			буде мати	змінну	довжину.
Враховуючи це і те, що вектори			М 0 М	і s	колінеарні,	за теоремою про
колінеарні вектори будемо мати,			що М 0 М = t ×s, де t змінний скалярний
множник. Якщо провести радіуси-вектори точок М0 і М,						а саме: r0		= OM0 ,
а r = OM , то вектор M 0 M є різницею векторів r і r0 ,						тобто M 0 M = r− r0 .
Тоді рівняння M0M = ts запишеться так:
		r − r0 = t s,						(3.23)
де t – змінна скалярна величина, t R .
Рівняння (3.23) називається векторним рівнянням прямої.
Оскільки	вектор	М0М = r- r0 =( x − x0 ; y − y0 ; z − z0 ),					а	вектор

t × s = (tn;tm ;tp ), то в рівних векторів рівні декартові координати. Отже,

будемо мати, що

ìx - x0 = tm,

ïíy - y0 = tn, або

ïîz - z0 = tp

ìx = tm + x0 ,
ï	(3.24)
íy = tn + y0 ,
ï	де t Î R.
îz = tp + z0 ,

Рівності (3.24) називаються параметричними рівняннями прямої,

змінна t називається параметром. Звернемо увагу на те, що змінні декартові координати біжучої точки прямої є лінійними функціями незалежної змінної t, яка є параметром.

Перехід від канонічних рівнянь прямої (3.22) до параметричних рівнянь (3.24) можна здійснити дуже простим прийомом; а саме: змінне спільне відношення позначити буквою t – змінна величина, і виразити x, y

і z через змінну t. Навпаки, щоб від параметричних рівнянь (3.24) перейти до канонічних рівнянь, треба з кожного з рівнянь системи (3.24)

61

	виключити параметр t, а саме:t =	x − x0	,	t =	y − y0	і t =	z − z0	, і звідси
		m			n		p

видно, що ці відношення рівні, тобто випливає відповідна пропорційність. Таким чином, канонічні і параметричні рівняння прямої є

рівносильними.

3.4.3 Загальні рівняння прямої

Пряму в просторі можна розглядати як лінію перетину двох площин. Якщо ці площини, що перетинаються, задати їх загальними рівняннями, а саме: A1x + B1 y + C1z + D1 = 0 і A2 x + B2 y + C2 z + D2 = 0 , то координати біжучої точки прямої, по якій ці площини перетинаються, повинні задовольнити кожне із цих рівнянь, тобто задовольнити систему цих рівнянь.

Таким чином, пряма в просторі описується системою двох рівнянь

першого степеня з трьома змінними, а саме:
ìA x + B y + C z + D = 0,				(3.25)
í 1	1	1	1
îA2 x + B2 y + C2 z + D2 = 0.

З геометричної точки зору видно, що дану пряму можна тлумачити як перетин деякої пари площин, що входять в пучок площин, що проходять по даній прямій, яких є безліч.

Обернено, всяка сумісна система вигляду (3.25) визначає в просторі деяку певну пряму, оскільки кожне із рівнянь визначає деяку площину і ці дві площини, якщо вони не є паралельними, перетинаються по цілком певній прямій. Таким чином, система (3.25) сумісних рівнянь визначає деяку пряму в просторі. Рівняння (3.25) називаються загальними

рівняннями прямої.

Недолік цього способу задання прямої в просторі полягає в тому, що нам важко визначити орієнтацію прямої відносно системи координат. Тому часто доводиться від загальних рівнянь прямої переходити до її канонічних рівнянь, які більш зручно характеризують саму пряму. Але для цього треба на прямій, що визначається рівняннями (3.25), вказати деяку точку М0 і її напрямний вектор. Як це зробити, виходячи із загальних рівнянь прямої?

Точку М0, що лежить на прямій, знайти досить просто, якщо врахувати, що на прямій є безліч точок. Досить замість z (або замість однієї з двох інших біжучих координат х і у) підставити довільно вибране значення z0, якщо пряма не паралельна площині х0у, і відносно двох інших змінних координат х і у із даної системи (3.25) скласти систему двох рівнянь з двома змінними х і у. Розв’язавши одержану систему, знайдемо абсцису і ординату шуканої точки М0 з аплікатою z = z0 .

Напрямний вектор s прямої можна визначити, якщо врахувати, що цей вектор паралельний прямій або лежить на ній. Оскільки за кожним із

62

рівнянь, що входять в склад системи (3.25), можна визначити нормальні вектори N1 =( А1 , В1 ,С1 ) і N2 = (A2 , B2 ,C2 ) площин, що, перетинаючись,

утворюють пряму і ці вектори перпендикулярні до цих площин, то вектори N1 і N2 перпендикулярні самій прямій, а значить, і вектору s. Отже, вектор s повинен бути перпендикулярним до двох відомих векторів N1 і N2, а таким вектором за означенням є вектор, що дорівнює векторному добутку

векторів N1 і N2.	s =N1×N2 .
Таким чином,

Приклад 15. Звести до канонічного вигляду рівняння прямої

ìx − 2y + 3z − 4 = 0,

íî3x + 2y - 5z - 4 = 0.

Розв’язування. Знайдемо певну точку М0 на цій прямій. Нехай z = 0 ,

ìx − 2y = 4,

тоді дістанемо систему рівнянь í

î3x + 2y = 4.

Додавши почленно ці рівняння, матимемо 4x = 8 , звідки x = 2, тоді y = −1. Отже, точка М0 (2 ;−1; 0)− конкретна точка, що лежить на цій прямій.

Знайдемо напрямний вектор s прямої. За даними загальними рівняннями площин знайдемо їх нормальні вектори, а саме: N1 = (1; − 2 ; 3) і

N2 = (3; 2 ; − 5). Користуючись формулою

s =N1×N2,

будемо мати

s = N1´ N2 =

i

j

k

= 4i+14 j+ 8k . Отже, s= (4 ;14 ;8).

1

- 2

3

3

2

- 5

Нехай М (x, y, z) – біжуча точка прямої. Оскільки вектор

M 0 M = (x − 2; y +1; z)

колінеарний

з вектором

s = (4 ;14 ;8),

то

їх

координати пропорційні, тобто

x − 2

=

y +1

=

z

або

z − 2

=

y +1

=

z

.

2

x − 2

y +1

4

14

8

7

4

Відповідь:

=

=

z

.

2

7

4

3.4.4 Кут між прямими

Нехай дві прямі задані канонічними рівняннями, а саме:

x − x1

=

y − y1

=

z − z1

і

x − x2

=

y − y2

=

z − z2

,

m

n

p

m

2

n

2

p

2

1

1

1

де s1 = (m1 ,n1 , p1 ) і s2 = (m2 ,n2 , p2 ) ― їх напрямні вектори.

Кут ϕ між цими мимобіжними прямими дорівнює куту між векторами s1 і s2 як кути із взаємно паралельними сторонами. Тоді матимемо, що

cosϕ =

s1× s2

або cosϕ =

m1m2 + n1n2 + p1 p2

. (3.26)

s1

×

s2

m2

+ n2

+ p2

× m2

+n2

+ p2

1

1

1

2

2

2

63

Дві прямі паралельні тоді і тільки тоді, коли

m1

=

n1

=

p1

.

(3.27)

m2

n2

p2

Дві прямі перпендикулярні тоді і тільки тоді, коли

m1m2 + n1n2 + p1 p2

= 0 .

(3.28)

Приклад 16. Переконатись, що прямі перпендикулярні, якщо

ì2х + у - 4z + 2 = 0,

ìx = 1+ 2t,

і

ï

í

= 0

íy = -2 + 3t,

î4x - y - 5z + 4

ï

- 6t.

îz = 1

Розв’язування. Знайдемо напрямні вектори цих прямих. Користуючись загальними рівняннями прямої, знайдемо її напрямний вектор:

s1 =N1×N2, де N1 = (2 ;1;- 4), N2 = (4 ;−1;- 5), тоді

s1 =	i	j	k	= -9i - 6 j - 6k , тобто s1 = (- 9 ; − 6 ; - 6).
	2	1	- 4
	4	-1	- 5

Із параметричних рівнянь другої прямої знаходимо, що s2 = (2 ;3; - 6). Оскільки s1× s2 = 18 -18 + 36 = 0, тоді маємо, що вектори s1 і s2 –

перпендикулярні, тоді і прямі перпендикулярні.

Приклад 17. Задані вершини трикутника А(3 ; 6 ;− 7 ), В( − 5; 2 ; 3) і С(4; –7; –2). Скласти параметричні рівняння його медіани, проведеної

з вершини С.

Розв’язування. Знайдемо спочатку координати точки D – середини

сторони АВ: xD =	3 − 5	= -1;	yD =	6 +	2	= 4 ;	zD =	− 7 + 3	= -2 . Отже,
	2			2				2
D(-1;4 ; - 2).

На медіані СD виберемо біжучу точку M (x, у, z) і розглянемо вектори

CM і CD , які є колінеарними, причому вектор CD є напрямленим вектором медіани. За теоремою про колінеарні вектори матимемо:

СМ = t ×CD . Знайдемо координати цих векторів: СМ = (х - 4 ; у + 7 ; z + 2),

CD = (- 5;11;0) і t ×CD = (- 5t ;11t ;0).	З рівності	векторів СМ і t ×CD
випливає рівність їх координат. Отже,	x − 4 = −5t ;	y + 7 = 11t ; z + 2 = 0 ,

звідки x = −5t + 4; y = 11t − 7 ; z = −2 .

Відповідь: x = −5t + 4; y = 11t − 7 ; z = −2 .

3.4.5 Відстань від точки до прямої

х − х0

y − y

z − z0

Нехай

задано

точку

M1 (х1,

у1,

z1)

і пряму

=

=

.

m

n

M1

P

Знайдемо

відстань

від

точки

до

прямої,

якою

буде

довжина

перпендикуляра, опущеного із цієї точки на цю пряму. З канонічних рівнянь прямої визначаємо її нормальний вектор s = (m, n, p) і точку

64

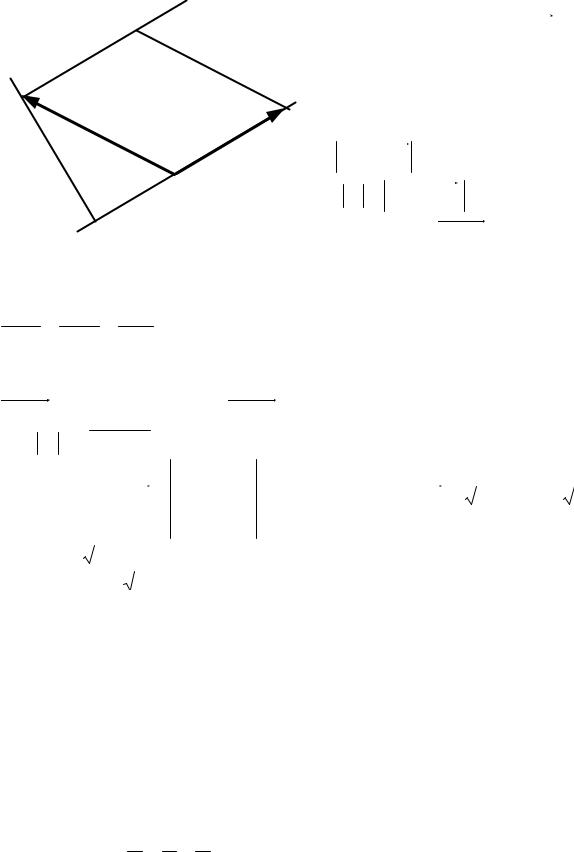
M 1

s

M 0

M 2 Рисунок 3.11

M 0 (x0 , y0 , z0 ). Побудуємо паралелограм на векторах s і М 0 М1 як на сторонах, що виходять із точки M 0 (рис. 3.11). Площа цього

паралелограма, з					одного	боку,
дорівнює d ×		s		,	а з	іншого

s × M0M1 . Отже, маємо рівність d × s = s × M0M1 , звідки дістане-

мо, що d =	s × M		0M1		.	(3.29)
		s

Приклад 18. Знайти відстань від точки М1 (1;–1; 2) до прямої x −2 2 = y +2 2 = z−−11.

Розв’язування. З канонічних рівнянь прямої визначаємо її напрямний вектор s = (2;2 ;− 1) і точку М0 (2;–2; 1). Знайдемо координати вектора

М 0М1 і довжину вектора s: М 0М1 = (− 1;1;1) і

s= 4 + 4 +1 = 3.

ij k

Оскільки s × M0M1 = 2

2

−1 = 3i− j+ 4k ;

s × M0M1

=

9 +1+16

=

26

.

Отже, d =

/3.

−1

1

1

26

Відповідь:

/3.

26

3.5 Пряма і площина

3.5.1 Кут між прямою і площиною

Нехай задана площина

загальним рівнянням Ax + By + Cz + D = 0 і

пряма канонічними рівняннями

x − x0

=

y − y0

=

z − z0

.

m

n

p

Оскільки

нормальний

вектор

площини

N = (A;B;C) перпендику-

лярний до площини, а напрямний вектор прямої s = (m,n, p) паралельний прямій, то умова перпендикулярності прямої до площини полягає в тому,

що N || s, тобто mA = Bn = Cp .

Пряма паралельна площині, якщо N s, тобто коли

Am + Bn + Cp = 0.

65

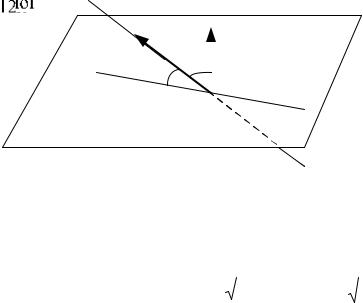
Кутом між прямою і площиною називається один із суміжних кутів ϕ або π − ϕ , утворених даною прямою і її проекцією на цю площину.

Позначимо кут між прямою і

площиною через ϕ , а кут між

φ

α

нормальним вектором

N

і

напрямним

вектором

s

–

через α (Рис. 3.12).

Оскільки

кути ϕ

і

α

є

доповняльними, а кут α

можна

визначити

за

формулою cos α =

N× s

,

то

N

×

s

враховуючи

sinϕ =			N× s
			N		×		s

те, що		cosα = cos(π / 2 − ϕ)= sinϕ ,					матимемо, що
або sinϕ =		Am + Bn + Cp
						.	(3.30)
			×
		A2 + B2 + C 2		m2 + n2 + p2

3.5.2 Точка перетину прямої з площиною

Нехай площину і пряму задано відповідно загальним рівнянням і канонічними рівняннями

Ax + By + Cz + D = 0 і	x − x0	=	y − y0	=	z − z0	.
	m		n
					p

Якщо пряма не є паралельною площині, то вони перетинаються тільки в одній точці. Як знайти їх точку перетину?

Оскільки точка перетину прямої з площиною є їх спільною точкою, то її координати повинні задовольнити і рівняння площини, і рівняння прямої, тобто координати їх точки перетину є розв’язком системи, складеної з цих рівнянь, а саме:

	ìAx + By + Cz + D = 0,
	ï			y - y0		z - z0
	í x - x0		=		=		.
	ï	m		n		p
	î

Це є система трьох лінійних рівнянь з трьома невідомими x, y і z .

Як її розв’язати? Можна скористуватись будь-яким із відомих способів. Але зручно цю систему розв’язати так.

Від канонічних рівнянь прямої переходять до її параметричних рівнянь: x = mt + x0 , y = nt + y0 , z = pt + z0.

Підставляють ці лінійні вирази в загальне рівняння площини Ax + By + Cz + D = 0 , в результаті чого дістаємо лінійне рівняння відносно

однієї змінної t . Розв’язавши це рівняння, дістанемо значення параметра t , яке відповідає точці перетину. Якщо це рівняння має єдиний розв’язок, то за цим знайденим значенням змінної t знайдемо координати точки перетину.

66

Якщо ж це лінійне рівняння має безліч розв’язків, то буде безліч спільних точок прямої з площиною, тому дана пряма лежить в даній площині.

Якщо ж це лінійне рівняння не має розв’язків, то це означатиме, що пряма паралельна площині, що можна виявити безпосередньо за

кординатами нормального вектора N і напрямного вектора s.

Приклад 19. Знайти точку

перетину

прямої

x − 5

=

y − 2

=

z + 1

з

2

-1

площиною 2x − y + 3z + 9 = 0.

3

Розв’язування. Координати

шуканої

точки

повинні

задовольнити

ì x - 5

=

y - 2

=

z +1

ï

2

-1

3 .

систему рівнянь í

ï

î3x - y + 3z + 9 = 0.

Перейдемо від канонічних рівнянь прямої до параметричних рівнянь, прирівнявши кожне із відношень до параметра t , дістанемо: x = 2t + 5, 3 y = −t + 2, z = 3t −1. Підставивши ці вирази в рівняння 3x − y + 3z + 9 = 0,

матимемо:

2(2t + 5)− (− t + 2)+ 3(3t −1)+ 9 = 0; 14t + 14 = 0, звідки t = −1.

Отже, значенню параметра t , що дорівнює − 1, відповідає спільна точка прямої і площини. Підставимо це значення в параметричні рівняння, дістанемо: x = 3, y = 3, z = −4.

Отже, точка M 0 (3;3;− 4)− точка перетину прямої з даною площиною.

Відповідь: (3;3;− 4).

Приклад 20. Знайти проекцію точки A(1;3;− 4) на площину

3x + y − 2z = 0.

Розв’язування. Проекцією точки на площину є основа перпендикуляра, опущеного із точки на цю площину, або точка перетину з площиною прямої, що проходить через точку А перпендикулярно до цієї площини. Складемо рівняння такої прямої, для чого на цій прямій виберемо біжучу

точку М (x, y, z) і розглянемо вектор AM = (x -1; y - 3; z + 4). З нормальним вектором площини 3x + y − 2z = 0, яким є вектор N=(3;1;–2), вектор AM

колінеарний							(чому?), тому їх		координати	пропорційні, тобто
	x −1		=	y − 3		=	z + 4	.
	3						- 2
			1
	Знайдемо						тепер точку перетину		цієї прямої	з даною площиною,

розв’язавши систему їх рівнянь. Від канонічних рівнянь прямої перейдемо до параметричних рівнянь за відомим нам уже з попереднього прикладу прийомом, будемо мати: x = 3t + 1, y = t + 3 і z = −2t − 4.

Підставимо ці вирази в дане рівняння площини:

3(3t + 1)+ (t + 3)− 2(− 2t − 4)= 0; 14t + 14 = 0; t = −1. При t = −1 маємо

67

x = −3 + 1= −2; y = −1+ 3 = 2; z = 2 − 4 = −2. Отже, шуканою проекцією є

точка В(–2; 2;–2) Відповідь: (–2; 2;–2).

Приклад 21. Знайти проекцію точки А(2;–1; 3) на пряму

3x = y +5 7 = z −2 2.

Розв’язування. Шукану проекцію можна розглядати як точку перетину даної прямої з площиною, що проходить через точку А перпендикулярно до даної прямої. Зауважимо, що напрямний вектор прямої s = (3; 5; 2) буде нормальним вектором цієї площини.

Нехай M (x, y, z)- біжуча	точка площини. Розглянемо вектор
AM = (x - 2; y + 1; z - 3), який	буде перпендикулярний до вектора s,

дістанемо рівняння 3x + 5y + 2z − 7 = 0. Це і є рівняння вказаної площини.

Точку перетину даної прямої з цією площиною знайдемо, розв’язавши систему рівнянь, складену з канонічних рівнянь даної прямої і рівняння цієї площини. Перейдемо від канонічних рівнянь прямої до її параметричних рівнянь, матимемо: x = 3t, y = 5t − 7, z = 2t + 2. Підставимо

ці		вирази			в рівняння площини, дістанемо: 3×3t + 5(5t - 7)+ 2(2t + 2)-
− 7 = 0, 38t − 38 = 0,							звідки	t =1 − значення параметра, що відповідає їх
спільній точці. При t =1								маємо: x = 3, y = 5 − 7 = −2, z = 2 + 2 = 4. Отже,
шуканою проекцією буде точка В(3;–2; 4).
		Відповідь: (3;–2; 4).
		Приклад 22. Скласти рівняння площини, що проходить через пряму
	x −1		=	y + 2	=	z − 2	перпендикулярно до площини 3x + 2y − z − 5 = 0.
2		- 3			2
		Розв’язування.					З канонічних рівнянь прямої визначимо її напрямний

вектор s = (2;–3; 2) і точку М0(1;–2; 2), що лежить на даній прямій. Нехай M (x, y, z)- біжуча точка площини. Розглянемо, вектор

M 0M = (x -1; y + 2; z - 2), який повністю лежить в цій площині. Оскільки

ця площина перпендикулярна до даної			площини		3x + 2y − z − 5 = 0,
нормальний вектор якої N = (3; 2;–1),			то вектори				M 0 M ,s і N –
компланарні, тому (M0M ´ s)× N = 0 або		x -1 y + 2		z - 2
		2	- 3	2			= 0;
		3	2	-1

- (x -1)+ 8(y + 2)+ 13(z - 2)= 0; звідки маємо x − 8y − 13z + 9 = 0.

Відповідь: x − 8y − 13z + 9 = 0.

3.6 Криві другого порядку

Важливим є випадок, коли лінія в декартовій системі координат 0ху описується рівнянням другого степеня з двома змінними, яке в загальному

68

вигляді можна записати так:

Ax2 + 2Bxy + Cy2 + Dx + Ey + F = 0,

де А, В, С, D, E, F – задані числа, а х і у – змінні.

Такі лінії називаються кривими другого порядку. До них відносяться коло, еліпс, гіпербола і парабола.

3.6.1 Рівняння кола

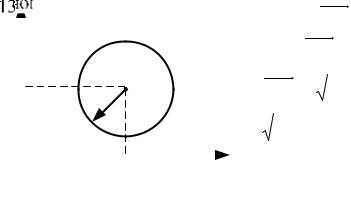
Складемо рівняння кола з центром в деякій точці С(а;b) і радіусом R.

Нагадаємо, що колом називається множина всіх точок площини, рівновіддалених від даної точки, що називається центром кола. Виберемо на колі біжучу точку М(х; у). Розглянемо

вектор CM = (x − a; y − b). За означенням

кола

CM

= R. Оскільки

=

, то матимемо

CM

(x − a)2 + (y − b)2

= R ,

(x − a)2 + (y − b)2

звідки

(x − a)2 + (y − b)2 = R2.

(3.31)

Це і є шукане рівняння кола.

Зокрема,

якщо

центр

кола

знаходиться в початку координат, то його рівняння має вигляд

x2 + y2 = R2 ,

(3.32)

саме це рівняння вивчалось в шкільному курсі.

Звернемо увагу на те, що, якщо в рівнянні (3.31) розкрити дужки, то дістанемо рівняння x2 + y2 − 2ax − 2by + a2 + b2 − R2 = 0. Звідси видно, що

старші коефіцієнти (коефіцієнти при других степенях змінних) рівні між собою, відсутній член з добутком змінних координат. Це є ознакою, що рівняння 2-го степеня з двома змінними описує коло.

3.6.2 Еліпс

Означення. Еліпсом називається множина точок площини, сума відстаней яких від двох даних точок цієї самої площини, що називаються фокусами еліпса, є величиною сталою і більшою, ніж відстань між фокусами.

Складемо рівняння еліпса. Нехай на площині задано дві точки F1 і F2 ,

які називаються фокусами еліпса. З метою одержати найбільш простий вигляд рівняння еліпса систему координат розмістимо так, щоб вісь Ox проходила через ці задані точки, а вісь Oy ділила відрізок між ними

навпіл. З механічної точки зору, лінію, що ми називаємо еліпсом, можна вирисувати так: між фокусами, закріпити гвіздками її кінці в фокусах, натягнути нитку гострим кінцем олівця і описати рухом олівця при

69