1.Метод координат на прямой

2.Простое отношение трёх точек на оси.

3.Прямоугольные декартовы координаты на плоскости.

4.Полярная система координат на плоскости.

5.Прямоугольные декартовые координаты пространств.

6.Уравнение линии как геометрического места точек на плоскости. Общее уравнение прямой. другие виды уравнения прямой на плоскости (уравнение прямой с угловым коэффициентом; уравнение прямой с данным угловым коэффициентом и проходящей через данную точку; уравнение прямой, проходящей через две данные точки; уравнение прямой в «отрезках»).

7.Нету

8.Нету

9.Угол между двумя прямыми. Расстояние от точки до прямой.

10.Линии второго порядка. Окружность.

11.Линии второго порядка.Эллипс

12. Линии второго порядка.Гипербола.

13. Линии второго порядка. Парабола

14. Основные понятия и определения. Теория матрицы.

15. Линейные действия над матрицами

16.Произведение матриц

17.Транспонировние матрицы

18. Определители 2-ого и 3-ого порядков.

19. Обратная матрица

20. Ранг матрицы

21. Система линейных уравнений. Основные понятия

22. Решение систем линейных уравнений с помощью определителя(теорема Крамера)

23. Исследование систем линейных уравнений (теорема Кронекера-Капелли, базисный минор, базисные и свободные неизвестные)

24.МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

25. Метод Гаусса решения систем линейных уравнений.

26.Комплексные числа .Понятие КЧ. Арифметические действия над КЧ.Модуль и аргумент КЧ--НЕТУ-

27.Вектор.Основные понятия.

28. Линейными операциями над векторами

29.Умножение вектора на число. Свойства линейных операций над векторами.

30.Угол между векторами. Скалярное произведение векторов.

31.Составляющие вектора: на плоскости, по прямой и плоскости, по трем прямым.

32. Разложение вектора по базису

33.Прямоугольные декартовы координаты в пространстве.

34. Длина вектора. Линейные операции над векторами в прямоугольных координатах: сумма, разность, умножение на число. Признак коллинеарности двух векторов в прямоугольных координатах.

35. Скалярное произведение векторов

36. Векторным произведением векторов

37. Смешанное произведение 3 векторов.

38. Линейная зависимость векторов

39. Уравнение поверхности и линии

40. Различные виды уравнения плоскости (частные виды уравнения плоскости; Уравнение плоскости, проходящей через данную точку перпендикулярно нормальному вектору; уравнение плоскости в отрезках; уравнение плоскости, проходящей через три данные точки; Уравнение плоскости, проходящей через две данные точки и параллельные данному вектору; Уравнение плоскости, проходящей через данную точку и параллельной двум неколлинеарным векторам)

41. Прямая в пространстве (направляющий вектор, каноническое уравнение) .Параметрическое уравнение прямой. Уравнение прямой, проходящей через две данные точки

42.-НЕТУ- числовые множества. Отрезок, интервал, промежуток.

43.Постоянные и переменные величины.Функциональная зависимость.Понятие функции и основные способы ее задания.

44.Понятие сложной функции. Четные и нечетные функции, переодические функции.Основные элементарные функции.

45. Функция натурального аргументы и ее предел.

46. БМиББ последовательность.

47. Предел функции в точке и на бескон. Определение.

48. БМ и ББ фу-ции . Определение и основные свойства.

49. Основные св-ва пределов функций.

50. Замечательные пределы

51.Непрерывные ф-ции.Точки разрыва ,их классификация

1. Метод координат на прямой

На всякой прямой можно выделить два направления: положительное и отрицательное.

Прямую, на которой указано положительно направление наз. осью. Отрезок, ограниченный точками М1 и М2 называется направленным отрезком, если указана какая и з точек М1 и М2 является началом, а какая концом. Направленный отрезок как и любой другой имеет длинну. Длинну направленного отрезка М1М2 (с чертой) обозначим |М1М2|(с чертой). Направленный отрезок расположенный на оси имеет ещё одну характеристику – величину. Величиной направленного М1М2(с чертой) некоторой оси называют его длинну |М1М2|(с чертой), взятую со знаком + если направление МО совпадает с направлением оси и знаком – в противном случае. Величина направленного отрезка М1М2 обозначается просто М1М2. Справедливы равенства |М1М2| (с четой) = |М2М1| = |М1М2|, М1М2 = -М2М1

Координатной прямой назовём ось на которой зафиксировано начало отчёта О и выбран масштаб для изменения длин. Ох – обозначение. Координатой М координатной прямой Ох назовём величину ОМ направленного отрезка ОМ (с чертой). Мх обозначение. Расстояние между точками М1х1 и М2х2 вычисляется по формуле: ϸ(М1М2) = |М1М2|=|х2-х1|. А величину формулой: М1М2=х2-х1.

2. Простое отношение трёх точек на оси.

Пусть точки М1, М2, М лежат на одной оси причём М2 не совпадает ни с М1, ни с М. Простым отношение трёх точек М1, М2, М взятых в указанном порядке, называется число (ʎ).

ʎ=(М1М2М)=М1М/ММ2.

Если М лежит внутри вне отрезка М1М2, то говорят, что М делит отрезок М1М2 внутренним (внешним) образом, при этом: ʎ>0(ʎ<0).

Если ʎ=1, то М – середина М1М2. Пусть М1(х1), М2(х2), М(х) – точки координатной прямой Ох причём х2 не равно х1; х2 не равно х, тогда ʎ=(х-х1)/(х2-х), откуда х=(х1+ʎх2)/(1+ʎ). Если М –середина отрезка (ʎ=1), то х=(х1+х2)/2.

3. Прямоугольные декартовы координаты на плоскости.

Прямоугольные декартовы системы координаты на плоскости определяются заданием масштаба и двух взаимно перпендикулярных осей, занумерованных в определённом масштабе. О – начало координат, Ох-ось абсцисс, Оу –ось ординат, Оху – обозначение.

Прямоугольные декартовы координат М – числа, определяемые равенствами: х=ОМх, у=ОМ, где ОМх(с чертой), Ому(с чертой) – величины направленных отрывков. Соответственно осей Ох, Оу. Пишут М (х,у). О(0,0) – начало координат имеют нулевые координаты.

Расстояние между М1(х1у1) и М2(х2у2) определяется по формуле: ϸ(М1М2)=корень квадратный из (х2-х1)в квадрате + (у2-у1)в квадрате. В частности, расстояние М(х,у) от начала координат О(0,0). ϸ(ОМ) Оху, тогда М(х,у) делящие направленный отрезок М1М2 (с чертой) в отношении ʎ не равно -1 определяются формулами:

Х=(х1+ ʎх2)/(1+ ʎ), у = (у1+ ʎу2)/(1+ ʎ).

В частности если М – середина М1М2, то х=(х1+х2)/2, у=(у1+у2)/2

Если М1(х1у1), М2(х2у2), М3(х3у3) – три точки, не лежащие на одной прямой, то площадь треугольника М1М2М3 вычисляется по формуле: S = +-1/2[(х2-х1)*(у3-у1)-(х3-х1)*(у2-у1)]

Причём знак +, когда выражение в квадратных скобках > 0, а знак – когда < 0.

4. Полярная система координат на плоскости.

На ряду в прямоуг. декартовой системе координат на плоскисти может быть введена полярная система координат.

ρ М(ρ,)

0 1 А

Для этого зафиксируем на плоскости какую-л. т. О кот. назовем полюсом, проведем луч ОА наз. полярной осью, выберем масштаб для измерения длин и оговариваем полож. направл. поворота вокруг О(против часовой стрелки). При таком подходе положение любой т. М на плоскости может быть определено на основе характеристик: – расстояние от т. М до полюса О;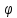– угол поворота луча ОА до совпадения с лучом ОМ. Для того чтобы каждая т. плоскости получила вполне определенные значения ρ и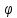достаточно считать:

– π <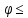π (1)

а в полюсе – =0

Для всех т. плоскости ρ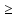0,как расстояние. Величина ρ и наз. полярными координатами т. М (ρ-[полярный радиус],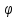- [поляр.углом]). Значение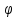связанные двойным неравенством один наз. главным знач. полярного угла.

у М

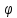
А

о 1 х

Если на ряду с поляр. координатами т. М(ρ,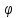) рассмотреть ее прямоуг. М(х,у) так называемых совмещенных полярный О ρ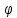и прямоуг. Оху систем координат, то прямоуг. координаты выраж. формулами:

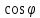х= ρ, у= ρ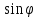

Полярный r ρ т. М(ρ,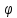) через декартовые координаты х и у находятся: ρ=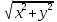

А полярный угол 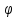из системы тригонометрических уравнений:

=

=

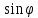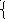
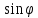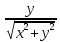
5. Прямоугольные декартовые координаты пространств.

Пям.дек.сист.коорд. в пространстве определяется заданием масштаба и 3-ех пересекающихся в одной точке взаимно перпендикулярных осей, занумерованных в определенном порядке. Точка пересечение осей – начало координат, сами оси – координатными осями, первая из них осью абсцисс, вторая – осью координат, третья – осью аппликат.

1. z

Оуz

Оxz

(2)

(3)

Оху

(1)–ось аппликат

(2)–ось ординат

(3)– ось абсцисс

Обозначим начало координат буквой О. Координатные оси будем соответственно обозначать через Ох,Оу и Оz. Координатные плоскости обозначим Оху, Oyz, Oxz, а прямоугольную декартовую сист. координат в пространстве – Оxyz.

6. Уравнение линии как геометрического места точек на плоскости. Общее уравнение прямой. Другие виды уравнения прямой на плоскости (уравнение прямой с угловым коэффициентом; уравнение прямой с данным угловым коэффициентом и проходящей через данную точку; уравнение прямой, проходящей через две данные точки; уравнение прямой в «отрезках»).

Уравнение линии как геометрического места точек на плоскости. Уравнение линии на плоскости относительно системы координат называется такое уравнение с 2умя переменными, которое удовлетворяет координатам любой точки на этой линии и не удовлетворяет координатам ни одной точки, не лежащей на данной линии.

Уравнение линии в декартовой координате имеет вид :

F (x, y) =0, где F (x, y) – функция переменных x, y

Уравнение линии в полярной координате имеет вид:

Ф (p, ϕ) =0, где Ф (p, ϕ) – функция переменных p, ϕ, при p ≥ 0 -β <ϕ ≤ π

При составлении уравнения линии целесообразно придерживаться следующей схемой:

• в выбранной системе координат взять точку М, считать что она принадлежит рассмотренной линии ( эту точку называют текущей, а ее координаты текущими).

• составить соотношение между текущими координатами на основе свойств определяющих рассматриваемую линию.

Общее уравнение прямой. Если на плоскости введена прямоугольная декартова система координат, то

Ax + By + C=0 (1), в котором пара А и В одновременно не равны 0

А²+ В² ≠ 0 (2)

Верно и обратное утверждение: в прямоугольной декартовой системе ОХУ всякая прямая может быть представлена линейным уравнением вида.

Уравнение (1) – общее уравнение прямой.

Частные виды прямой:

• если С=0, то Ах + Ву = 0 (проходит через начало координат)

• если А=0, то Ву + С = 0 (параллельно оси Ох)

• если В=0, то Ах + С = 0 (параллельно оси Оу)

• если А=С=0, то у=0 (совпадает с осью Ох)

• если В=С=0, то х=0 (совпадает с осью Оу)

Другие виды уравнения прямой на плоскости.

у АПрямая проходящая через точку А (а, 0) оси Ох и ǁ оси Оу.

Направление любой прямой непараллельно оси Оу характеризует ее угловой

а коэффициент k, который равен tg угла наклона α этой прямой к положению оси Ох,

Рис. 1 т.е. k = tg*α; где 0 ≤ α < π

Прямая Ох угловой коэффициент не имеет.

Уравнение прямой имеет угловой коэффициент k и пересекает ось ординат в точке

y В (0, b) и пересекает ось Оу в В (b, b)

bBy = kx + b и называется уравнением прямой с угловым коэффициентом.

Рис. 2

Уравнение прямой имеет угловой коэффициент k и проходит через точку М₀ (х₀; у₀) имеет вид у - у₀ = k (х – х₀)

Уравнение прямой, проходящая через две точки М₁ (х₁; у₁) и М₂ (х₂; у₂) с разными абсциссами х₁≠х₂ и разными ординатами у₁≠у₂: у – у₁ \ у₂ – у₁ = х – х₁ \ х₂ – х₁

У Пусть прямая пересекает ось Ох в точке А(а; 0) и ось Оу в точке В (0;в), причем

В в а≠0 и в≠0, т.е. прямая не параллельна координатным осям и не проходит через

А х начало координат, тогда уравнение:

х\а + у\в = 1 – уравнение прямой в «отрезках».