
shpory_po_matem1
.docx2.Понятие функции. График функции. Пусть Х и У-два произв. множества действ.чисел,если каждому элементу х из множ.Х по некорот. правилу f поставлен в соотв. вполне опред.эл-т у из множ.У ,то –задана функция f и исп.след.обозн. y=f(x). переменная х наз. независимой переменной или аргументом ф-ции, переменная у-зависимая переменная или ф-ция. Ф-ция,все значения кот. равны м\у собой наз.посмтоянной и обозн.С. Ф-ция f,определенная на множ.Х наз.ограниченной, если сущ.М>0,такое что все х из множ.Х: |f(x)|<=M. Ф.f(x)наз. возрастающей(убыв.)на множ.Х,если для люб.знач.х1 и х2 ,таких ,что х2>х1,из этого множ.выполн.нер-во: f(x2)>f(x1) (f(x2)<f(x1)).Если для люб. х2>х1 выполн. f(x2)>=f(x1)( f(x2)<=f(x1)),то ф. наз.неубыв.(невозр.). Данные ф-ции наз.монотонные. Графиком ф-ции наз. множ.всех точен плоскости с корд. (х, f(x)),т.е. корд. х и у связаны соотнош. y=f(x).
3.Предел
последовательности.Свойства сходящихся
последовательностей.Число
а наз. пределом последовательности,если
для любого Е>0 сущ.
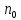 из n
€ N,такое
что для люб n>
из n
€ N,такое
что для люб n> выполн. неравенство
выполн. неравенство
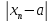 <
Е и обозн. а=
<
Е и обозн. а=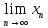 .Геометрически
это обозн.,что в любой Е окресности
точки а находятся все члены
послеловательности начиная с некоторого
номера n.Свойства
сходящихся последовательностей:1)Для
того,чтобы число а было пределом
последовательности
.Геометрически
это обозн.,что в любой Е окресности
точки а находятся все члены
послеловательности начиная с некоторого
номера n.Свойства
сходящихся последовательностей:1)Для
того,чтобы число а было пределом
последовательности
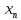 необходимо и достаточно,чтобы
необходимо и достаточно,чтобы
 имело
вид
имело
вид
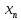 =а+
=а+ 2)Сводящ.
послед. имеет только 1 предел3)Сводящ.
послед. ограничена4)Пусть
2)Сводящ.
послед. имеет только 1 предел3)Сводящ.
послед. ограничена4)Пусть
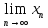 =a
и
=a
и
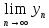 =b,
тогда
=b,
тогда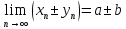
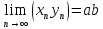
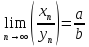 (b
(b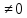 )
)
4.
Предел функции в точке. Односторонние
пределы.Число
В наз. пределом функции f
в точке х=а(или при х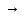 а),
если для любой последовательности {
а),
если для любой последовательности {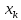 }, сходящейся к а, соответствующая
последовательность значений функции
{ f(
}, сходящейся к а, соответствующая
последовательность значений функции
{ f(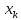 }
сходится к b.Для
обозначения функции f
в точке х=а используется запись
}
сходится к b.Для
обозначения функции f
в точке х=а используется запись
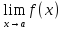 =b
– определение предела функции по
Гейне.Односторонние
пределыЧисло
b
наз. правым пределом в точке х=а, если
для любой сходящейся к а последовательности
{
=b
– определение предела функции по
Гейне.Односторонние
пределыЧисло
b
наз. правым пределом в точке х=а, если
для любой сходящейся к а последовательности
{
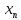 },
члены кот. больше или равны а,
соответствующая последовательность
{ f(
},
члены кот. больше или равны а,
соответствующая последовательность
{ f( }
сходится к b,
обозначается:
}
сходится к b,
обозначается:
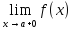 =b
Правый и левый предел функции в точке
наз. односторонними. В случае, когда
а=0, исп. Обозначение:
=b
Правый и левый предел функции в точке
наз. односторонними. В случае, когда
а=0, исп. Обозначение: ,
,
 .
Очевидно,
если сущ-ет
.
Очевидно,
если сущ-ет
 =b,
то сущ-ет и оба односторонних предела,
причём b
совпадает с ними.Справедливо и обратное
утверждение: если сущ-ют оба односторонних
f(a-0),
f(a+0)
и они равны, то сущ-ет предел
=b,
то сущ-ет и оба односторонних предела,
причём b
совпадает с ними.Справедливо и обратное
утверждение: если сущ-ют оба односторонних
f(a-0),
f(a+0)
и они равны, то сущ-ет предел
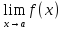 =b
и при этом b=
f(a-0)=
f(a+0)
. Если же односторонние пределы не
равны, т.е. f(a-0)
=b
и при этом b=
f(a-0)=
f(a+0)
. Если же односторонние пределы не
равны, т.е. f(a-0)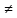 f(a+0),
то и предел
f(a+0),
то и предел
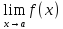 не сущ-ет.
не сущ-ет.
5.предел функции при x->∞. Свойства предела функции. Правило Лопиталя.
Число
b
наз.пределом f(x)
при x-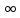 если для любой бесконеч.большой
последоват.Хn соответствующ . последовател.
знач.ф-ции f{(хn)} сходятся к b и
обознач.limf(х)=b.
если для любой бесконеч.большой
последоват.Хn соответствующ . последовател.
знач.ф-ции f{(хn)} сходятся к b и
обознач.limf(х)=b.
Ф-ция наз.бесконеч.малой при х-а асли предел limf(х)=0.
Ф-ция
наз.бесконеч.
большой при
х-а,если limf(х)=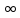 .
.
Св-ва:1)Предел
(сум./раз.)= (сумб/раз) пределаlim(f(х)+-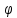 (х)=
limf(х)+-lim
(х)=
limf(х)+-lim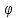 (х).След-е1
Ф-ция
может иметь только 1 предел в т.х=а.2)предел
произвед.2-х ф-ций=произвед.их пределов
lim(f(х)*
(х).След-е1
Ф-ция
может иметь только 1 предел в т.х=а.2)предел
произвед.2-х ф-ций=произвед.их пределов
lim(f(х)*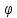 (х))=lim
(х))=lim
f(х)*lim (х).След-е2
а)постоян . множитель можно вынасить
за знак предела.б)предел степени с
натурал.показателем=той же степени
предела.3)предел
дроби=пределу чеслителя деленному на
предел знаменат.,если предел знамен.не
равен 0. limf(х)/
(х).След-е2
а)постоян . множитель можно вынасить
за знак предела.б)предел степени с
натурал.показателем=той же степени
предела.3)предел
дроби=пределу чеслителя деленному на
предел знаменат.,если предел знамен.не
равен 0. limf(х)/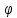 (х)=
(х)= f(х)/lim
f(х)/lim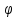 (х).
(х).
Прав.Лопиталя-м-д
нахождения пределов ф-ий, раскрывающий
неопределённости вида0/0 и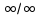 . Обосновывающая м-д теорема утверждает,
что при некоторых усл. предел отношения
ф-ий =пределу отношения их производных.
. Обосновывающая м-д теорема утверждает,
что при некоторых усл. предел отношения
ф-ий =пределу отношения их производных.
6.
Непрерывность функции.
Пусть функция f(x)
определена в некоторой окрестности
точки x=a.
Функция f(x) назыв непрерывной в точке
а, если
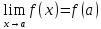 (1).
Равенство (1) означает выполнение трёх
условий: 1. Функция f(x) определена в точке
х=а и в некоторой её окрестности; 2.
Функция f(x) имеет предел при х→а; 3.
Предел функции f(x) в точке а равен
значению функции в этой точке. Т.к.
(1).
Равенство (1) означает выполнение трёх
условий: 1. Функция f(x) определена в точке
х=а и в некоторой её окрестности; 2.
Функция f(x) имеет предел при х→а; 3.
Предел функции f(x) в точке а равен
значению функции в этой точке. Т.к.
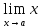 =а,
то равенство (1) можно записать в виде
=а,
то равенство (1) можно записать в виде
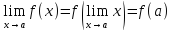 .
Это означает, что при нахождении предела
непрерывной функции f(x) можно перейти
к пределу под знаком функции, т.е. в
функцию f(x) вместо аргумента х можно
подставить его предельное значение.
Для того, чтобы функция f(x) была непрерывной
в точке а, необходимо и достаточно чтобы
она была непрерывной в этой точке слева
и справа. Приведём ещё одно определение
функции, непрерывной в точке а. Равенство
(1) равносильно:
.
Это означает, что при нахождении предела
непрерывной функции f(x) можно перейти
к пределу под знаком функции, т.е. в
функцию f(x) вместо аргумента х можно
подставить его предельное значение.
Для того, чтобы функция f(x) была непрерывной
в точке а, необходимо и достаточно чтобы
она была непрерывной в этой точке слева
и справа. Приведём ещё одно определение
функции, непрерывной в точке а. Равенство
(1) равносильно:
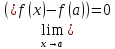 .
если учесть , что соотношения х→а и
(х-а)→0 также равносильны, то получим,
что условие непрерывности функции f(x)
в точке а записывается в виде
.
если учесть , что соотношения х→а и
(х-а)→0 также равносильны, то получим,
что условие непрерывности функции f(x)
в точке а записывается в виде
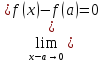 (2)
.
опр. Прирощением независимой переменной
х в точке а можно записать:
(2)
.
опр. Прирощением независимой переменной
х в точке а можно записать:
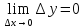 (3).
Тогда новое определение непрерывности
функции: функция f(x) назыв непрерывной
в точке а, если её приращение в этой
точке есть бесконечно малая функция.Опр.
Функция f(x) назыв непрерывной на интервале
(а;в), если она непрерывна в каждой точке
х
(3).
Тогда новое определение непрерывности
функции: функция f(x) назыв непрерывной
в точке а, если её приращение в этой
точке есть бесконечно малая функция.Опр.
Функция f(x) назыв непрерывной на интервале
(а;в), если она непрерывна в каждой точке
х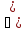 а;в).
Если же, кроме того, функция f(x) непрерывна
в точке а слева, а в точке в – справа,
то функция f(x) назыв непрерывной на
отрезке [a;в].
Опр. Функция f(x) назыв кусочно-непрерывной
на отрезке [a;в], если она непрерывна во
всех внутренних точках [a;в], за исключением
конечного числа точек, в которых она
имеет разрывы первого рода, а в точках
а и в имеет соответствующие односторонние
пределы.
а;в).
Если же, кроме того, функция f(x) непрерывна
в точке а слева, а в точке в – справа,
то функция f(x) назыв непрерывной на
отрезке [a;в].
Опр. Функция f(x) назыв кусочно-непрерывной
на отрезке [a;в], если она непрерывна во
всех внутренних точках [a;в], за исключением
конечного числа точек, в которых она
имеет разрывы первого рода, а в точках
а и в имеет соответствующие односторонние
пределы.
8.Понятие
производной функции. Геометрический
смысл производной.
Производная функция y=f(x)
в точке x=a
- предел отношения приращения функции
в точке x=a
к приращению аргумента если ∆x→0.обозначают
f'(a),
y'(a).
Согласно определению f'(a)=
LimΔx→0f((a+Δx)-f(a))/Δx
(1) Операция нахождения производной –
дифференцирование. Теорема:
если функция y=f(x)
в точке x
имеет производную, то она непрерывна
в этой точке.Геометрический
смысл: пусть
y=f(x)
определена на интервале (a;b)
и пусть кривая AB-график
этой функции. Пусть точка М
(x0;f(x0))-произвольная
точка графика. Придадим аргументу x0
приращение ∆x.
Соответствующую точку на графике
обозначим через Р(x0+∆x
;f(x0+∆x)).
Через точки М и Р построим секущую.найдём
угловой коэффициент секущей. Понятно,
что k=tg![]() NMP=∆f/∆x.
если точку Р устремить по кривой к точке
М то положение секущей МР будет
изменяться. Если ∆x→0
и существует предельное положение
секущей, то полученная прямая наз.
касательной
к графику функции y=f(x)
в точке x0.
Понятно, что условием существования
предельного положения секущей является
существование предела kкас=
LimΔx→0∆f/∆x=
LimΔx→0k∆x=
f'(x0)
график функции имеет касательную в
точке x0
тогда и
только тогда, когда функция дифференцируема
в этой точке и f'(x0)-угловой
коэффициент касательной.
Тогда уравнение касательной в точке
М0(x0;y0)
– y-y0=
f'(x0)(x-x0)
(2) прямая проходящая через точку (x0;y0)
и перпендикулярная касательной –
нормаль к
графику функции,
и учитывая условия перпендикулярности
двух прямых и формулу(2) имеет вид:
y-y0=(-1/
f'(x0))*
(x-x0)
если f'(x0)=0,
то уравнение нормали: x=x0
NMP=∆f/∆x.
если точку Р устремить по кривой к точке
М то положение секущей МР будет
изменяться. Если ∆x→0
и существует предельное положение
секущей, то полученная прямая наз.
касательной
к графику функции y=f(x)
в точке x0.
Понятно, что условием существования
предельного положения секущей является
существование предела kкас=
LimΔx→0∆f/∆x=
LimΔx→0k∆x=
f'(x0)
график функции имеет касательную в
точке x0
тогда и
только тогда, когда функция дифференцируема
в этой точке и f'(x0)-угловой
коэффициент касательной.
Тогда уравнение касательной в точке
М0(x0;y0)
– y-y0=
f'(x0)(x-x0)
(2) прямая проходящая через точку (x0;y0)
и перпендикулярная касательной –
нормаль к
графику функции,
и учитывая условия перпендикулярности
двух прямых и формулу(2) имеет вид:
y-y0=(-1/
f'(x0))*
(x-x0)
если f'(x0)=0,
то уравнение нормали: x=x0
9. Физический смысл производной. Правило дифференцирования.Пусть некоторая материальная точка m движется прямолинейно и и задан з-н его движ. s=s(t) т.е известен путь которая прошла точка m от некоторой начальной точки отсчёта в момент вр.(t). Тогда в момент вр.(to)точка пройдёт расстояние s(to),а в момент вр. to+^t- расстояние s((to)+(^t)) за промежуток вр. ^t точка пройдёт расстояние ^s=s(to+^t)-s(to). Отношение ^s/^t можно рассм.как среднюю скорость движ. на промежутке вр.to;(to+^t). И чем меньше промежуток вр. ^t,тем точнее соотв. средняя скорость будет х-ть движ. точки в момент вр. to. Поэтому предел средней скорости движ. при ^t=0 наз. скоростью движ. точки m в момент вр.(to). И обознач. v(to) : V(to)=lim s(to+^t)-s(t0)/^t=s’(to) Таким образом, скорость движ. в момент вр.to есть производная пути по вр.Правило дифференцированияЕсли функция u=u(x) и v=v(x) имеет производные в точке x,то сумма, разность, произведение и частное этих функции также имеет произв. В данной точке. (u+-v)’=u’+-v’;(uv’)=u’v+v’u;(u/v)’=u’v-v’u/v2Утверждение. Если ф-ция y=f(x) строго монотонна и непрерывна в некоторой окрестности точки xo, имеем производную в точке xo и f’(xo)не равно нулю, то обратная ф-ция x=f-1(y) имеет в соотв.точке yo, yo=f(xo),причём (f-1)(yo)=1/f’(xo)Утверждение. Если ф-ция u=m(x) имеет в точке xo произвольную, а ф-ция y=f(u) имеет соотв.точки (uo=m(xo)),производную f’(uo),то сложная ф-ция y=f(m(x)) имеет произв.в точке xo и справедлива формула:y’(xo)=f’(uo)m’(xo) (где m- фи)
10.Производная
сложной функции.Логарифмическая
производная.Таблица производных.Если
функция u=Ф(x)
имеет в т.X
0
производную y=f(u),
а функция имеет в соотв. Точке u
0
=Ф(X
0)производную
f’(ф0),
то сложная функция y=f(Ф(x))
имеет производную в точке X
0
и справедлива формула: y’(X
0)=f’(u
0 )*ф’(X
0)
Логарифмическая производная:Пусть
f(x)>0
, тогда рассмотрим функцию y=
ln(f(x))
. диф-ем эту функцию, как сложную где y=
lnu,
u=f(x)
получим (ln(f(x)))’=(lnu)’*f’(x)*f’(x)/f(x)Производная
от лог некоторой функции наз лог
производной этой ф-ции,
а послед применение операции
логарифмирования , а затем диф-ния наз
лог
диференциаломТабл:
1)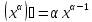 ;
2)
;
2)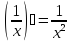 ; 3) (
; 3) ( =
=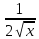 ;
4)
;
4)
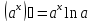 ;
5)
;
5)
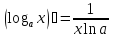 ; 6)
; 6)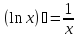 ;
7)
;
7)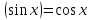 ;8)
(
;8)
(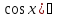 =
-
=
-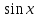 ;
9)(tgx
;
9)(tgx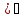 =
=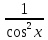 ;10)(ctgx
;10)(ctgx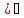 =
=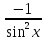 ;
11)(arcsinx
;
11)(arcsinx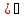 =
=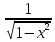 ;
12)(arccosx
;
12)(arccosx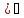 =
-
=
-
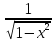 .
.
11.Понятие
диф-ти функции в точке. Диф. функция.
Таблица диф-лов.Функция
у=f(х)
наз. Дифференцируемой в точке х, если
ее произведение
 у
в этой точке можно представить в
виде:
у
в этой точке можно представить в
виде: у=А
у=А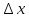 +
+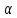 (
( )
) (1) ,где А-некоторое число,
(1) ,где А-некоторое число,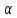 (
(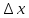 )-бесконечно
малая функция при х
)-бесконечно
малая функция при х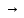 0.
Теорема:для того чтобы функция у=f(х)
была дифференцируемой в точке х,необходимо
и достаточно чтобы она имела в этой
точке производную f
0.
Теорема:для того чтобы функция у=f(х)
была дифференцируемой в точке х,необходимо
и достаточно чтобы она имела в этой
точке производную f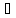 (х).Пусть
функция у=f(х)
дифференцируема в точке х.Тогда
прирощение функции может быть записано
по формуле (1),где
(х).Пусть
функция у=f(х)
дифференцируема в точке х.Тогда
прирощение функции может быть записано
по формуле (1),где
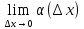 =0.Тогда
=0.Тогда
 (
(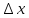 )
)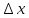 -бесконечно малая функцияболее ысокого
порядкапо сравнению с А*
-бесконечно малая функцияболее ысокого
порядкапо сравнению с А* .Тогда
.Тогда
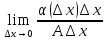 =
=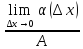 =0.
Поэтому правое слагаемое в формуле (1)
явл.главной частью прирощения
=0.
Поэтому правое слагаемое в формуле (1)
явл.главной частью прирощения
 у
при чем она линейная относительно
у
при чем она линейная относительно
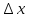 ,наз
дифференциалом функции у=f(х)
в точке х.Для обозначения используют
обозначение dy=A
,наз
дифференциалом функции у=f(х)
в точке х.Для обозначения используют
обозначение dy=A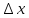 ,и т.к. А=
f
,и т.к. А=
f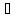 (х),то
dy=
А
(х),то
dy=
А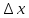 =
f
=
f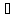 (х)dx
(2).Таблица
дифференциалов:Согласно формуле(2)
можно из табл. Производных получить
аналогичную табл. дифференциалов.Так
из формулы (uv
(х)dx
(2).Таблица
дифференциалов:Согласно формуле(2)
можно из табл. Производных получить
аналогичную табл. дифференциалов.Так
из формулы (uv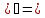 u
u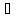 v+uv
v+uv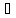 умножив обе части на dx
получим: (uv
умножив обе части на dx
получим: (uv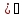 dx=u᾽dx*v+u*v
dx=u᾽dx*v+u*v dx.
Табл: 1)
dx.
Табл: 1)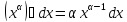 ; 2)
; 2)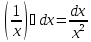 ; 3) (
; 3) (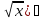 dx=
dx=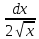 ;
4)
;
4)
 ;
5)
;
5)
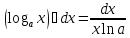 ; 6)
; 6)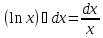 ;
7)
;
7)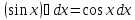 ;8)
(
;8)
(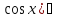 dx=
-
dx=
- ;
9)(tgx
;
9)(tgx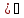 dx=
dx=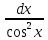 ;10)(ctgx
;10)(ctgx dx=
dx=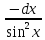 ;
11)(arcsinx
;
11)(arcsinx dx=
dx=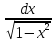 ;
12)(arccosx
;
12)(arccosx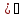 dx=
-
dx=
-
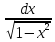 .
.
12.Геометрический
и механический смысл дифференциала.Инвариантность
формы диф-лаю табл диф-лов.Геометрический
смысл дифференциала функции Выясним
геометрический смысл дифференциала.
Для этого проведём к графику функции
у = f (х) в точке М (х; у) касательную МТ и
рассмотрим ординату этой касательной
для точки х + Δх (рис. 2). На рисунке
 АМ
АМ = Δх,
= Δх,
 АМ1
АМ1 = Δу. Из прямоугольного треугольника
МАВ имеем: tg
α =AB/Δx,
т.е.
= Δу. Из прямоугольного треугольника
МАВ имеем: tg
α =AB/Δx,
т.е.
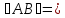 tg α ⋅Δх.Но,
согласно геометрическому смыслу
производной, tg
α
= f
′
(х). Поэтому АВ = f
′
(х)⋅Δх.
Сравнивая
полученный результат с формулой получаем
dy
= АВ, т.е. дифференциал функции у = f
(х) в точке х равен приращению ординаты
касательной к графику функции в этой
точке, когда х получит приращение Δх.
tg α ⋅Δх.Но,
согласно геометрическому смыслу
производной, tg
α
= f
′
(х). Поэтому АВ = f
′
(х)⋅Δх.
Сравнивая
полученный результат с формулой получаем
dy
= АВ, т.е. дифференциал функции у = f
(х) в точке х равен приращению ординаты
касательной к графику функции в этой
точке, когда х получит приращение Δх.

Табл:
1)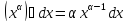 ; 2)
; 2) ; 3) (
; 3) (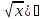 dx=
dx=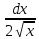 ;
4)
;
4)
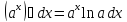 ;
5)
;
5)
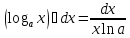 ; 6)
; 6)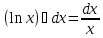 ;
7)
;
7) ;8)
(
;8)
(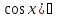 dx=
-
dx=
-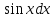 ;
9)(tgx
;
9)(tgx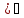 dx=
dx=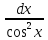 ;10)(ctgx
;10)(ctgx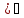 dx=
dx=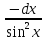 ;
11)(arcsinx
;
11)(arcsinx dx=
dx=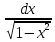 ;
12)(arccosx
;
12)(arccosx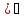 dx=
-
dx=
-
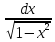 .
.
14. Исследование функции с помощью производной. 1Найти область определения функции, точки разрыва функции и интервалы непрерывности 2Найти (если это возможно) точки пересечения графика с осями оординат. 3Найти интервалы знакопостоянства функции (промежутки, на которых f (x) > 0 или f (x) < 0). 4Решить вопрос о чётности, нечётности, симметрии, периодичности функции. 5Если есть точки разрыва 2-го рода, найти вертикальные асимптоты. 6Найти, если они есть, наклонные и горизонтальные асимптоты. 7С помощью 1-ой производной найти точки экстремума и области возрастания и убывания 8данной функции. Найти экстремальные значения функции. 9С помощью 2-ой производной найти точки перегиба, области выпуклости и вогнутости. 10Построить график.
15.Понятие
первообразной функции.
Основной операцией дифференциального
исчисления явл. отыскание первообразной
заданной функции. Восстановление
функции по известной производной этой
функции есть одна из задач интегрального
исчисления. Функция F(x)
наз. первообразной для функции f(x)
на некотором промежутке Х, если для
любого х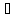 Х
выполняется F,(x)=f(x)
. Утверждение : Если F1(x)и
F2(x)
– 2 первообразные для функции f(x)на
промежутке Х , то они отличаются лишь
на постоянную , т.е. F1(x)-F2(x)=C,
где С- некоторая постоянная. Другими
словами, если F(x)есть
первообразная для функции f(x),то
множество функций F(x)+С
включает все первообразные для данной
функции f(x).Замечание
: Ранее было показано, что не все функции,
заданные на каком-либо интервале
Х=(а;в) имеют первообразную . Аналогично,
не всякая функция имеет первообразную.
Х
выполняется F,(x)=f(x)
. Утверждение : Если F1(x)и
F2(x)
– 2 первообразные для функции f(x)на
промежутке Х , то они отличаются лишь
на постоянную , т.е. F1(x)-F2(x)=C,
где С- некоторая постоянная. Другими
словами, если F(x)есть
первообразная для функции f(x),то
множество функций F(x)+С
включает все первообразные для данной
функции f(x).Замечание
: Ранее было показано, что не все функции,
заданные на каком-либо интервале
Х=(а;в) имеют первообразную . Аналогично,
не всякая функция имеет первообразную.
16.
Неопределенный интеграл. Множество
всех первообразных функций f(x)
называется неопределенным интегралом
функции f(x)
и обозначается
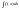 .
Функция f(x)
называется подынтегральной функцией,
f(x)dx
– подынтегральное выражение, переменная
х – переменная интегрирования. Итак,
если F(х)
– первообразная функции f(х)
на промежутке X,
то интеграл
.
Функция f(x)
называется подынтегральной функцией,
f(x)dx
– подынтегральное выражение, переменная
х – переменная интегрирования. Итак,
если F(х)
– первообразная функции f(х)
на промежутке X,
то интеграл
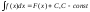 .Подчеркнем,
что символ
.Подчеркнем,
что символ
 обозначает совокупность всех первообразных
для функции f(x).
Отыскание неопределенного интеграла
по известной подынтегральной функции
называется интегрированием этой
функции. Свойства неопределенного
интеграла: Если функция f
дифференцируема на некотором промежутке,
то на нем выполняется:
обозначает совокупность всех первообразных
для функции f(x).
Отыскание неопределенного интеграла
по известной подынтегральной функции
называется интегрированием этой
функции. Свойства неопределенного
интеграла: Если функция f
дифференцируема на некотором промежутке,
то на нем выполняется:
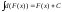 или
или
 ;
;
Пусть
функция f(x)
имеет первообразную на некотором
промежутке I,
тогда для всех х из промежутка I
выполняется равенство:
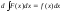 ;
;
Если
ф-ция f
имеет первообразную на промежутке I
и k
– число, но ф-ция
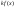 также имеет на промежутке I
первообразную, причем при
также имеет на промежутке I
первообразную, причем при
 справедливо равенство:
справедливо равенство:
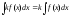 ;
;
Неопределенный
интеграл от суммы двух ф-ций равен сумме
интегралов от этих ф-ций:
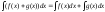 .
.
17.Таблица интегралов.Основные методы интег-ния:замена переменной, интег-ние по частям.
Метод замены переменной:Под знаком интеграла может оказаться функция, для которой нет табличного интеграла и непосредств. интегриров. Невозможно. В таком случае используют другие приёмы в частности, метод замены переменной. Далее для удобства изложения запись Ф(х) =ф(t) будет опред. функцию Ф(ф(t)). Утверждение1:Пусть функция х=ф(t) определена и дифференцируема на промежутке T,а Х-множество её значений. Пусть функция у=f(x) определена на множества Х и имеет на этом промеж. первообразную тогда справедливо формула: ∫f(x)dx x=ф(t)=∫f(ф(t))ф’(t)dt, которая наз.формулой замены переменной в неопределённом интеграле.Интегрир. по частямУтверждение2:Пусть функции u=u(x) и v=v(x), дифферен. на промежутке Х и пусть существ.∫v(x)u’(x)dx. Тогда существ. ∫v’(x)u(x)dx И справедливо формула 2: ∫u(x)v’(x)dx=u(x)*v(x)-∫v(x)u’(x)dx.Таблица интегралов: Таблица:1)∫хαdx=xα+1/α+1+C;2)∫dx/x=ln|x|+c;3)∫axdx=ax/lna+c;4)∫exdx=ex+c;5)∫sinxdx=-cosx+c; 6)∫cosxdx=sinx+c;7)∫dx/cos2x=tgx+c;8)∫dx/sin2x=-ctgx+c;9) ∫tgxdx=-ln|cosx|+c; 10) ∫ctgxdx=ln|sinx|+c;11) ∫dx/a2+x2=1/a*arctgx/a+c;12) ∫dx/x2-a2=1/2a*ln|x-a/x+a|+c; 13) ∫dx/√a2-x2=arcsinx/a+c;14)∫dx/√x2±a2=ln|x+√x2±a2|+c
18.
Таблица интегралов.
Интег-ние рац-ных и иррац-ных
функций.Интегрирование
рац ф-ций.
Определение: Элементарными называются
дроби следующих четырех типов: I.
1/ax+bII.
1/
(ax +b)m
III. Mx+N/(ax2+bx+c) IV. Mx+N/(ax2+bx+c)
n
m, n –
натуральные числа (m ≥ 2, n ≥ 2) и b2 – 4ac
<0.Первые два типа интегралов от
элементарных дробей довольно просто
приводятся к табличным подстановкой
t = ax + b. 1) .
.
2)
Интегрирование рациональных дробей : Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби. Теорема: Если R(x)=Q(x)/P(x) = - правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)α…(x - b)β(x2 + px + q)λ…(x2 + rx + s)μ), то эта дробь может быть разложена на элементарные по следующей схеме: где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины. При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х. Применение этого метода рассмотрим на конкретном примере. Таблица:1)∫хαdx=xα+1/α+1+C;2)∫dx/x=ln|x|+c;3)∫axdx=ax/lna+c;4)∫exdx=ex+c;5)∫sinxdx=-cosx+c; 6)∫cosxdx=sinx+c;7)∫dx/cos2x=tgx+c;8)∫dx/sin2x=-ctgx+c;9) ∫tgxdx=-ln|cosx|+c; 10) ∫ctgxdx=ln|sinx|+c;11) ∫dx/a2+x2=1/a*arctgx/a+c;12) ∫dx/x2-a2=1/2a*ln|x-a/x+a|+c; 13) ∫dx/√a2-x2=arcsinx/a+c;14)∫dx/√x2±a2=ln|x+√x2±a2|+c
19.Интегралы с квадратичной иррациональностью. Интег-ние тригоном. функции диф-ного бинома.
1)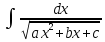 ,где
а≠0.Путём
дополнения квадратного трёхчлена
,где
а≠0.Путём
дополнения квадратного трёхчлена
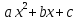 до полного квадрата,приводится в
зависимости от знака aк
одному из табличных интегралов.
до полного квадрата,приводится в
зависимости от знака aк
одному из табличных интегралов.
2)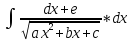 ,где
ad≠0.
Можно привести к интегралу (9):
,где
ad≠0.
Можно привести к интегралу (9):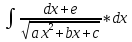 =
=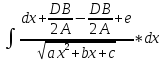 =
=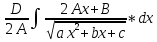 +
+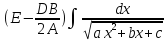 =
=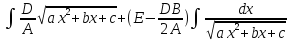
3)Вычислим
интеграл: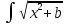 *dx,b>0,
*dx,b>0,
 *dx,a≠0
(10)
*dx,a≠0
(10)
 *dx=
*dx=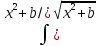 =
=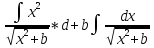 (11).
Выч. Интеграл
(11).
Выч. Интеграл
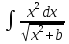 по частям. Пологая u=x,
du=
по частям. Пологая u=x,
du= ,
тогда du=dx,
v=
,
тогда du=dx,
v=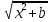 ,
тогда получим
,
тогда получим
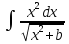 =x
=x *dx.
Подставляя в последнее выражение в
ф-лу (11) 2
*dx.
Подставляя в последнее выражение в
ф-лу (11) 2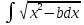 =x
=x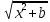 +b
+b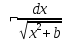 ,
,
Интег-ние
тригоном. функции диф-ного бинома.1)Интегралы
от квадратов и других чётных степеней
синуса и косинуса находят,применяя
следующие ф-лы понижения степени: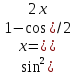 ;
;
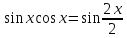 2)Интегралы
от кубов и других нечётных степеней
синуса и косинуса находят,отделяя от
нечётной степени один множитель и
пологая кофункцию равной новой переменной
u.Интеграл
2)Интегралы
от кубов и других нечётных степеней
синуса и косинуса находят,отделяя от
нечётной степени один множитель и
пологая кофункцию равной новой переменной
u.Интеграл
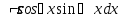 находятся по правилу 1), если d
и c
оба чётные и по правилу 2), если d
и c
нечётно.
находятся по правилу 1), если d
и c
оба чётные и по правилу 2), если d
и c
нечётно.
20.Определение
определённого интеграла. Основные
свойства определённого интеграла.Предел
от суммы
![]() при
при
![]() , если он существует и конечен, называется
определенным интегралом от функции
f(x)
в пределах от a
до b
и обозначается:
, если он существует и конечен, называется
определенным интегралом от функции
f(x)
в пределах от a
до b
и обозначается:![]() Если
существует определенный интеграл от
функции f(x)
, то в этом случае функция называется
интегрируемой на отрезке [a,b]
.Определенный интеграл от непрерывной
функции равен разности значений
первообразной функции при верхнем и
нижнем пределах.
Если
существует определенный интеграл от
функции f(x)
, то в этом случае функция называется
интегрируемой на отрезке [a,b]
.Определенный интеграл от непрерывной
функции равен разности значений
первообразной функции при верхнем и
нижнем пределах.![]()
Свойства:
![]()
![]()
![]()
