
Будылин А.М. Вариационное исчисление. 2001., 50 стр
.pdf
Вариационное исчисление
А.М.Будылин
budylin@mph.phys.spbu.ru
21 мая 2001 г.
Постановка некоторых . . .
Введение в вариационный метод
Уравнение Эйлера–Лагранжа Приложения Обобщения
Задачи на условный экстремум Первое необходимое условие . . .
Семейства экстремалей Динамика частиц Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 1 из 197
Назад
Полный экран
Закрыть
Выход

Часть I
Необходимые условия экстремума
Постановка некоторых вариационных задач
Отыскание геодезических
На плоскости
На произвольной поверхности
Задача о брахистохроне
Задача о наименьшей поверхности
Катеноид
Проблема Плато
Простейшая вариационная задача
Простейшая изопериметрическая задача
Задача навигации
Введение в вариационный метод
Происхождение названия «вариационное исчисление»
Современная терминология
Основная лемма
Основной вариант
Обобщение по гладкости
Постановка некоторых . . .
Введение в вариационный метод Уравнение Эйлера–Лагранжа
Приложения
Обобщения
Задачи на условный экстремум Первое необходимое условие . . .
Семейства экстремалей
Динамика частиц
Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 2 из 197
Назад
Полный экран
Закрыть
Выход

Обобщение на кратные интеграла
Лемма Дюбуа–Реймона
Уравнение Эйлера–Лагранжа
Постановка вопроса
Вариация интегрального функционала
Экскурс в дифференциальное исчисление
Дифференцирование интеграла по параметру
Цепное правило
Уравнение Эйлера–Лагранжа
Вывод уравнения
Замечания
Анализ уравнения Эйлера–Лагранжа
Fне зависит от y
Fне зависит от x
Случай полной производной F = dxd G(x, y)
Приложения
Геодезические
Уравнение Эйлера
Частный случай, первый вариант
Частный случай, второй вариант
Геодезические на сфере
Постановка некоторых . . .
Введение в вариационный метод
Уравнение Эйлера–Лагранжа
Приложения
Обобщения Задачи на условный экстремум
Первое необходимое условие . . .
Семейства экстремалей
Динамика частиц Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 3 из 197
Назад
Полный экран
Закрыть
Выход

Геодезические на поверхности вращения
Брахистохрона
Минимальная поверхность вращения
Катеноид
Огибающая
Геометрическая оптика
Обобщения
Случай нескольких искомых функций
Параметрическое представление
Случай производных высших порядков
Свободные концы
Естественные условия
Задача о навигации
Условие трансверсальности
Случай кратных интегралов
Экстремали двойного интеграла
Экстремали тройного интеграла
Задачи на условный экстремум
Изопериметрическая задача
Простейшая изопериметрическая задача
Прямые обобщения
Постановка некоторых . . .
Введение в вариационный метод
Уравнение Эйлера–Лагранжа Приложения
Обобщения
Задачи на условный экстремум
Первое необходимое условие . . .
Семейства экстремалей
Динамика частиц Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 4 из 197
Назад
Полный экран
Закрыть
Выход

Задача Дидоны
Задача Лагранжа
Простейший случай
Отыскание геодезических
Общий случай
Часть II. Достаточные условия экстремума
Часть III. Приложения
Предметный указатель
Постановка некоторых . . .
Введение в вариационный метод
Уравнение Эйлера–Лагранжа Приложения Обобщения
Задачи на условный экстремум Первое необходимое условие . . .
Семейства экстремалей
Динамика частиц
Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 5 из 197
Назад
Полный экран
Закрыть
Выход

1.Постановка некоторых вариационных задач
Чтобы получить представление о вариационных задачах, рассмотрим некоторые из них.
1.1.Отыскание геодезических
1.1.1. На плоскости
Начнем с элементарного вопроса: что представляет собой плоская кривая наименьшей длины, соединяющая две фиксированные точки плоскости?
Для математической формулировки фиксируем две точки P1(x1, y1) и P2(x2, y2) на плоскости xy, считая x1 < x2, и рассмотрим гладкую кривую
y = y(x) , |
x [x1, x2] , |
|
(y2 |
= y(x2) , |
(1.1) |
y1 |
= y(x1) , |
|
соединяющей точки P1 и P2. Длина дуги кривой (1.1), как хорошо известно, равна
x2 |
|
|
|
|
I = Z |
|
|
|
|
|
1 + y02 |
dx . |
(1.2) |
|
x1 |
p |
|
||
Задача сводится к выбору функции y(x) так, чтобы интеграл (1.2) был наименьшим из возможных.
В постановке задачи мы наложили дополнительное ограничение (1.1), выражающееся в том, что y является однозначной функцией x. Это ограничение может быть
Постановка некоторых . . .
Введение в вариационный метод
Уравнение Эйлера–Лагранжа
Приложения
Обобщения
Задачи на условный экстремум
Первое необходимое условие . . .
Семейства экстремалей
Динамика частиц Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 6 из 197
Назад
Полный экран
Закрыть
Выход

снято переходом к параметрическому заданию кривой в форме
y = y(t) , |
t [t1, t2] , |
||
x = x(t) , |
|
||
(x2 |
= x(t2) , y2 |
(1.3) |
|
= y(t2) . |
|||
x1 |
= x(t1) , y1 |
= y(t1) , |
|
1.1.2.На произвольной поверхности
Менее тривиальный случай. Пусть фиксированы две точки некоторой (гладкой) поверхности, заданной, например, уравнением
g(x, y, z) = 0, . |
(1.4) |
Что представляет собой кривая наименьшей длины, лежащая на этой поверхности и соединяющая фиксированные точки? Именно такие кривые и называются геодезическими.
Для математической формулировки этой задачи будем считать, что поверх-
ность (1.4) может быть задана параметрически |
|
|
y = y(u, v) , |
(1.5) |
|
|
x = x(u, v) , |
|
z = z(u, v) .
Здесь u и v параметры, играющие роль координат на поверхности. Выразим квадрат дифференциала длины дуги в терминах дифференциалов u и v:
(ds)2 = (dx)2 + (dy)2 + (dz)2 , |
(1.6) |
Постановка некоторых . . .
Введение в вариационный метод
Уравнение Эйлера–Лагранжа
Приложения
Обобщения Задачи на условный экстремум
Первое необходимое условие . . .
Семейства экстремалей Динамика частиц Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 7 из 197
Назад
Полный экран
Закрыть
Выход

в терминах дифференциалов u и v: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
dx = |
|
∂x |
du + |
∂x |
dv , |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
(1.7) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
dy = ∂u du + |
∂v dv , |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
dz = |
|
∂z |
du + |
∂z |
dv , |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(ds)2 = P (u, v)(du)2 + 2Q(u, v)dudv + R(u, v)(dv)2 , |
(1.8) |
|||||||||||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∂x |
|
|
2 |
|
|
|
|
∂y |
|
2 |
|
|
|
|
|
∂z |
|
2 |
|
|
|
|||||||||
P = |
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
, |
|
|
|||||||||||
∂u |
|
|
∂u |
|
|
∂u |
|
|||||||||||||||||||||||||
|
∂x |
|
∂x |
∂y |
|
|
∂y |
|
|
∂z |
|
|
∂z |
(1.9) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Q = ∂u · ∂v + ∂u · ∂v + ∂u · ∂v , |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|
∂x |
|
|
2 |
|
|
|
|
∂y |
|
2 |
|
|
|
|
∂z |
2 |
|
|
|
|||||||||||
R = |
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
. |
|
|
||||||||||||||
∂v |
|
|
∂v |
|
|
∂v |
|
|
|
|||||||||||||||||||||||
Отметим. что если координаты (u,v) на поверхности ортогональны, то |
|
|||||||||||||||||||||||||||||||
Q = 0 |
|
|
|
(ортогональность) . |
(1.10) |
|||||||||||||||||||||||||||
Действительно, координатная сетка на поверхности задается кривыми u = Const и v = Const. Кривая u = u0 задается параметрически
x = x(u0, v) ,
y = y(u0, v) ,
z = z(u0, v) ,
Постановка некоторых . . .
Введение в вариационный метод
Уравнение Эйлера–Лагранжа
Приложения
Обобщения
Задачи на условный экстремум Первое необходимое условие . . .
Семейства экстремалей
Динамика частиц
Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 8 из 197
Назад
Полный экран
Закрыть
Выход

где роль параметра играет только переменная v. Вектор
t = |
|
∂x |
, |
∂y |
, |
∂z |
, |
t = t (v) , |
|
|
∂v |
||||||
→− |
∂v ∂v |
|
|
→− →− |
||||
направлен по касательной к этой кривой. Аналогично, касательным вектором к кри-
вой v = v0 с параметрическим заданием |
|
|
|
|||||||
|
|
|
y = y(u, v0) , |
|
||||||
|
|
|
|
x = x(u, v0) , |
|
|||||
|
|
|
z = z(u, v0) , |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
будет вектор |
|
|
|
|
|
|
|
|
|
|
s = |
∂x |
, |
∂y |
, |
∂z |
, |
|
s = s (u) . |
||
|
|
|
|
|||||||
→− |
∂u ∂u ∂u |
|
s |
→− →− |
||||||
|
|
|
|
|
|
|
|
|
→− |
|
В случае ортогональных координат векторы |
→− |
и t , приложенные к общей точке |
||||||||
|
||||||||||
(u0, v0) — точке пересечения кривых u = u0 и v = v0, по определению, перпенди- |
||||
|
Q = s |
· |
→− |
|
кулярны друг к другу. Но |
→− |
t = 0 |
(скалярное произведение ортогональных |
|
|
|
|||
векторов), см. рис.1.
Фиксируем теперь на поверхности точки P1(u1, v1) и P2(u2, v2), считая u1 < u2, и рассмотрим кривую, лежащую на поверхности и соединяющую точки P1 и P2,
задавая ее явно |
|
|
|
|
|
|
v = v(u) , |
u [u1, u2] , |
(1.11) |
||||
v1 |
= v(u1) , |
|
|
|||
(v2 |
= v(u2) , |
|
|
|
||
Тогда длина дуги этой кривой дается интегралом |
|
|||||
|
u2 |
|
|
|
|
|
I = Z |
|
|
|
|||
|
P + 2Qv0 + Rv02 |
du . |
(1.12) |
|||
u1 |
p |
|
|
|
||
Постановка некоторых . . .
Введение в вариационный метод Уравнение Эйлера–Лагранжа
Приложения
Обобщения Задачи на условный экстремум
Первое необходимое условие . . .
Семейства экстремалей
Динамика частиц
Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 9 из 197
Назад
Полный экран
Закрыть
Выход
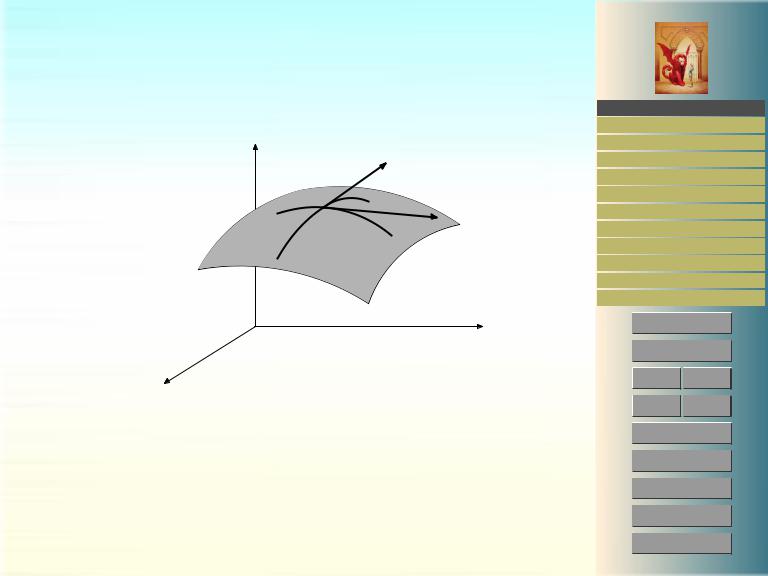
z |
−→ |
|
|
|
t |
→− s
v = v0
u = u0
y
x
Рис. 1: Криволинейные координаты на поверхности
Постановка некоторых . . .
Введение в вариационный метод
Уравнение Эйлера–Лагранжа Приложения Обобщения
Задачи на условный экстремум Первое необходимое условие . . .
Семейства экстремалей
Динамика частиц
Проблема минимума . . .
Существование минимума . . .
Лемма Гейне-Бореля
Веб – страница
Титульный лист
JJ II
J I
Страница 10 из 197
Назад
Полный экран
Закрыть
Выход
