Radiation Physics for Medical Physiscists - E.B. Podgorsak

5.3 Collision Stopping Power for Heavy Charged Particles

149

Since Z/A varies from substance to substance within quite a narrow range (it falls from 0.5 for low Z elements to 0.4 for high Z elements, with one notable exception of hydrogen for which Z/A ≈ 1), we note that the mass collision stopping power varies very slightly from substance to substance. This means that the energy losses of a given charged particle passing through layers of equal thickness in g/cm2 are about the same for all substances.

5.3.3 Minimum Energy Transfer

and Mean Ionization-Excitation Potential

For large impact parameters b the energy transfer ∆E(b), calculated from (5.14), may be smaller than the binding energy of the orbital electron or smaller than the minimum excitation potential of the given orbital electron. Thus, no energy transfer is possible for b > bmax where bmax corresponds to a minimum energy transfer ∆Emin, referred to as the mean ionizationexcitation potential I of the absorber atom. This potential depends only on the stopping medium but not on the type of the charged particle. It is always larger than the ionization potential of the atom since it accounts for all possible atomic ionizations as well as atomic excitations.

The mean ionization-excitation potential I corresponds to the minimum amount of energy ∆Emin that can be transferred on the average to an absorber atom in a Coulomb interaction between the charged particle and an orbital electron. Using (5.14), ∆Emin is written as

	e2		2	z2
	4πεo			meυ∞2 bmax2
∆Emin = 2					= I	(5.23)

√

showing that bmax 1/ I.

In general, the mean ionization-excitation potential I cannot be calculated from the atomic theory; however, it may be estimated from the following

empirical relationships:
I(in eV) ≈ 11.5 Z ,	(5.24)
or, to a better approximation,
I(in eV) = 9.1Z (1 + 1.9 Z−2/3) .	(5.25)

Some typical values for I are as follows (from the ICRU Report 37): hydrogen: 14.9 eV; carbon: 78 eV; aluminum: 167 eV; copper: 322 eV; water: 75 eV; air: 86 eV.

5.3.4 Maximum Energy Transfer

For small impact parameters b the energy transfer is governed by the maximum energy ∆Emax that can be transferred in a single head-on collision, as discussed in Sect. 4.3.2. Classically ∆Emax for a head-on collision between a

150 5 Interactions of Charged Particles with Matter

heavy charged particle M with kinetic energy EK and an electron with mass me is given by

	4meM		me	me M υ2
∆Emax =		EK ≈ 4		EK = 4		2 ∞	= 2meυ∞2 . (5.26)
	(me + M )2		M		M

Equation (5.26) shows that only a very small fraction (4me/M ) of the heavy charged particle kinetic energy can be transferred to an orbital electron in a single collision (note that M me).

The classical relationship between ∆Emax and the minimum impact parameter bmin that allows the maximum energy transfer from a heavy charged particle to an orbital electron is

		e2		2	z2
∆Emax = 2						= 2meυ∞2 ,			(5.27)
		4πεo			meυ∞2 bmin2
resulting in ∆Emax 1/bmin2				or bmin 1/√				.
							∆Emax

5.4 Mass Collision Stopping Power

The energy transfer ∆E(b) from a heavy charged particle to an orbital electron ranges from ∆Emin(bmax) = I to ∆Emax(bmin) = 2meυ∞2 ; i.e.,

I ≤ ∆E(b) ≤ 2meυ∞2 .											(5.28)
The ratio bmax/bmin, after combining (5.23) and (5.27), is given as
							2me	υ2
bmax				∆Emax
		=			=			∞	.		(5.29)
	bmin			∆Emin			I

•The classical mass collision stopping power of (5.22) for a heavy charged particle (Niels Bohr 1913) colliding with orbital electrons is then given with the following approximation:

2

Scol = 4π A NA

4πεo

meυ2

ln

I

∞ .

(5.30)

Z

e2

z2

2me

υ2

∞

•The non-relativistic quantum-mechanical expression for the mass stopping power of heavy charged particles was derived by Hans Bethe and Felix Bloch and it di ers from Bohr’s expression of (5.30) only in the occurrence of the power 1/2 in the Bohr’s logarithmic term. The Bethe-Bloch mass stopping power is

Z

e2

2

z2

2me

υ2

Scol = 4π

NA

ln

∞

.

(5.31)

A

4πεo

meυ∞2

I

5.4 Mass Collision Stopping Power

151

•Bethe’s relativistic quantum-mechanical expression for the mass collision stopping power of heavy charged particles accounts for relativistic e ects to get

Z

e2

2

z2

Scol = 4π

NA

A

4πεo

meυ∞2

ln

2

m

c2

,

e

+ ln β2 − ln(1 − β2) − β2

(5.32)

I

where β is the normalized incident particle velocity (β = υ/c) and the relativistic expression for ∆Emax of (4.38) is used.

–Two corrections were subsequently incorporated into Bethe’s expression for the mass collision stopping power:

–Correction CK/Z to account for non-participation of bound K-shell electrons in the slowing-down process. This correction reduces the collision stopping power but is only e ective at low kinetic energies of the charged particle.

–Polarization (density e ect) correction δ also lowers the collision stopping power. It is applied to condensed media (liquids and solids) for which the dipole distortion of the atoms near the track of the charged particle weakens the Coulomb force field experienced by the more distant atoms, thus decreasing their participation in the slowing down process.

–The polarization correction does not apply for gases, because in gases the atoms are spaced su ciently far apart to act independently of one another. The correction is also negligible for heavy charged particles at energies of interest in medical physics, but is significant for light charged particles (electrons and positrons).

•Incorporating the K-shell correction CK/Z and the polarization correction δ into Bethe’s relativistic quantum-mechanical expression results in the following relationship for the mass collision stopping power Scol for heavy charged particles:

Z

e2

2

z2

Scol = 4π

NA

A

4πεo

meυ∞2

2mec2

CK

− δ . (5.33)

ln

+ ln β2 − ln(1 − β2) − β2 −

I

Z

•Considering the various expressions stated above for the mass collision stopping power Scol of heavy charged particles, we can write Scol in general terms as follows:

	NA		e2		2	z2
Scol = 4π								(5.34)
							Bcol .
	A		4πεo			mec2(υ∞/c)2

152 5 Interactions of Charged Particles with Matter

Table 5.2. Expressions for the atomic stopping number Bcol for various energy ranges of heavy charged particle energy

Derivation

Bcol

Classical (Bohr)

Non-relativistic, quantum-mechanical (Bethe-Bloch)

Z ln		I	υ2
		2me
Z ln	2meυ2
		I

(5.36)

(5.37)

Relativistic,

Z ln

2mec2

2

− ln(1

− β

2

− β

2

quantum-mechanical

I

+ ln β

)

(5.38)

(Bethe)

Relativistic,

Z ln 2mec2

+ ln β2

− ln(1

− β

2

quantum-mechanical

2I

CK

)

(5.39)

with K-shell and

−β

−

− δ

Z

polarization correction

After inserting into (5.34) the appropriate values for the constants NA, e, εo, and mec2 and using β = υ∞/c we obtain the following expression for the mass collision stopping power Scol:

	Scol = 0.3070	MeV · cm2	z2	Bcol ,	(5.35)
		(gram − atom) Aβ2

where Bcol is called the atomic stopping number.

•The atomic stopping number Bcol is a function of the atomic number Z of the absorber (through the mean ionization-excitation potential I) and of the velocity of the charged particle. The form of the expression for Bcol also depends on the specific approach taken in its derivation, as indicated in Table 5.2.

The units of Scol in (5.35) are MeV · cm2/g; the constant in (5.35) has units of MeV · cm2/(gram-atom). Since the units of A are g/(gram-atom), incorporating an appropriate value for A into (5.35) results in proper units for Scol in MeV · cm2/g.

From the general expression for the mass collision stopping power given in (5.33) we note that the mass collision stopping power Scol for a heavy charged particle traversing an absorber does not depend on charged particle mass but depends upon:

1.Atomic number Z, atomic mass A, and mean ionization-excitation potential I in the form [Z/A and (− ln I)] of the absorber. As Z increases, Z/A and − ln I decrease resulting in a decrease of Scol.

5.4 Mass Collision Stopping Power

153

Fig. 5.4. Schematic representation of the shape of the collision stopping power curve as a function of the charged particle kinetic energy EK. Three regions are shown as the energy increases: (1) the rise of stopping power at low energies to reach a maximum at about 1500AI; (2) fall-o as 1/EK or 1/υ2 beyond the maximum to reach a minimum, and (3) slow relativistic rise at relativistic energies where υ ≈ c

2. Particle velocity υ. For increasing non-relativistic velocities Scol first increases, reaches a maximum, then decreases as 1/υ2, reaches a

broad minimum and	then slowly rises with the relativistic term
ln β2 − ln(1 − β2) − β2	as υ becomes relativistic and approaches c.

3.Particle charge ze. Scol increases as z2, i.e., a doubly charged particle experiences 4 times the collision stopping power of a singly charged particle of the same velocity υ moving through the same absorber.

As shown schematically in Fig. 5.4, the collision stopping power against EK goes through three distinct regions as the kinetic energy EK increases:

1.At low kinetic energies, Scol rises with energy and reaches a peak at 2.78IM/(4me), where M is the mass of the heavy charged particle and me the mass of the electron. The kinetic energy (EK)max at which the peak in Scol occurs can be estimated from the non-relativistic Bethe-Bloch equation [(5.31)] as follows:

Z

e2

2

z2

2

m

υ2

Scol = 4π

NA

ln

e

A

4πεo

meυ2

I

= const	1	ln	4		me	EK ,	(5.40)
	EK		I M

where

EK is the classical kinetic energy of the heavy charged particle; EK =

M υ2/2,

M is the mass of the heavy charged particle,

υis the velocity of the heavy charged particle.

154 5 Interactions of Charged Particles with Matter

(EK)max is determined by setting dScol/dEK|EK=(EK)max = 0 and solving for (EK)max

dEK

EK=EKmax

= 0 = − [(EK)max]2 ln I Me (EK)max +

[(EK)max]2

dScol

const

4 m

const

const

4 me

=

1 − ln

(EK)max . (5.41)

[(EK)max]2

I

M

Equation (5.41) results in the following expression for (EK)max:

(EK)max =

4 m

−1

e

e ≈ 1500 A I ,

(5.42)

I

M

where we use M ≈ MpA for the mass of the heavy charged particle, with Mp the proton mass and A the atomic mass number of the heavy charged particle; Mp/me ≈ 2000; and e ≈ 3.

2.Beyond the peak, Scol decreases as 1/υ2 or 1/EK of the charged particle until it reaches a broad minimum around 3Mabsorberc2, where Mabsorber is the rest mass of the absorber.

3.Beyond the broad minimum the mass collision stopping power Scol

rises slowly with kinetic energy EK as a result of the relativistic termsln β2 − ln(1 − β2) − β2

5.5 Collision Stopping Power for Light Charged Particles

Electron interactions (collisions) with orbital electrons of an absorber di er from those of heavy charged particles in three important aspects:

1.Relativistic e ects become important at relatively low kinetic energies.

2.Collisions with orbital electrons may result in large energy transfers of up to 50% of the incident electron kinetic energy. They may also result in elastic and inelastic electron scattering.

3.Collisions of electrons with nuclei of the absorber may result in bremsstrahlung production (radiative loss).

For electrons and positrons, energy transfers due to soft collisions are combined with those due to hard collisions using the Møller (for electrons) and Bhabba (for positrons) cross sections for free electrons. The complete mass collision stopping power for electrons and positrons, according to the ICRU Report 37, is

Z			mec2	ln	EK
Scol = 2πre2		NA				+ ln(1 + τ /2) + F ±(τ ) − δ , (5.43)
	A		β2		I
In (5.43) the function F −(τ ) is given for electrons as
F −(τ ) = (1 − β2) !1 + τ 2/8 − (2τ + 1) ln 2"							(5.44)

5.5 Collision Stopping Power for Light Charged Particles

155

Fig. 5.5. Mass collision stopping power for electrons in water, aluminum and lead against electron kinetic energy. The collision stopping power data are shown with solid curves; the radiative stopping power data of Fig. 5.2 are shown with dotted curves for comparison. Data were obtained from the NIST

The function F +(τ ) for positrons is given as
F +(τ ) = 2 ln 2 − (β2/12)
!23 + 14/(τ + 2) + 10/(τ + 2)2 + 4/(τ + 2)3"	, (5.45)

where

τis the electron or positron kinetic energy normalized to mec2, i.e., τ =

EK/mec2,

βis the electron or positron velocity normalized to c, i.e., β = υ/c.

Figure 5.5 shows mass collision stopping powers Scol for electrons in water, aluminum and lead with solid lines. For comparison, mass radiative stopping powers of Fig. 5.2 are shown with dotted lines. The data show that higher atomic number absorbers have lower Scol than lower atomic number absorbers at same electron energies. The dependence of Scol on stopping medium results from two factors in the stopping power expressions given by (5.33) and (5.43), both lowering Scol with an increasing Z of the stopping medium:

1.The factor Z/A makes Scol dependent on the number of electrons per unit mass of the absorber. Z/A is 1 for hydrogen; 0.5 for low Z absorbers; then gradually drops to 0.4 for high Z absorbers.

2.The − ln I term decreases Scol with increasing Z, since I increases almost linearly with increasing Z, as shown in (5.24) and (5.25).

156 5 Interactions of Charged Particles with Matter

5.6 Total Mass Stopping Power

Generally, the total mass stopping power Stot of charged particles is given by the sum of two components: the radiative stopping power Srad and the collision stopping power Scol, i.e.,

Stot = Srad + Scol .

(5.46)

For heavy charged particles the radiative stopping power is negligible (Srad ≈ 0), thus Stot = Scol

For light charged particles both components contribute to the total stopping power. Within a broad range of kinetic energies below 10 MeV collision (ionizational) losses are dominant (Scol > Srad); however, the situation is reversed at high kinetic energies where Srad > Scol.

The crossover between the two modes occurs at a critical kinetic energy (EK)crit where the two stopping powers are equal, i.e., Srad = Scol for a given absorber with atomic number Z. The critical kinetic energy (EK)crit can be

estimated from the following empirical relationship:
(EK)crit ≈	800 MeV	,	(5.47)
	Z

that for water, aluminum and lead amounts to 105 MeV, 61 MeV and10 MeV, respectively.

–For high Z absorbers the dominance of radiative losses over collision losses starts at lower kinetic energies than in low Z absorbers. However, even in high Z media such as lead and uranium (EK)crit is at 10 MeV, well in the relativistic region.

–The ratio of collision to radiative stopping power (Scol/Srad) at a given electron kinetic energy may be estimated from the following:

Scol	=	800 MeV	=	(EK)crit	.	(5.48)
Srad
		Z EK		EK

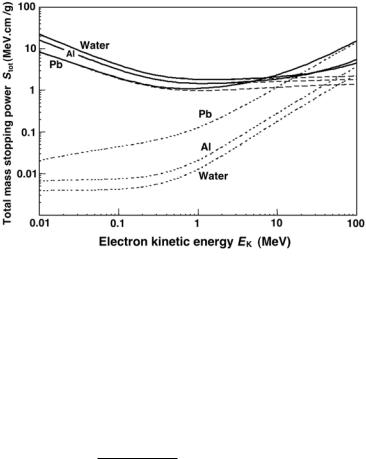
Figure 5.6 shows the total mass stopping power of electrons (solid curves) in water, aluminum and lead against the electron kinetic energy. For comparison the radiative and collision components of the total stopping power of Figs. 5.2 and 5.5 are also shown.

5.7 Bremsstrahlung (Radiation) Yield

The bremsstrahlung yield B(EKo) of a charged particle with initial kinetic energy EKo striking an absorber is defined as that fraction of the initial kinetic energy that is emitted as bremsstrahlung radiation through the slowing down process of the particle in the absorber.

5.7 Bremsstrahlung (Radiation) Yield

157

Fig. 5.6. Total mass stopping power Stot for electrons in water, aluminum and lead against the electron kinetic energy shown with solid curves. The mass collision and mass radiative stopping powers are shown with dotted curves for comparison. The total stopping power of a given material is the sum of the radiative and collision stopping powers. Data were obtained from the NIST

•For heavy charged particles B(EKo) ≈ 0.

•For light charged particles (electrons and positrons) the bremsstrahlung yield B(EKo) is determined from stopping power data as follows:

	EKo Srad(E)
	0			dE	1		EKo	Srad(E)
			Stot(E)
B(EKo) =					=				dE .	(5.49)
		EKo				EKo		Stot(E)
			dE				0
		0

•For positron interactions, annihilation-in-flight also produces photons; however, the e ect is generally ignored in calculation of the bremsstrahlung yield B(EKo).

•The energy Erad radiated per charged particle is

	Erad = EKo B(EKo) =	EKo	Stot(E) dE ,	(5.50)
		0
			Srad(E)
	while the energy Ecol lost through ionization per charged particle is
			Eo	Scol(E)
	Ecol = EKo − Erad = EKo [1 − B(EKo)] =
					dE . (5.51)
				Stot(E)

0

Kcol

158 5 Interactions of Charged Particles with Matter

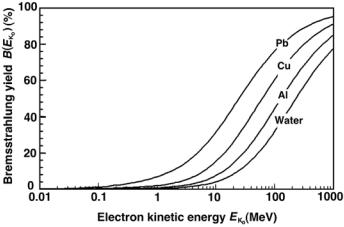
Fig. 5.7. Bremsstrahlung yield B(EKo) for electrons in water, aluminum, copper and lead against the incident electron kinetic energy. Data were obtained from the National Institute of Standards and Technology (NIST), Washington, D.C.

•Bremsstrahlung yield B(EKo) for water, aluminum, copper and lead is plotted against incident electron kinetic energy EKo in Fig. 5.7.

•In radiation dosimetry a quantity referred to as the radiative fraction g¯ is defined as the average fraction of the energy that is transferred from photons to electrons and positrons and subsequently lost by these particles to radiative processes that are predominantly bremsstrahlung interactions but can also include annihilation-in-flight interactions by positrons. The quantity g¯ appears in the following expressions:

	µ ab	=	µtr		(1 − g¯)	(5.52)
	ρ			ρ
and
Kcol = K(1 − g¯) ,						(5.53)

where

µab/ρ is the mass energy absorption coe cient for a photon beam, µtr/ρ is the mass energy transfer coe cient for a photon beam,

is the collision kerma,

K is the total kerma.

•The radiative fraction g¯ is the average value of B(EKi ) for all electrons and positrons of various initial energies EKi present in the spectrum of light charged particles produced in a medium by either monoenergetic photons or a photon spectrum.

•B(EKo) is the bremsstrahlung yield defined for monoenergetic electrons with initial energy EKo, while g¯ is the radiative fraction calculated for a spectrum of electrons and positrons produced in the medium by photons.