Radiation Physics for Medical Physiscists - E.B. Podgorsak

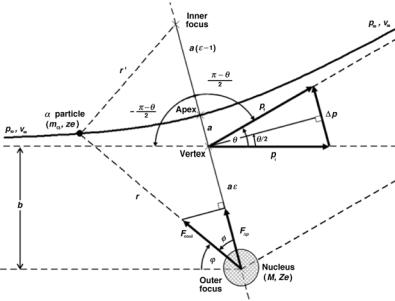
2.2 Rutherford Atom and Rutherford Scattering

49

Fig. 2.3. Schematic diagram for scattering of an α particle on a nucleus: θ is the scattering angle; b the impact parameter; ∆p the change in α-particle momentum; υ∞ the initial velocity of the α particle; and p∞ the initial momentum of the α particle. The trajectory of the α particle is a hyperbola as a result of the repulsive Coulomb interaction between the α particle and the nucleus

Since the component of the force Fcoul in the direction of the momentum transfer is F∆p = Fcoul cos φ, the momentum transfer (impulse) ∆p may be written as the time integral of the force component F∆p, i.e.,

∞

∞

	∆p =	F∆pdt =			Fcoul cos φ dφ
	−∞			−∞
			π−θ
		zZe2	2	cos φ dt
	=							(2.10)
							dφ ,
		4πεo		r2		dφ

−π−θ

2

where φ is the angle between the radius vector r and the bisector, as also shown in Fig. 2.3.

Using the conservation of angular momentum L

L = m υ	∞	b = m	ω r2 ,	(2.11)
α		α

50 2 Rutherford–Bohr Atomic Model

where

mα is the mass of the α particle,

bis the impact parameter,

ris the radius vector between the α particle and the nucleus,

υ∞	is the initial and final α-particle velocity before and after the interac-
	tion,
ω	is the angular frequency equal to dφ/dt,
we can now rewrite (2.10) in a simple form
						π−θ
	zZe2 1					2		zZe2	1
											{sin φ}−(π−θ)/2
	∆p = 4πεo υ∞b						cos φdφ = 4πεo		υ∞b
											+(π−θ)/2

−π−θ

2

= 2	zZe2	1			cos	θ		(2.12)
							.
	4πεo		υ∞b
					2

With the help of the momentum vector diagram, also given in Fig. 2.3, the momentum transfer ∆p may also be written as

∆p = 2p∞ sin	θ		= 2mαυ∞ sin	θ		(2.13)
					.
	2			2

Combining (2.12) and (2.13) we obtain the following expressions for the impact parameter b

zZe2

θ

1 zZe2

1

θ

1

θ

b =

cot

=

cot

=

D

cot

, (2.14)

EK

2

4πεomαυ2

2

2 4πεo

2

2

α−N

∞

with the use of:

1.the classical relationship for the kinetic energy of the α particle (EK = mαυ∞2 /2), since υ∞ c,

2.the definition of Dα−N as the distance of closest approach between the α particle and the nucleus in a “direct-hit” head-on collision for which the impact parameter b = 0, the scattering angle θ = π, and Dα−N =

zZe2/(4πεoEK).

Hyperbolic Trajectory

Equations for the hyperbolic trajectory of an α particle interacting with a nucleus can be derived from the diagram given in Fig. 2.3 and the simple rule governing the hyperbola

r − r = 2a ,

(2.15)

where

a is the distance between the apex and the vertex of the hyperbola,

ris the distance between the point of interest on the hyperbola and the outer focus,

2.2 Rutherford Atom and Rutherford Scattering

51

r is the distance between the point of interest on the hyperbola and the inner focus.

The parameters of the hyperbola such as a, r, and r are defined in Fig. 2.3 and the locations of the inner focus, outer focus, apex and vertex are also indicated in Fig. 2.3. Solving (2.15) for r and squaring the result, we get the following expression for (r )2

(r )2 = r2 − 4ar + 4a2 .

(2.16)

Using the law of cosines in conjunction with Fig. 2.3, we express (r )2 as

(r )2 = r2 − 4aεr cos φ + 4a2ε2 ,

(2.17)

where ε is the eccentricity of the hyperbola. Subtracting (2.17) from (2.16) and solving for r(φ), we now obtain the following general equation for the hyperbolic trajectory of the α particle

r(φ) =	a(ε2 − 1)	.	(2.18)
	ε cos φ − 1

Three separate special conditions are of interest with regard to (2.18):

1.r = ∞ (for determining the eccentricity ε)

2.φ = 0 (for determining the general distance of closest approach Ra−N)

3.θ = π (for determining the distance of closest approach in a direct hit

that results in the shortest distance of closest approach defined as Dα−N)

For r = ∞ the angle φ equals to (π − θ)/2 and the denominator in (2.18) [ε cos((π − θ)/2) − 1] must equal zero, resulting in the following relationship for the eccentricity ε

	ε cos	π − θ	= ε sin	θ		= 1 or ε =	1		.	(2.19)
		2		2			sin	θ
								2

The distance of closest approach Rα−N between the α particle and the nucleus in a non-direct hit collision (θ < π and φ = 0) is given as

R	α−N	= r(φ = 0) =	a(ε2 − 1)				= a(1 + ε)
					ε − 1
				θ		−1
		= a 1 + sin				.	(2.20)
				2

The distance of closest approach in a direct-hit collision (θ = π) can now be written as

Dα−N = Rα−N(θ = π) = 2a ,

(2.21)

from where it follows that a, the distance between the apex and the vertex of the hyperbola, is equal to Dα−N/2.

52	2 Rutherford–Bohr Atomic Model
Hyperbola in Polar Coordinates
In polar coordinates						(r, ϕ) the hyperbolic α-particle trajectory may be ex-
pressed as
	1		1				a
			=		sin ϕ +			(cos ϕ − 1) ,	(2.22)
		r		b			b2

with parameters a, b, and ϕ defined in Fig. 2.3. Note that ϕ and φ are di erent angles and that the following relationship for angles ϕ, φ, and θ applies

π − θ

ϕ + φ =		.	(2.23)

2

It can be shown that the expressions of (2.18) and (2.22) for a hyperbola are equivalent.

2.2.3 Di erential Cross-Section for Rutherford Scattering

The di erential cross-section dσRuth/dΩ for Rutherford scattering into a solid angle dΩ = 2π sin θ dθ that corresponds to an angular aperture between θ and θ + dθ (equivalent to impact parameters between b and b − db), assuming the azimuthal distribution to be isotopic, is the area of a ring with mean radius b and width db

dσRuth = 2π b db = 2π sin θ

b

db

dθ .

(2.24)

sin θ

dθ

Recognizing that

dΩ = 2π sin θ dθ ,

(2.25)

expressing sin θ as

sin θ = 2 sin

θ

cos

θ

,

(2.26)

2

2

and using (2.14) for the impact parameter b to determine |db/dθ| as

Dα−N

1

db

=

(2.27)

dθ

4

sin2(θ/2)

,

we obtain

the

following expression for dσRuth/dΩ, the di erential Rutherford

cross section

dσRuth

Dα−N

2

1

=

.

(2.28)

dΩ

4

sin4 θ2

At small scattering angles θ, where sin(θ/2) ≈ θ/2, (2.28) may be approximated as

	dσRuth	=	Dα2 −N	.	(2.29)
	dΩ
			θ4

Since most of the Rutherford scattering occurs for θ 1 rad and even at θ = π/2 the small angle result is within 30% of the Rutherford general expression, it is reasonable to use the small angle approximation of (2.29) at all angles for which the unscreened point-Coulomb field expression is valid.

2.2 Rutherford Atom and Rutherford Scattering

53

2.2.4 Minimum and Maximum Scattering Angles

Departures from the point Coulomb field approximation appear for large and small angles θ, corresponding to small and large impact parameters b, respectively.

At large b (i.e., at small θ) the screening e ects of the atomic orbital electrons cause the potential felt by the α particle to fall o more rapidly than the 1/r Coulomb point-source potential. It is convenient to account for electron screening of the nuclear potential with the Thomas-Fermi statistical model of the atom in which the Thomas-Fermi atomic potential is given as follows:

VTF(r) ≈	Ze2 1				(2.30)
				e−r/aTF .
	4πεo		r
In (2.30) aTF is the Thomas-Fermi atomic radius expressed as
aTF ≈ 1.4aoZ−1/3 ,					(2.31)

representing a fixed fraction of all atomic electrons or, more loosely, the radius

˚

of the atomic electron cloud that screens the nucleus (ao = 0.5292 A is the Bohr radius, discussed in Sect. 2.3). This implies that with a decreasing scattering angle θ the scattering cross-section will flatten o at small angles θ to a finite value at θ = 0 rather than increasing as θ−4 and exhibiting a singularity at θ = 0.

The small angle result of (2.29) may then in general be written as

dσRuth		D2
	≈	α−N	(2.32)
dΩ		(θ2 + θmin2 )2

In contrast to (2.29) which is singular at θ = 0 the relationship in (2.32) provides a finite value at θ = 0 equal to

dσRuth		=	D2		(2.33)
dΩ	θ=0			θmin4

For small angular deflections θ where ∆p p and θ ≈ 0 we can write

	∆p		2zZe2		D
θ ≈		=		=	α−N	(2.34)
	p∞		4πεov∞b p∞		b

using (2.2), (2.12), and (2.13)

Substituting aTF, the Thomas-Fermi radius of the atom, for b into (2.34) we estimate θmin as

θmin = Dα−N/aTF ,

(2.35)

while the quantum-mechanical result is

54	2 Rutherford–Bohr Atomic Model
				3
	θmin =		=		c √Z				(2.36)
		paTF		1.4ao
					EK(EK + 2Eo)

using the expressions for p and aTF given by (1.50) and (2.31), respectively. At relatively large scattering angles θ the di erential Rutherford cross section dσRuth/dΩ is smaller than that predicted by (2.28) because of the fi- nite size of the nucleus. Approximating the charge distribution of the atomic nucleus by a volume distribution inside a sphere of radius R results in the following electrostatic potentials V (r) for regions inside and outside the nu-

cleus

V (r) =

zZe2

3

−

1 r2

4πεoR

2

2

R2

V (r) =

3 zZe2

8 πεoR

V (r) =

zZe2

4πεoR

V (r) =

zZe2

4πεor

for r < R,	(2.37)
for r = 0 ,	(2.38)
for r = R ,	(2.39)
for r > R .	(2.40)

The scattering is confined to angles smaller than θmax = λ/(2πR) where λ is the de Broglie wavelength of the incident particle. The maximum scattering angle θmax is then approximated as follows using the expressions for p of (1.50) and R: of (2.1)

θmax =		=			c				.	(2.41)
	pR		EK(EK + 2Eo) Ro .√A
			3

Using (2.36) and (2.41) we obtain the following expression for θmax/θmin

	θmax	=	aTF	=	1.4ao			,	(2.42)
					3
	θmin R
					Ro √ZA

ranging from 5 × 104 for low atomic number elements to 2 × 103 for high atomic number elements. Thus, we may conclude that θmax/θmin 1 for all elements.

2.2.5 Total Rutherford Scattering Cross-Section

The total Rutherford scattering cross section can be approximated by using the small angle approximation and integrating (2.32) over the complete solid angle to obtain

	2.2	Rutherford Atom and Rutherford Scattering	55
σRuth =	dσRuth	dΩ =
	dΩ

= 2π	θmax		dΩ		sin θ dθ ≈ 2π Dα2		−N
	0
		dσRuth
			θmax	d(θ2 + θmin2 )
	2		0
= π Dα−N						=
				(θ2 + θmin2 )2

θmax	(θ2 + θmin2	)2 =
0
	θ dθ

1

= π Dα2 −N

1

−

=

θ2

θ2

+ θ2

min

max

min

= π Dα2 −N

1

1

(2.43)

θ2

1

−

1 + (θ2

/θ2

)

.

min

max

min

In each Rutherford collision the angular deflections obey the Rutherford’s expression with cut-o s at θmin and θmax given by (2.36) and (2.41), respectively. The typical value for /p in the two expressions can be estimated for

α particles with a typical kinetic energy of 5.5 MeV as follows:
		=	c		≈	200 MeV · fm	= 1 fm .	(2.44)
	p		mαc2(υ/c)			4 × 103 MeV 5 × 10−2

Inserting the value for /p into (2.36) and (2.41) for a typical α-particle kinetic energy EK of 5.5 MeV combined with appropriate values for aTF and R results in the following values for θmin and θmax in the gold atom

θmin ≈					≈		1 fm			= 5 × 10−5 rad	(2.45)
	paTF						2 × 104 fm
						1 fm
θmax ≈			≈					= 10−1 rad .			(2.46)
	pR					10 fm

Rutherford’s condition stipulating that θmin θmax 1 is thus satisfied and, since also θmax/θmin 1, the total cross section for Rutherford’s scattering given in (2.43) can be simplified, after inserting (2.2) and (2.36), to read

		π D2			2zZe2		2
			2			.
		α−N
	σRuth ≈	θmin2	= πaTF		4πεo υ			(2.47)
The parameters of (2.47) are as follows:
aTF	is the Thomas-Fermi atomic radius,
Z	is the atomic number of the absorber foil,
z	is the atomic number of the α particle,
υ	is the velocity of the α particle,
Dα−N	is the distance of closest approach between the α particle and nucleus
	in a direct-hit collision (b = 0).

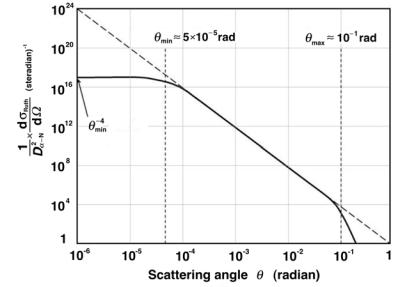
The di erential Rutherford scattering cross section of (2.32) is plotted in Fig. 2.4 in the form (1/Dα2 −N)(dRRuth/dΩ) against the scattering angle θ for

56 2 Rutherford–Bohr Atomic Model

Fig. 2.4. Di erential Rutherford scattering cross section [(1/Dα2 −N)×(dσRuth/dΩ)] plotted against the scattering angle θ for 5.5 MeV α particles interacting with gold. The minimum and maximum scattering angles θmin = 5 × 10−5 rad and θmax = 10−1 rad, respectively, are identified. For θ → 0 the value of the ordinate approaches (1/θmin4 ) ≈ 1.6 × 1017 (rad)−4

scattering of 5.5-MeV α particles [θmin = 5 × 10−5 rad, as given in (2.45) and θmax = 10−1 rad, as given in (2.46)] on gold nuclei.

The solid curve of Fig. 2.4 represents the di erential Rutherford scattering cross section and contains the following components:

1.For θmin < θ < θmax the simple di erential Rutherford scattering expression given by (2.29) applies resulting in a straight line on the log-log plot in Fig. 2.4.

2.For θ < θmin (2.32) applies since it accounts for the screening of the

nuclear potential by orbital electrons and provides a finite value of 1/θmin4 = 1.6 × 1017 rad−4 for θ = 0 in Fig. 2.4.

3.For θ > θmax the finite size of the nuclear potential must be considered and this lowers the value of the di erential cross section from the value predicted by the simple Rutherford result of (2.29).

2.2.6 Mean Square Scattering Angle for Single Rutherford Scattering

Rutherford scattering is confined to very small angles and for energetic α particles θmax 1 rad. An α particle traversing a gold foil will undergo

2.2 Rutherford Atom and Rutherford Scattering

57

a large number of small angle θ scatterings and emerge from the foil with a small cumulative angle Θ that represents a statistical superposition of a large number of small angle deflections.

Large angle scattering events, on the other hand, are rare and a given α particle will undergo at most only one such rare scattering event while traversing the gold foil. As discussed in Sect. 2.1.2, Geiger and Marsden found that only about 1 in 104 α particles traverses the 1 m thick gold foil with a scattering angle Θ exceeding 90◦. The range of Rutherford angular scattering is thus divided into two distinct regions:

1.Single scattering events with large angle θ.

2.Multiple scattering events resulting in a small cumulative angle Θ.

In the multiple-scatter region, the mean square angle for single scattering θ2 is

			θ2 dσRuth dΩ				θ2 dσRuth dΩ
θ2 =				dΩ	=		dΩ	.	(2.48)
				dσRuth
				dΩ dΩ			σRuth

The denominator in (2.48) is the total Rutherford scattering cross section σRuth given in (2.47). It is proportional to the square of the distance of closest approach (Dα−N)2 and inversely proportional to θmin2 .

The integral in the numerator of (2.48) is in the small angle approximation (sin θ ≈ θ) calculated as follows:

θ2

dΩ

dΩ = 2πDα2

−N

θmax

(θ2

+ θmin2 )2

0

dσRuth

θ2 sin θdθ

θmax

θ3dθ

≈ 2πDα2

0

−N

(θ2 + θmin2 )2

θmax

)d(θ2 + θmin2

2

0

(θ2 + θmin2

)

= πDα−N

(θ2 + θmin2 )2

2

θmax θmin2 d(θ2 + θmin2 )

−πDα−N

0

(θ2 + θmin2 )2

2

2

2

θmin2

θmax

= πDα−N ln(θ

+ θmin) +

0

θ2 + θmin2

−

θmin2

θmax2

+ θmin2 −

= πD2

N

ln

1 +

θmax2

+

θmin2

1 .

(2.49)

α

The mean square angle θ2 of (2.48) for a single scattering event, after incorporating the Rutherford total scattering cross section given in (2.47), is then

58 2 Rutherford–Bohr Atomic Model

given by the following relationship:

= θmin2

ln

1 +

θmax2

−

θmin2 θmax2

θ2

θmin2

θmin2 + θmax2

−1

= θmin2

θ2

−

1

1

1 +

+

.

(2.50)

θmin2

θmin2

θmax2

ln

max

The expression in (2.50) can be simplified using the Rutherford scattering condition stipulating that θmin θmax 1 to obtain

θ2 ≈ 2 θmin2	ln	θmax	(2.51)
		θmin .

2.2.7 Mean Square Scattering Angle for Multiple Rutherford Scattering

Since the successive scattering collisions are independent events, the centrallimit theorem of statistics (see Sect. 4.4.6) shows that for a large number n > 20 of such collisions, the distribution in angle will be Gaussian around the

forward direction [see (2.7)] with a cumulative mean square angle Θ2 related

to the mean square angle θ2 for a single scattering event given in (2.51).

The cumulative mean square angle Θ2 and the mean square angle θ2 for a single scattering event are related as follows:

Θ2 = nθ2 ,

where n, the number of scattering events, is given as follows:

	Na		NA		NA D2
n =		σRutht = ρ		σRutht = πρ		α−N	t .
	V		A		A θmin2

In (2.53) the parameters are as follows:

(2.52)

(2.53)

σRuth is the total Rutherford cross-section given by (2.47), Na/V is the number of atoms per volume equal to ρNA/A, ρ is the density of the foil material,

t is the thickness of the foil,

Ais the atomic mass number,

NA is the Avogadro’s number (NA = 6.023 × 1023 atom/gramatom), Dα−N is the distance of closest approach between the α particle and the

nucleus in a direct hit interaction where b = 0 [see (2.2)], θmin is the cut-o angle defined in (2.36).

The mean square angle Θ2 of the Gaussian distribution after combining (2.51), (2.52) and (2.53) is then given by

		= 2πρ	NA	tD2	ln	θmax	,	(2.54)
	Θ2
			A α−N			θmin

indicating that the mean square angle Θ2 for multiple Rutherford scattering increases linearly with the foil thickness t. Inserting the expressions for