Краткие теоретические сведения и образец выполнения заданий контрольной работы № 4 Числовой ряд и его сходимость. Необходимое условие сходимости ряда

Числовым рядом называется выражение вида

,

u_k=f (k) называется общим членом ряда.

Сумма конечного числа n первых членов ряда называется п-ой частичной суммой ряда:

.

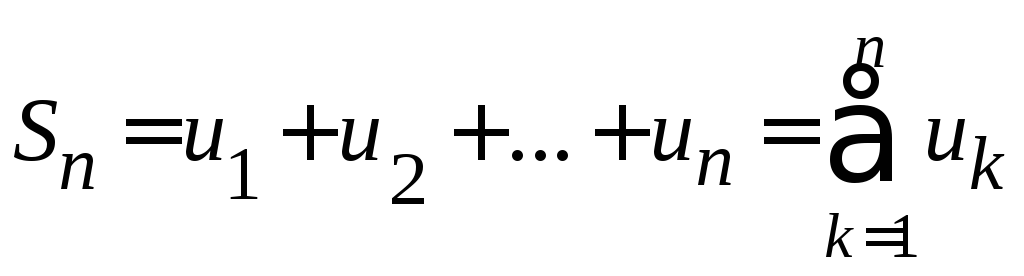Ряд u_n+1+u_n+2+…=называетсяп-м остатком ряда.

Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм: . ЧислоS называется суммой ряда. При этом пишут = S. Если предел частичных сумм равен бесконечности, т.е. , или не существует, то ряд называетсярасходящимся.

Рассмотрим ряд из членов геометрической прогрессии (геометрический ряд):

a+aq+aq²+…+aqⁿ+…a·qⁿ.

Сумма первых п членов геометрической прогрессии вычисляется по формуле S_n=a+aq+aq²+…+aq^n-1=, если . Если<1, то, т.е. ряд сходится и его сумма S=aq^п=. Если >1,то ряд расходится:в случаеи не существует в случае.

Итак, геометрический ряд aqⁿ сходится тогда и только тогда, когда <1, и его суммаS=.

Если ряд сходится, то егоп-й член при является бесконечно малой величиной, т.е.. Это необходимое условие сходимости ряда. Если же, то ряд расходится (достаточный признак расходимости ряда).

Пример 1. Записать общий член ряда и доказать, что этот ряд расходится.

Решение. Рассмотрим числители членов ряда 1,3,5,7,…; каждый следующий больше предыдущего на одно и тоже число 2, т.е. они образуют арифметическую прогрессию с первым членом а₁=1 и разностью прогрессии d=2. Используем формулу общего члена арифметической прогрессии

a_n=a₁+d(n-1).

Получим, что числители членов ряда меняются по формуле

1+2 (п-1)=1+2n-2=2n-1.

Знаменатели 5,10,15,20,… образуют арифметическую прогрессию с а₁=5 и d=5, поэтому меняются по формуле

5+5 (п-1)=5+5n-5=5n.

Поэтому общий член ряда выражается формулой .

Найдем его предел:

.

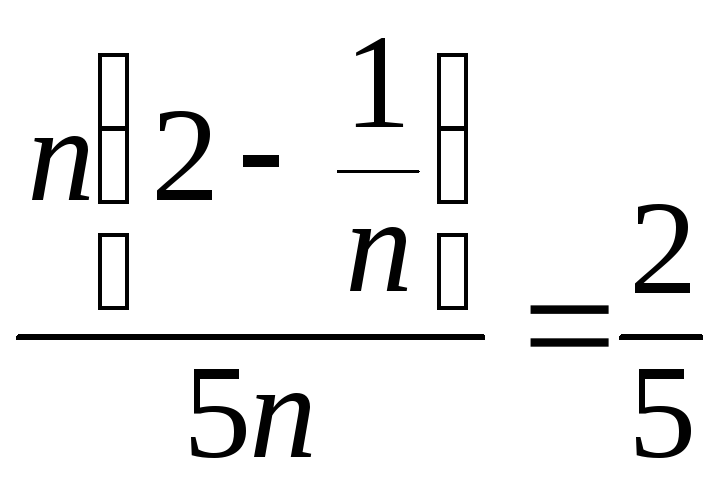Итак, , следовательно, согласно достаточному признаку расходимости ряда, данный ряд расходится.

Положительные ряды

Числовой ряд называютположительным, если все члены ряда неотрицательны, т.е. при любом n.

Теорема (критерий сходимости положительного ряда). Для того чтобы положительный числовой ряд сходился, необходимо и достаточно, чтобы его п-я частичная сумма была ограничена сверху, т.е. S_nM.

Для исследования сходимости применяют достаточные признаки. Среди них часто используют признаки сравнения, Даламбера, радикальный и интегральный признаки Коши.

Признаки сравнения

Теорема (1-й признак сравнения). Пусть даны два положительных ряда: ии пусть для всехп начиная с некоторого номера, выполняется . Тогда

1. если ряд 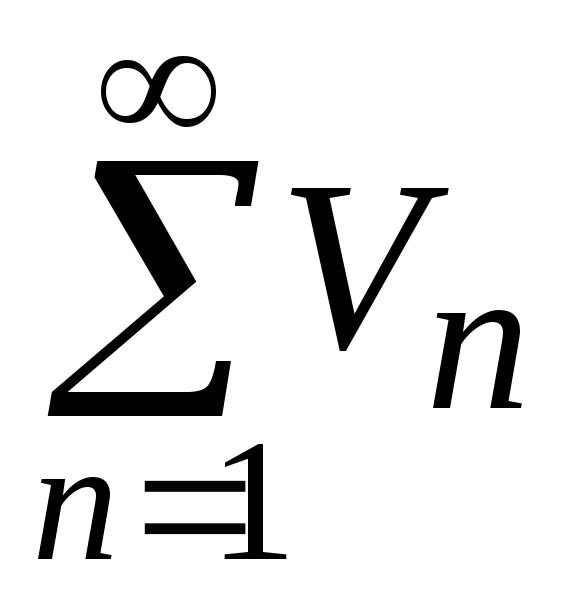сходится, то ряд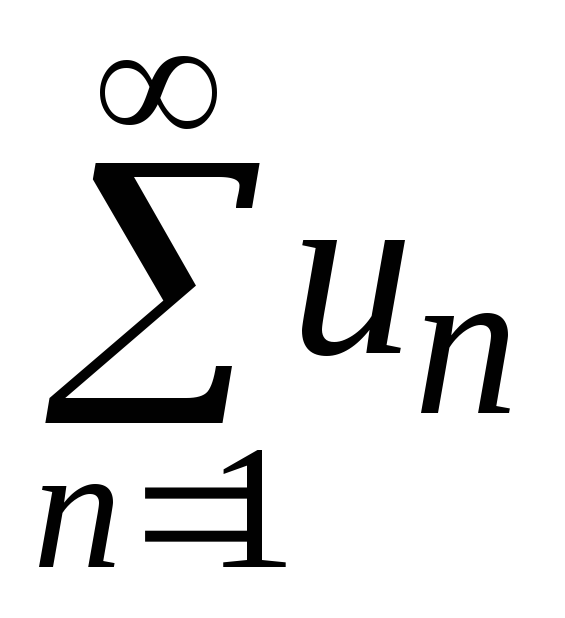также сходится;

2. если ряд 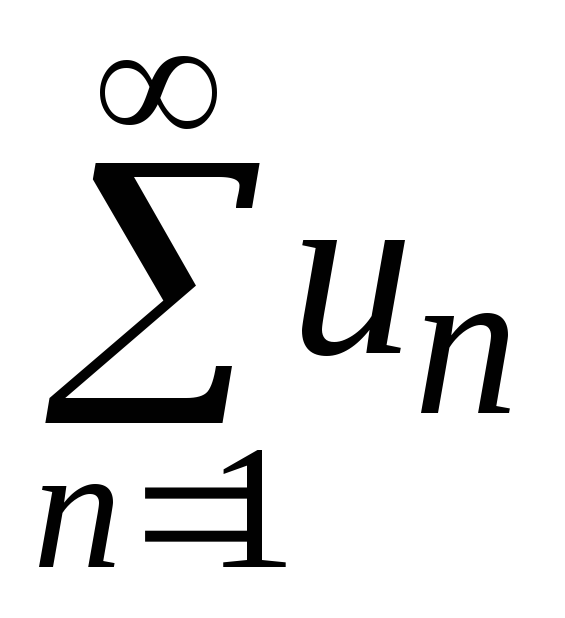расходится, то ряд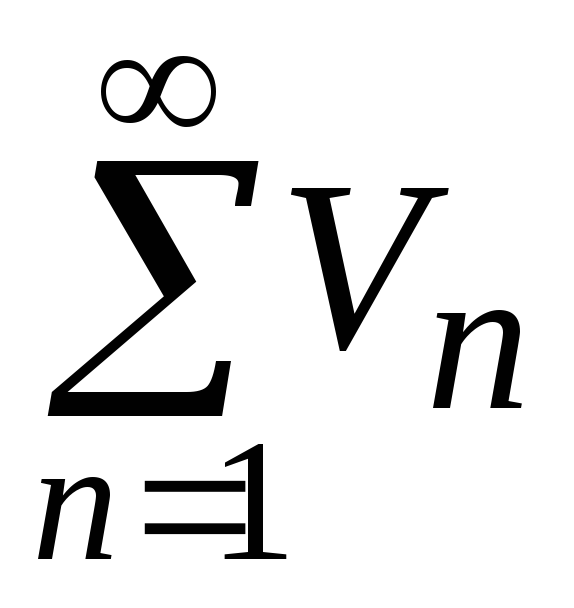также расходится.

Теорема (2-й признак сравнения). Если существует конечный, отличный от нуля предел 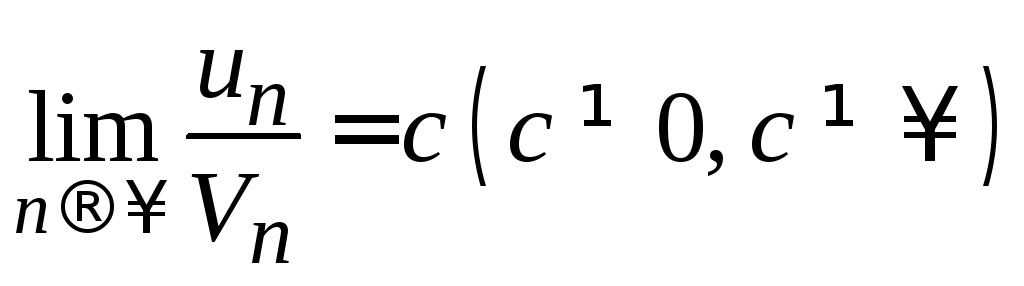, то ряды эквивалентны в смысле сходимости, т.е. оба ряда сходятся или расходятся одновременно.

Для сравнения используются эталонные ряды:

1. геометрический ряд 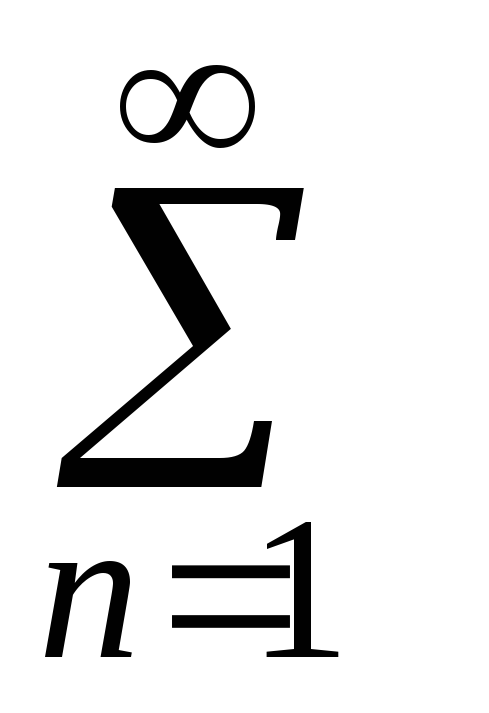aq^п, который сходится при <1 и расходится при1;

б) обобщенный гармонический ряд , который сходится прир>1 и расходится при р1. В случае р=1 ряд называют гармоническим.

При выборе рядов для сравнения полезно помнить следующие специальные пределы:

; ;;

; .

Удобно также использовать неравенства:

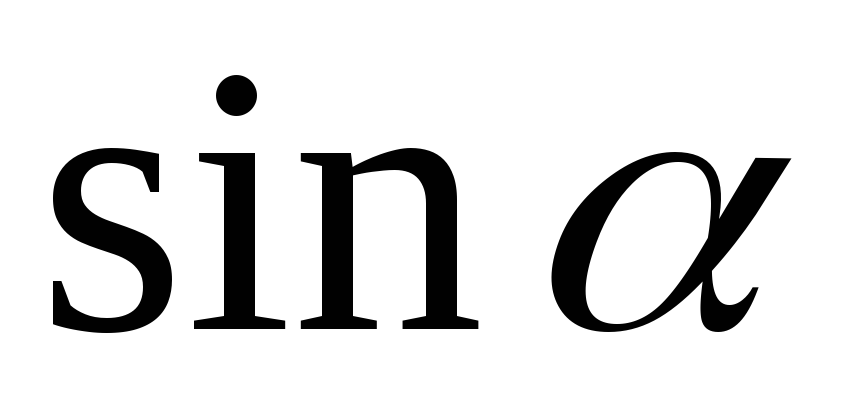1. <<, если 0<<;

2. ; ;

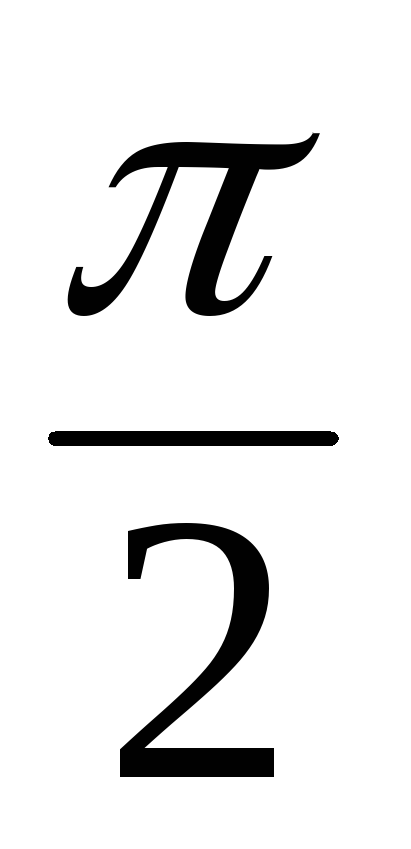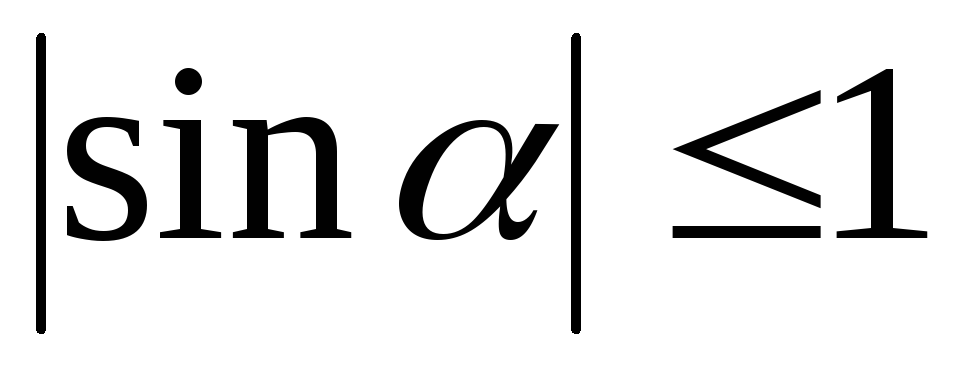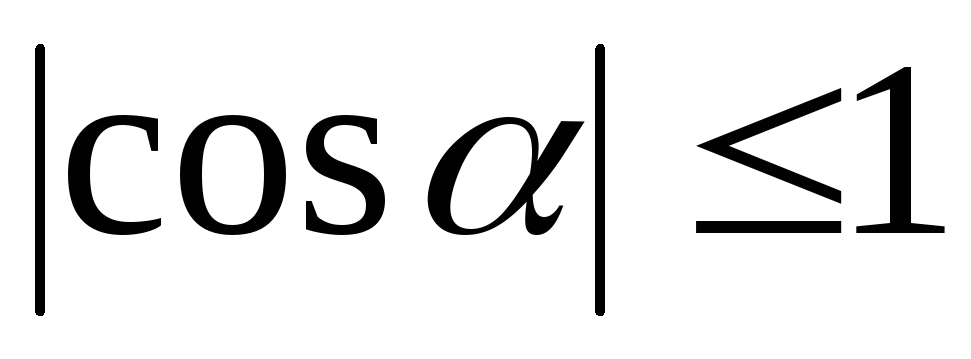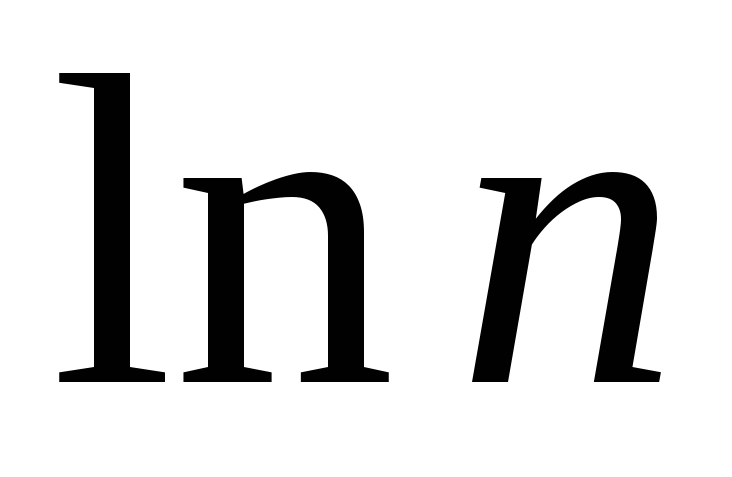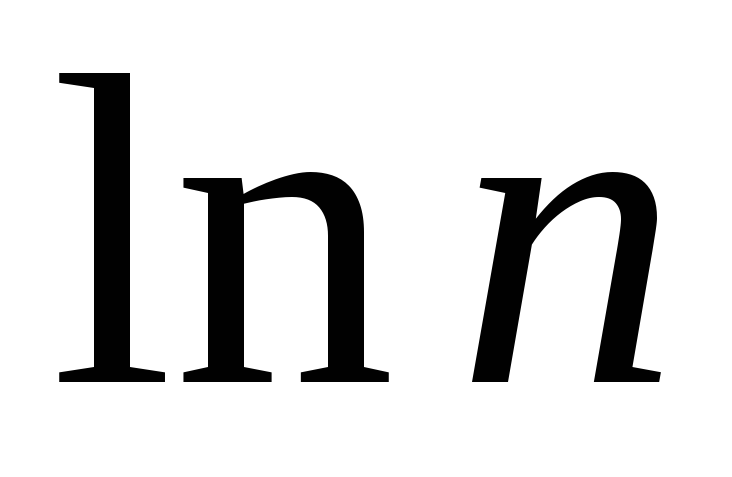3. <для всех натуральныхп и >1 при.

Пример 2. Исследовать на сходимость ряды:

а) ; б); в).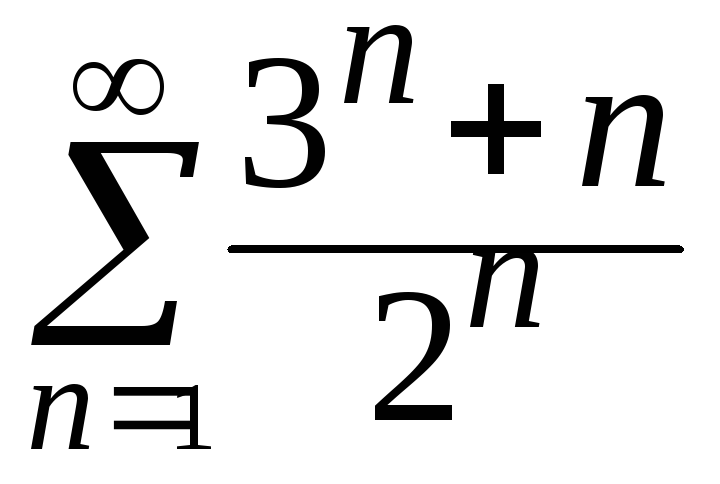

Решение.

а) Для сравнения возьмем ряд , который сходится как обобщенный гармонический ряд (р=2>1).

Поскольку прип > 1, то по первому признаку сравнения исходный ряд также сходится.

б) Для сравнения возьмем ряд 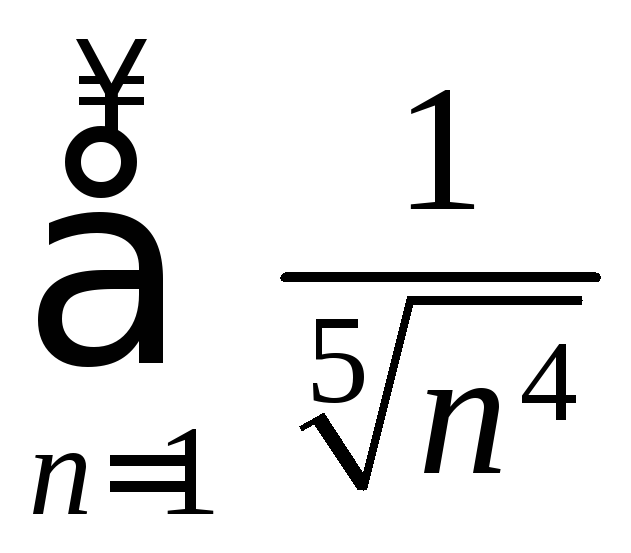, который расходится как обобщенный гармонический ряд (р=<1).

Применим 2-й признак сравнения:

=

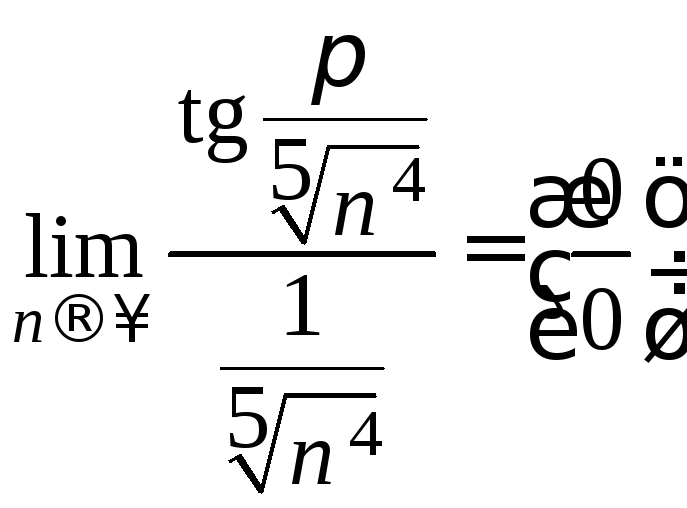Следовательно, ряды эквивалентны в смысле сходимости, и значит, исходный ряд также расходится.

в) Для сравнения возьмем ряд , который расходится как геометрический ряд (q=>1).

Поскольку u_n => для всех п , то по первому признаку сравнения исходный ряд также расходится.

Признак Даламбера. Пусть для положительного ряда существует конечный пределD =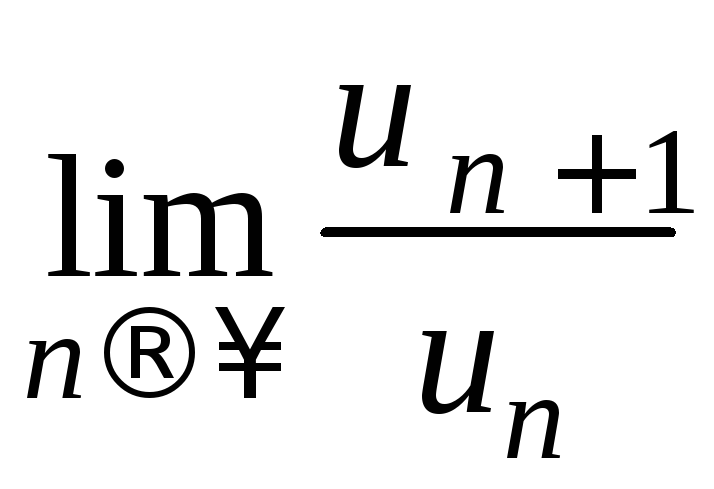. Тогда, еслиD<1, то ряд сходится, если D >1 – ряд расходится, при D=1 – ничего определенного о сходимости или расходимости ряда утверждать нельзя.

Признак Даламбера используется, если в записи п-го члена ряда присутствует либо а^п наряду с , либо факториалп!.

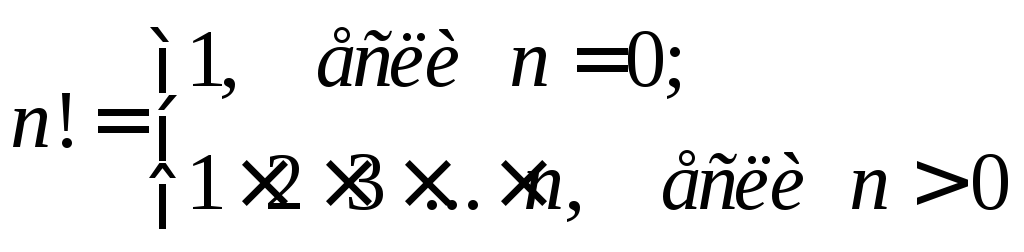(читается «эн-факториал»).

Пример 3. Исследовать сходимость ряда

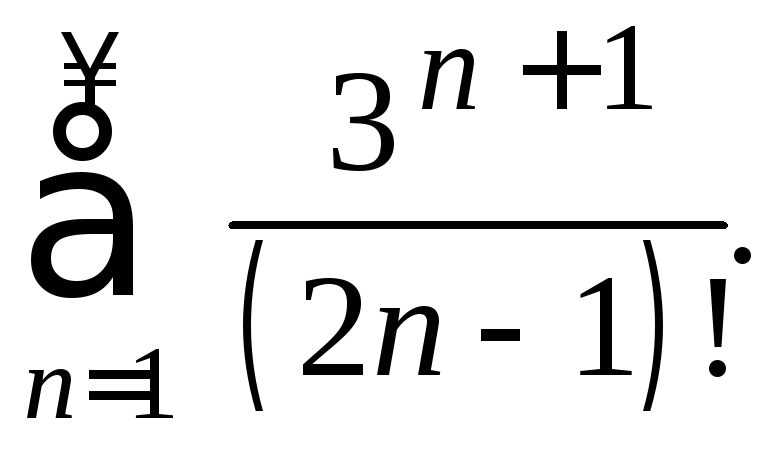
Решение. Применим признак Даламбера. Общий член ряда , (п+1)-й член ряда

Вычисляя предел D=, получаем:

D=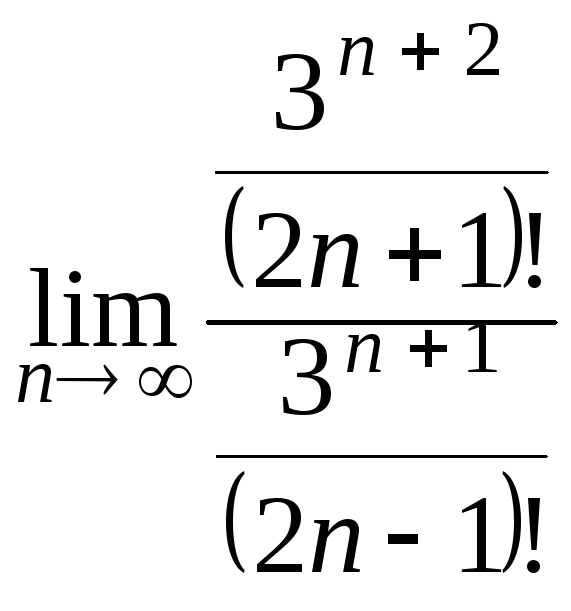==3

Согласно признаку Даламбера ряд сходится.

Радикальный признак Коши. Пусть для положительного ряда существует конечный пределК=. Тогда, еслиК<1, то ряд сходится, если К>1 – ряд расходится; при К=1 – ничего определенного о сходимости или расходимости ряда утверждать нельзя, нужно применить другой признак.

Пример 4. Исследовать сходимость ряда .

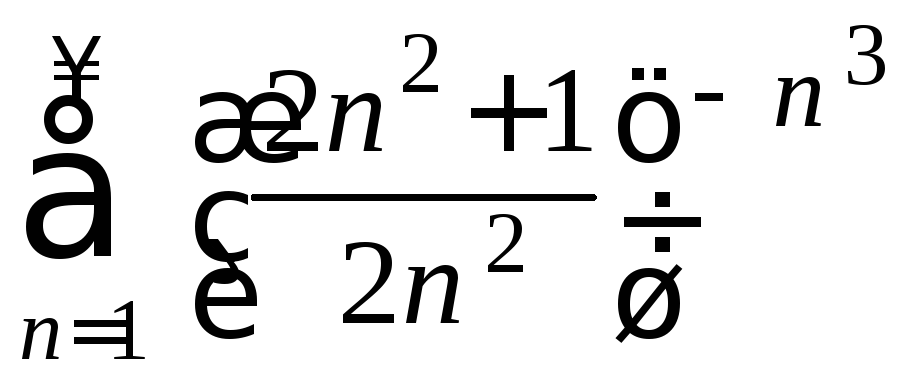Решение. Используем радикальный признак Коши. Общий член ряда . НайдемК=:

К====

= =.

Следовательно, исследуемый ряд сходится.

Замечание. При решении использован второй замечательный предел