1-й сем-ДМ-слайды-ДГТУ / Высказывания1-5

Основные понятия математической логики. Высказывания. Истинность высказываний. Операции над высказываниями: дизъюнкция, конъюнкция, импликация, эквивалентность. Таблицы истинности, свойства.

Высказывание – любое предложение, утверждающее что-либо о чем-либо, при этом можно сказать истинно оно или ложно в данном месте в данное время.

Логические значения истина-«true» и ложь-«false».

Примеры:

1. Ростов стоит на Дону

2. Москва – деревня в Ростовской области

3. Число 6 делится на 2 и 3

1 и 3 – true

2 – false

Высказывания, полученные из элементарных, с помощью связок «не», «и», «или», «если …, то», «тогда и только тогда» - сложные или составные.

Ни одно высказывание не может быть одновременно истинным и ложным.

Имея, x,y,z,…,a,b,c – высказывания;

И, 1, true – истинна;

Л, 0, false – ложь.

Если a – истинно, то a=1; если ложно, a=0.

1. Отрицание

Отрицание истинно, если x – ложно и наоборот.

X, не X, или «неверно, то X»

Таблица истинности:

X	X
1	0
0	1

X – двойное отрицание.

X=X

2. Конъюнкция (логическое умножение)

Конъюнкцией двух высказываний x и y называется новое высказывание, истинное, когда оба истинны и ложно, когда одно из них ложно.

Обозначение: x^y или (x&y) «x и y».

X	y	x^y
0	0	0
0	1	0
1	0	0
1	1	1

x& x =0 – всегда ложно.

0 – всегда ложно.

3. Дизъюнкция (логическое сложение)

Дизъюнкцией 2-х высказываний x и y называется новое высказывание, истинное, если хотя бы одно из высказываний истинно и ложно, если оба ложны.

XvY или «x или y»

X	y	XvY
0	0	0
0	1	1
1	0	1
1	1	1

В треугольнике DEF углы D или E – острые.

XvX=1

4. Импликация

Импликацией двух высказываний x,y называется новое высказывание, которое ложно, если x-истинно, а y-ложно и истинно во всех остальных случаях.

X Y(«если X, то Y» или «из X следует Y».

X – условие или посылка,

Y – следствие или заключение.

Высказывание X Y – следование или импликация.

X	y	X Y
0	0	1
0	1	1
1	0	0
1	1	1

Пример. Если число 12 делится на 6, то оно делится на 3 – истинно.

Важно использование импликации при доказательстве теоремы.

5. Эквиваленция

Эквиваленцией двух высказываний X и Y называется новое высказывание, которое истинно, если оба высказывания одновременно истинны или одновременно ложны и ложно во всех остальных случаях.

X Y и читается «для того, чтобы X, необходимо достаточным, чтобы Y» или «X тогда и только тогда, когда Y».

X	y	X Y
0	0	1
0	1	0
1	0	0
1	1	1

Эквивалентность играет важную роль в математических доказательствах.

Формулы алгебры логики

(X^Y)vZ и X Yv(X^Y)

Пример формул алгебры логики.

Порядок действий:

Конъюнкция, дизъюнкция, импликация, эквивалентность.

Поэтому

(X^Y)vZ можно записать

X^Yv Z

X Yv(X^Y) можно записать

X YvX^Y

Пример таблицы истинности:

x v y x ^ y

X	y	x	y	XvY	X^Y	x v y x ^ y
0	0	1	1	1	0	0
0	1	1	0	1	0	0
1	0	0	1	0	1	1
1	1	0	0	1	0	0

Равносильность формул.

Две формулы А и В равносильны, если они принимают одинаковые логические значения на любом наборе входящих в формулу элементарных высказываний.

А=В – формулы А и В – равносильны

Х=Х;

XvX=X;

(X^X)vY=Y.

А – тождественно истине или тавтология, если она принимает значения 1 при всех значениях входящих переменных.

XvX=1; X (Y X)

Формула А – тождественно ложно, если она принимает 0 при всех значениях входящих переменных.

X^X=0

Отношение равносильности рефлексивно симметрично и транзитивно.

Если А и В равносильны, то А = В – тавтология и обратно, если А = В – тавтология, то А и В равносильны.

Важные равносильности алгебры логики можно разбить на 3 группы.

1. Основные равносильности.

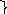1. X^X=X законы идемпотентности.

2. XvX=X

3. X^И=X

4. XvИ=И

5. X^Л=Л

6. XvЛ=X

7. X^X=Л – закон противоречия.

8. XvX=И – закон исключенного третьего.

9. X=X – закон снятия двойного отрицания.

10. X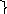^(YvX)=X законы поглощения.

Xv(Y^X)=X

Докажем 10.

А = X^(YvX)=X. Если Х=1, то YvX=1, тогда X^(YvX)=1.

Пусть Х=0; тогда X^(YvX)=0.

Итак, во всех случаях значения формулы А совпадает с Х, поэтому А=Х.

2. Равносильности, выражающие одни логические операции через другие.

1. X Y = (X Y)^(Y X)

2. X Y = XvY

3. X^Y=XvY

4. XvY=X^Y

5. X^Y=XvY

6. XvY=X^Y

Докажем 1.

Т.к. при одинаковых значениях X и Y истины X Y, X Y, Y X, то истины и конъюнкции (X Y)^(Y X). Следовательно, обе части равносильности имеют одинаковые истинные значения.

Пусть X и Y имеют различные логические значения. Тогда ложна X Y и одна из двух X Y или X Y, т.е., и конъюнкция (X Y)^(Y X).

Рассмотрим 3.

Если X и Y одновременно истинные, то истинно и X^Y и ложно

X^Y. В то же время ложны X, Y и XvY.

Пусть X илиY - ложь, тогда X^Y – ложь, X^Y – истина.

XvY – истина.

Аналогично доказывается 2 и 4.

Итак, всякую формулу можно записать как конъюнкцию, дизъюнкцию и отрицание – базовые операции!!!

Ясно, что 5 и 6 получить из 3 и 4, если от обеих частей отрицание и воспользоваться законом снятия двойного отрицания.

Однако, существует операция, с помощью которой можно выражать все 5 логических операций.

Штрих Шедуера.

X|Y

Таблица истинности:

X	y	X | Y
0	0	1
0	1	1
1	0	1
1	1	0

Очевидно:

1. X = X|X

2. X^Y = (X|Y)|(X|Y)

3. X|Y = X^Y.

Доказательство 3:

X	Y	X|Y	X^Y	X^Y
0	0	1	0	1
0	1	1	0	1
1	0	1	0	1
1	1	0	1	0

Доказательство 2:

X	Y	X^Y	X|Y	X|Y	(X|Y)|(X|Y)
0	0	0	1	1	0
0	1	0	1	1	0
1	0	0	1	1	0
1	1	1	0	0	1

Доказательство 1:

X	X	X|X
0	1	1
1	0	0

3.Равносильности, выражающие основные законы алгебры логики.

1. X^Y = Y^X – коммутативность конъюнкции

2. XvY = YvX – коммутативность дизъюнкции

3. X^(Y^Z) = (X^Y)vZ – ассоциативность конъюнкции

4. Xv(YvZ) = (XvY)vZ – ассоциативность дизъюнкции

5. X^(YvZ) = (X^Y)v(X^Z) – дистрибутивность конъюнкции относительно дизъюнкции.

Доказательство:

X	Y	Z	YvZ	X^(YvZ)	X^Y	X^ Z	(X^Y)v(X^Z)
0	0	0	0	0	0	0	0
0	0	1	1	0	0	0	0
0	1	0	1	0	0	0	0
0	1	1	1	0	0	0	0
1	0	0	0	0	0	0	0
1	0	1	1	1	0	1	1
1	1	0	1	1	1	0	1
1	1	1	1	1	1	1	1

6. Xv(Y^Z) = (XvY)^(XvZ) – дистрибутивность дизъюнкции относительно конъюнкции.

Доказательство:

X	Y	Z	Y^Z	Xv(Y^Z)	XvY	XvZ	(XvY)^(XvZ)
0	0	0	0	0	0	0	0
0	0	1	0	0	0	1	0
0	1	0	0	0	1	0	0
0	1	1	1	1	1	1	1
1	0	0	0	1	1	1	1
1	0	1	0	1	1	1	1
1	1	0	0	1	1	1	1
1	1	1	1	1	1	1	1

Можно 6 доказать так:

Если X = 1, то Xv(Y^Z) = 1;

XvY=1; XvZ=1; тогда и (XvY)^(XvZ)=1;

Итак, при Х=1 обе части равны 1;

Пусть Х=0, то Xv(Y^Z)=Y^Z; XvY=Y и XvZ=Z, а потому (XvY)^(XvZ)=Y^Z обе части равны Y^Z.

Примеры:

Доказать:

1) X Y=X^YvX^Y.

X Y = (X Y)^(Y X) = (XvY)^(YvX) = X^YvX^XvY^YvY^X = X^Yv0v0vY^X = X^YvY^X = X^YvX^Y.

2) (XvY X^Y)^Y

(XvYvXvY)^Y = (XvYvXvY)^Y= (XvY)^Y=Y;

3) (X Y) ((Y Z) (XvY Z)).

(X Y) ((Y Z) (XvY Z)) = (X Y)v(YvZvXvYvZ) = X^YvY^ZvX^YvZ = X^YvY^ZvX^YvZ = (X^YvX^Y)v(Y^ZvZ) = Y^(XvX)v(YvZ)^(ZvZ) = Y^1v(YvZ)^1 = YvYvZ = (YvY)vZ = 1vZ=1.

Итак, алгебра логики обладает коммутативным и ассоциативным законами относительно операций конъюнкции и дизъюнкции и дистрибутивным законом конъюнкции относительно дизъюнкции. В алгебре логики проводятся те же действия, что и в алгебре чисел.

Но в алгебре логики возможны и другие преобразования, основанные на использовании равносильностей:

(X^Y)vZ=(XvZ)^(YvZ);

X^(YvX)=X;

Xv(Y^X)=X;

X^Y=XvY;

XvY=X^Y и т.д.

Перейдем к обобщениям:

Рассмотрим непустое множество М элементов любой природы (X,Y,Z….), в котором определены отношения «=», и три операции «+», «*», «-» (сложение, умножение, отрицание), подчиняется следующим аксиомам:

Коммутативные законы:

1а) X+Y=Y+X;

1б) X*Y=Y*X;

Ассоциативные законы:

2а) X+(Y+Z)=(X+Y)+Z;

2б) X*(Y*Z)=(X*Y)*Z;

Дистрибутивные законы:

3а) (X+Y)*Z=(X*Z)+(Y*Z);

3б) (X*Y)+Z=(X+Z)*(Y+Z);

Законы идемпотентности:

4а) X+X=X;

4б) X*X=X;

Закон двойного отрицания:

5) X=X;

Законы Де – Моргана:

6а) X+Y=X*Y;

6б) X*Y=X+Y;

Законы поглощения:

7а) X+(Y*X)=X;

7б) X*(Y+X)=X.

Множество М – называется булевой алгеброй.

Если под X,Y,Z,…, понимать высказывание, под операциями +, *, - дизъюнкцию, конъюнкцию, отрицание, то все аксиомы алгебры булевой.

Если для некоторой системы аксиом удается подобрать конкретные объекты и конкретные соотношения между ними так, что все аксиомы выполняются, говорят, что найдена интерпретация (или модель) данной системы аксиом.

Итак, алгебра логики является интерпретацией булевой алгебры.

Алгебра Буля имеет и другие интерпретации. Например, если под основными элементами X,Y,Z множества М подразумевать множества, под операциями «+», «*», «-» - объединение, пересечение, дополнение соответствовали, а «=» - равенство множеств. В ней все аксиомы Буля выполняются.

Функции алгебры логики

Формула алгебры логики – функция входящих в нее элементарных высказываний. Например, формула (X^Y) Z является функцией трех переменных f(x,y,z). И аргументы, и функция принимают значения либо 0, либо 1.

Определение. Функция алгебры логики и переменных (функция Буля) – функции и переменных, где каждый принимает 2 значения 0 и 1 и функция 0 и 1.

Ясно, что тождественно истинные и тождественно ложные формулы алгебры логики – постоянные функции, а 2 равносильные функции – одна и та же функция. Сколько же имеется функций и переменных? Каждая функция задается таблицей истинности, содержащей 2 «строй. Функция «переменных принимает 2». Значит, состоящих из 0 и 1, т.е., набор значений из 0 и 1 длины 2».

Общее число наборов из 0 и 1, длин 2», равно 2 в степени 2ⁿ.

Различных функций 1 переменной – 4, 2^x – 16;

Рассмотрим таблицу истинности для различных функций 1 переменной. Она имеет вид:

X	F1(X)	F2(X)	F3(X)	F4(X)
1	1	1	0	0
0	1	0	1	0

Итак, 2 функции 1 переменной являются постоянными.

F₁(X)=1;

F₂(X)=Х;

F₃(X)=Х;

F₄(X)=0;

Таблица истинности функции 2 переменных:

X	Y	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15	F16
1	1	1	1	1	1	0	1	1	0	0	0	1	0	0	0	1	0
1	0	1	1	1	0	1	1	0	0	1	1	0	0	0	1	0	0
0	1	1	1	0	1	1	0	0	1	1	0	1	0	1	0	0	0
0	0	1	0	1	1	1	0	1	1	0	1	0	1	0	0	0	0

F₁=1

F₂=XvY

F₃=Y X

F₄=X Y

F₅=X^Y

F₆=X

F₇=X Y

F₈=X

F₉=X Y

F₁₀=Y

F₁₁=Y

F₁₂=XvY

F₁₃=Y X

F₁₄=X Y

F₁₅=X^Y

F₁₆=0.