
1-й сем-ДМ-слайды-ДГТУ / Графы-3,4 лекции / Маршр
..docxМаршруты, цепи и простые цепи1.
Пусть G- неориентированный граф.
Маршрут в
G– конечная или бесконечная
последовательность ребер
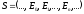 ,
,
В которой
два соседних ребра
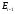 и
и
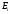 имеют общую концевую точку, т. е
имеют общую концевую точку, т. е
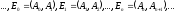 одно и то же ребро E может
встречаться в маршруте несколько раз.
одно и то же ребро E может
встречаться в маршруте несколько раз.
A1
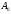 -
начальная вершина, нет ребер перед ней;
-
начальная вершина, нет ребер перед ней;
Ao
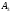 -
конечная вершина нет ребер после нее!
-
конечная вершина нет ребер после нее!
A2
A3
Любая
вершина, принадлежащая двум соседним
ребрам и
и
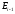 ,
называется внутренней или промежуточной
вершиной. Т. к ребра и вершины в маршруте
могут повторяться, внутренняя вершина
может оказаться начальной или конечной
вершиной. Маршрут называется нейтральным,
если он содержит хотя бы одно ребро;
маршрут, не содержащий никаких ребер,
называется нуль - маршрутом.
,
называется внутренней или промежуточной
вершиной. Т. к ребра и вершины в маршруте
могут повторяться, внутренняя вершина
может оказаться начальной или конечной
вершиной. Маршрут называется нейтральным,
если он содержит хотя бы одно ребро;
маршрут, не содержащий никаких ребер,
называется нуль - маршрутом.
Если маршрут
S имеет начальную вершину
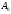 и конечную вершину
и конечную вершину
 ,
то
,
то
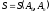 ,
,
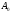 и
и
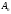 -
концы маршрута S. Говорят,
что S-маршрут длины n,
соединяющий
-
концы маршрута S. Говорят,
что S-маршрут длины n,
соединяющий
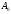 и
и
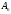 .
.
Если
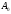 =
=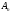 .
То маршрут называется циклическим.
.
То маршрут называется циклическим.
Для двух вершин маршрута Аi и Aj подмаршрут S(Ai , Aj)= (Ei , Ei+1 , Ej-1) называется
конечным участком S.
Маршрут называется цепью, а циклический маршрут - циклом, если каждое его ребро встречается в нем не более одного раза; вершины в цепи могут повторяться и несколько раз. Любой участок цепи есть цепь.
Нециклическая цепь называется простой цепью, если в ней никакая вершина не повторяется. Цикл с концом A0 называется простым циклом, если A0 не является в нем промежуточной вершиной и никакие другие вершины не повторяются. Участок простой цепи (цикла) -простейшая цепь (цикл)
Для ориентированного графа можно вводить как неориентированные маршруты, цепи и простые цепи, не принимая во внимание ориентации ребер, тем и ориентированные маршруты (цепи, простые цепи) в которых все ребра проходят в направлении их ориентации. Ориентированную цепь называют путем, ориентированный цикл – контуром.
Граф G называется связным, если для любых двух его вершин V и W существует простая цепь из V и W.
Любой граф можно разбить на непересекающиеся связанные подграфы, называемые компонентами (связности), задав отношение эквивалентности на множестве его вершин:
Две вершины эквивалентны (или связаны), если существует простая цепь из одной в другую. Связный граф состоит из одной компоненты. Граф несвязный, если число его компонент больше единицы
Если имея граф с n вершинами, заданным числом компонент. Если граф связан, то число ребер в нем минимально, когда он не имеет циклов (такой граф называется деревом) и максимальным, когда но – полный граф. Число ребер в таком графе m:
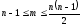 ;
;
Теорема
Пусть G
- простой граф с n
вершинами и k
компонентами. Тогда число его ребер:
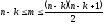
Следствие
Любой
простой граф с n
вершинами и более, чем
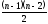 ребрами связан.
ребрами связан.
Насколько же сильно связан связный граф? Т. е сколько ребер нужно удалить из графа, чтобы он перестал быть связным?
Разделяющее множество связного графа G – множество его ребер, удаление которого приведет к несвязному графу.
Например, в графе, каждое из множеств
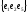 и
и
 является результирующим; несвязный
граф, оставшийся после удаления 2-го из
этих множеств, имеет вид:
является результирующим; несвязный
граф, оставшийся после удаления 2-го из
этих множеств, имеет вид:




e1 e5 e6 e4
e2 e7
e8



e1 e5 e4
e2
Назовем разрезом такое разделяющее множество, никакое собственное подмножество которого не является разделяющим.
Разрез
только множество
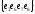 .
После удаления ребер , принадлежащих
разрезу, оставшийся граф, имеющий 2
компоненты ровно. Если разрез состоит
из 1 ребра e, то e
называется мостом или перешейком.
.
После удаления ребер , принадлежащих
разрезу, оставшийся граф, имеющий 2
компоненты ровно. Если разрез состоит
из 1 ребра e, то e
называется мостом или перешейком.
В произвольном графе G разделяющее множество – множество ребер, удаление которого увеличивает число компонент в G. Разрез в G – разделяющее множество, никакое собственное подмножество которого не является разделяющим.
мост



e


Теорема: Если в конечном графе G ровно две вершины a0 и b0 имеют четную локальную степень, то они связаны.
Доказательство: Каждый конечный граф имеет четное количество вершин нечетной степени. Так как это условие выполняется и для целой компоненты G, которой принадлежит a0, то b0 должно принадлежать той же компоненте. Кроме того, a0 и b0 должны остаться связанными в графе H, полученном из G удалением части H, в которой все локальные степени четные.
Теорема:
Если граф G с однократными
ребрами и без петель имеет n
вершин и k связанных
компонент, то максимальное число ребер
в G равно

Для случая K=2 имеем:
Граф с n
вершинами и с числом ребер, большем, чем
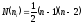 связен.
связен.
