1-й сем-ДМ-слайды-ДГТУ / Графы, л.5-7 / хроматические многочлены

Хроматические многочлены.

Пусть G – простой граф (без петель и циклов), пусть P_G (K) – число способов, которыми можно окрасить вершины графа G, используя К красок и соблюдая условие: никакие две смежные вершины не должны иметь один и тот же цвет.

Пусть P_G – хроматическая функция графа G.

Рассмотрим все возможные крайние случаи:

П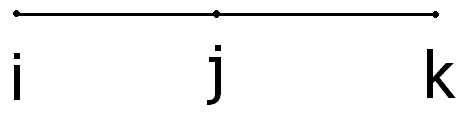усть имеем граф:

то P_G (K)=K(K-1)² , т.к. среднюю вершину можно окрасить К способами и каждую из концевых вершин (К-1)-способами. Всего К(К-1)² способов.

Обобщение.

Если T- произвольное дерево с n вершинами, то P_t(K)=K(K-1)^n-1.

Если G-полный граф K₃,то P_G(K)=K(K-1)(K-2); K₄, то P_G(K)=K(K-1)(K-2)(K-3) и т.д. Если К_n , то P_G(K)= K(K-1)(K-2). . . . . (K-n+1).

Ясно, что если K<X(G), то P_G(K)=0, если же K≥X(G):P_G(K)>0.

Теорема 7. Пусть G-простой граф, а V и W- его смежные вершины.

Пусть G₁ получен из G путем соединения ребром вершин V и W, а граф G₂-путем отождествления вершин V и W(и кратных ребер, если они при этом получаются). Тогда P_G(K)=P_G1(K)+ P_G2(K).(2)

Пусть имеем граф:

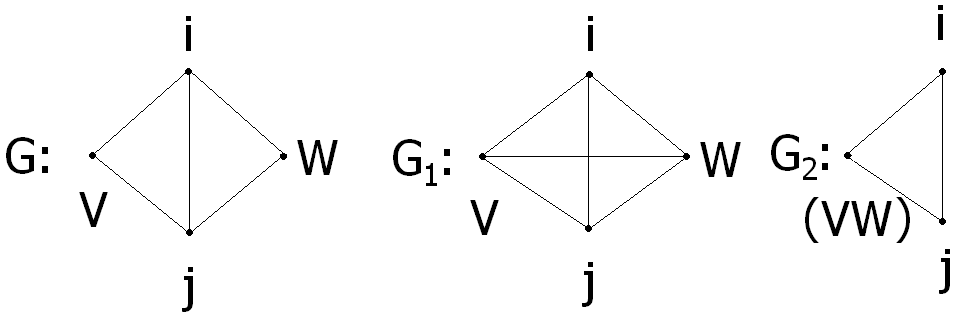
По теореме: К (К-1)(К-2)²=К (К-1)(К-2)(К-3)+К(К-1)(К-2)

(К (К-1)(К-2)[K-3+1])=K(K-1)(K-2)²;)

Доказательство. При любой допустимой раскраске вершин графа G либо V и W имеют разные цвета, либо они окрашены в один цвет. Число раскрасок, при которых V и W имеют разные цвета не изменится, если добавить ребро, соединяющее V и W,следовательно оно равно P_G1(K).Аналогично, число раскрасок, при которых V и W окрашены одним цветом , не изменится ,если отождествить V и W,следовательно оно равно P_G2(K).(G₁=G+l-граф полученный из G добавлением l; G₂=G l- замыкание вершин V и W).

Следствие. Хроматическая функция простого графа есть многочлен.

Доказательство.

Повторим процедуру, описанную в теореме 7,выбирая несмежные вершины в G₁ и G₂ соединяя и отождествляя их, в результате получим 4 новых графа. Снова повторяем. Процесс заканчивается, когда каждый граф- полный.

Следствие из теоремы 7.

Если l=(V,W)-ребро простого графа G, то P(G,K)=P(G-l,k)-P(G*l,k)(3),где G-l-получается из G удалением ребра l, a G*l- замыкание вершин V и W и замена параллельных ребер одним ребром.

Если повторно применить формулу (2) к графу G, то процесс закончится на графах: Н₁,Н₂,. . . ,Н_k,поэтому P(G,K)=P(H₁,k)+P(H₂,k)+. . .+P(H_k,k);

Если использовать формулу (3), то процесс закончится на пустых графах без ребер => хроматический полином – множество комбинаций полиномов пустых графов.

Теорема Карона.

Граф G – двух раскрашиваемый тогда и только тогда, когда G- Эйлеров граф.

1)нижние оценки:

γ(G)≥ρ(G),

γ(G)≥ , где n-число вершин

m- число ребер.

2)верхние оценки:

γ(G)≤1+max[P(x_i)+1]

x_i Є x

Алгоритм раскраски.

Пусть множество вершин угла вершины этого множества.

1)Окрасить х_i в цвет 1.

2)Каждую из оставшихся вершин окрасить: X_i- в цвет с наименьшим возможным номером (не использованным при окраске вершины смежной с X_i ).

Связь с задачей расписание.

Пусть нужно выбрать время проведения лекций по разным предметам с учетом того, что студенты желают посещать и те, и другие.

Строим граф. Вершина его - лекции по разным предметам, а ребра соединяют те пары лекций, которое не должны назначаться на одно и то же время.