1-й сем-ДМ-слайды-ДГТУ / Графы, л.5-7 / Вершинная К раскраска графа
.docРаскраска графа. Хроматические полиномы. Алгоритм раскраски.
Вершинная К раскраска графа-присвоения его вершинам К различных цветов. Никакие 2 не должны быть одного цвета.
--
правильная 3-раскраска
Хроматическое число Х(G) –минимальное число К, для которого G вершина К –раскрашиваемый Х(G)=К –граф –хроматический.
К - раскраска графа G=(V,E)
порождает разбиения (V1,
V2, V3,
)
множества V, где каждое
-подмножество
вершин, которым присвоен цвет i
–независимо множества.
Теорема
Простой граф G –(
)
раскрашиваемый (
- максимальная степень в графе G)
Очевидно, что Х = (
)
для полных графов и циклов нечётные
длины. Для остальных графов Х
Хроматические полиномы
Две раскраски графа считаются различными, если хотя бы одной вершине присваиваются разные цвета.
Хроматические полиномы Р(G,
)
имеют значения для каждого целого
,
равное числу различных правильных
раскрасок графа G. (
)
Раскрасим любым цветом из
в один из оставшихся
-1
цветов. Для каждой раскраски существует
-1
различных способов раскраски вершин
С.
Итак, граф (
)
можно раскрасить
различными способами, то хроматический
полином графа равен
Хроматический полином пути на n
вершинах равен
Пример. Рассмотрим граф
c
вершинами V1,V2,V3……
.При
наличии
цветов V1- в любой из них
, V2-
-1,
V3 -
-2
и т.д.
Путь U и V – несмежные вершины G.
Пусть е(U,V)
; Если G*
е- простой граф, получен из G
замыканием вершин U и V
и заменой получившегося множества
параллельных рёбер на 1 ребро, а G+е
– граф полученный добавлением к
G ребра
е то Р(G,
)=
Р(G+е,
)+Р(G*
е,
)
Следствие
Если е(U,V)-
ребро простого графа G,
то Р(G,
)=
Р(G+е,
)-
Р(G*
е,
)
, где G-е
– получается из G
удаления ребра е
, а G*
е – замыканием вершин U
и V
Если мы имеем полные графы : H1,
Н2, Н3….
поэтому Р(G,
)=Р(Н1,
)+Р(Н2,
)+….Р(
,
)
Итак, хроматический полином – линейная комбинация хроматических полиномов пустых графов.
Теорема
Хроматический полином. Р(G,
)
графа G на вершинах имеет
степень n с главным членом
и const.=0 Все коэффициенты
целые и чередуются …….
Пусть граф G с n вершинами и m рёбрами. е – ребро G .Тогда G- е -граф на n вершинах с m-1 рёбрами , а G* е - граф на n-1 вершинах с m-1 или менее рёбрами.
Оценки:
Нижние:
Верхние оценки:
Алгоритм раскраски
Пусть множество вершин упорядочено и
-я
вершина этого множества
-
окрасить
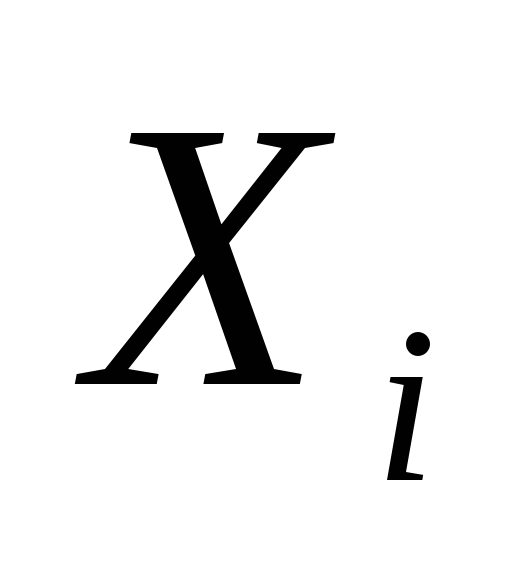в цвет 1 -
Каждую из оставшихся вершин окрасить :
в цвет с наименьшим возможным номером
( не используя при окраске вершин смежной
с
.
Если граф G –К –раскрашиваемый
, но не является (К-1)раскрашиваемым , а
число К- хроматическое число графа G,
обозначим Х(G)
4-хроматический граф, цвета (
)
Теорема
Если наибольшая из степеней вершин
графа G равна Р , то этот
граф
-раскрашиваемый.
Теорема Брукса
Пусть наибольшая из степеней вершин графа равна Р. Тогда G-P- раскрашиваемый, за исключением тех случаев ,когда
-
G содержит в качестве компонента граф
или
-
Р=2 и цикл нечётной длинны является компонентой G
-
полный граф степени Р+1
Теорема
Любой планарный граф G – раскрашиваемый.
Теорема
Каждый планарный граф 5 раскрашиваемый.
Гипотеза 4-х красок
Всякий планарный граф 4-раскрашиваемый.
-
Всякий планарный граф, имеющий менее 52 вершин -4раскрашиваемый
-
Любой, не содержащий треугольников планарный граф 3-раскрашиваемый
-
Гипотеза 4-х красок верна для гамильтоновых планарных графов.
Карта- связный плоский граф без мостов.
- 3-раскрашиваемый и вершинно 4-х раскрашиваемый
Всякая карта -4-х раскрашиваемая
Теорема
Карта G -2-х – раскрашиваемая тогда и только тогда , когда G – эйлеров граф.
Теорема Визинга
Пусть G –простой граф, а
V и W – его
несмежные вершины. Пусть граф
получается из G путём
соединения ребром вершин V
и W, а граф
-путём
отождествления вершин V
и W( и кратных рёбер , если
они при этом получаются)Тогда
Дан граф
Многочлен имеет вид:
(а,
в, с –положительный const.)
Пример.
=
+
Итак,
=
+
=
+
+
+
=
+
+2
+
Итак,
(К)=К
(К-1)(К-2)(К-3)(К-4)+3К (К-1)(К-2)(К-3)+2К (К-1)(К-2)=К
(К-1)(К-2)
=
Хроматический полином Р (G,
)
имеет значение для каждого целого
, равное числу различных правильных
-раскрасок
графа G. Рассмотрим граф
Среди данных
цветов мы можем выбрать любой для
раскраски вершин а. Вершину b
можно раскрасить в один из оставшихся
-1 цветов. Для каждой раскраски вершины
b существует
-1
различных способов раскраски вершины
С. Итак, данный граф можно раскрасить
различными способами. Хроматический
полином графа равен
.Повторяя
эти рассуждения , получим, что хроматический
полином пути на n вершинах
равен
Другим важным крайним случаем является
полный граф
,
имеющий n вершин. При ….
цветов вершину
можно раскрасить в любой из них,
-в
любой из оставшихся
-1
цветов, вершину
-в
любой из оставшихся
-2
цветов. Итак, Р (
)=
(
-1),
и (
-n+1)
Выведем формулу для определения хроматического полинома графа G.
Теорема 7
Пусть U и V – несмежные вершины простого (без петель и циклов) графа G. Пусть е=(U,V)
Если G*e
– простой граф полученный из графа G
замыканием вершин U и V
и заменой получившегося множества
параллельным ребёр на одно ребро, а G+e
– граф, полученный добавлением к графу
G ребра е
, то Р(G
,)=Р(G+е,
)+Р(G*e,
).
Док-во:
Любая
- раскраска графа G , в
которой вершинам U и V
присваиваются различные цвета ,
соответствует
-раскраска
графа G+e
, и наоборот .Аналогично, любая
-раскраска
графа G , в которой U
и V присвоен 1 цвет,
соответствует
-раскраска
графа G*e
, и наоборот .
Следовательно, Р(G,
)=Р(G+е,
)+Р(G*e,
).
Можно сформулировать следствие
Если е=(U,V)
–ребро простого графа G,
то Р (G,
)=Р(G-е,
)+Р(G*e,
),
где G-е
получается из G
удалением ребра е,
а G*e
определяется в теореме.
Если повторно применить формулу,
приведённую в теореме 7 к графу G,
то процесс закончится полных графах,
например,
поэтому
Р(G,
)=
С другой стороны, если использовать формулу следствия , то процесс закончится на пустых графах (без ребер), поэтому хроматический полином- линейная комбинация хроматических полиномов пустых графов.
Хроматический полином пустого графа
на n вершинах
Следствие. Хроматические функции простого графа представляет собой многочлен.
Док - во: Повторим процедуру, описанную в теореме 7, выбирая несмежные вершины в G1 и в G2 и соединяя и отождествляя их, в результате получим 4 новых графа. Процесс заканчивается, когда каждый граф – полный. Итак, хроматическая функция графа G является суммой многочленов и поэтому сама должна быть многочленом.
-
хроматический многочлен графа G.
Если G имеет n
вершин, то степень
равен
n , т.к. на каждом шаге не
возникает новых вершин, т.к. G
–полный граф с n вершинами
, то коэффициент при
=1
Коэффициент при
равен m , где m
число рёбер в G. Знаки
коэффициентов чередуются .Постоянный
член хроматического многочлена равен
0 , т.к. если нет красок , то нельзя
раскрасить граф.
Пример 1
=
+
=
+
+
Р
=
(
-1)(
-2)(
-3)+2
(
-1)(
-2)
+
(
-1)
+
(
-1)=
(
-1)
=
(
-1)
=
+
=
+
+
+
=
+
+2
+
+
P(G)=К(К-1)(К-2)(К-3)(К-4)+3К(К-1)(К-2)(К-3)+2К(К-1)(К-2)=
=
G- 3-хроматический граф.
Связь с задачей раскраски
Пусть нужно выбрать время проведения лекций по различным предметам с учетом того , что студенты желают посещать и те и другие. Строим граф. Вершины его- лекции по различным предметам , а рёбра соединяют те пары лекций, которые не должны назначаться на 1 время. Если каждому предмету для лекции времени сопоставить некоторый цвет, то раскраски- правильное расписание. Хроматический многочлен покажет, можно ли составить расписание требуемым образом , если да, то сколькими способами.
Пример
=
+
=
+2
+
=
+3
+
На
некотором шаге выбираем 2 вершины U,Vn: