
дгту / каспарян / математика / Математика к.р.1
.docx
Контрольная работа №1
Вариант 9.
Задание 1. Дана матрица
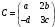 .
Найти матрицу R = C2
– 2CT
-3C-1.
.
Найти матрицу R = C2
– 2CT
-3C-1.
а = -2, b = -2, c = 3, d = 1.
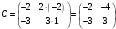 ,
,
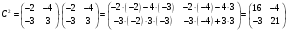 ,
,
 ,
,
Найдем обратную матрицу С-1.
Главный определитель:
∆=(-2•3-(-3•(-4)))=-18
Алгебраические дополнения транспорированной матрицы:
С11=(-1)1+1·3=3; С12=(-1)1+2·-4=4; С21=(-1)2+1·-3=3; С22=(-1)2+2·-2=-2;
Тогда обратная матрица имеет вид:
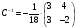
Проверим правильность нахождения обратной матрицы, умножив исходную матрицу на обратную. Должны получить единичную матрицу E.
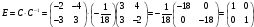
Найдем матрицу R:
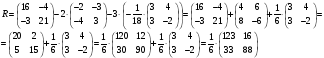
Задание 2. Дана система уравнений АХ = В, где матрицы
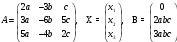
а = -2, b = -2, c = 3, d = 1.
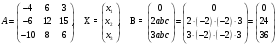
Решить систему уравнений тремя методами:
а) по формулам Крамера,
б) матричным методом,
в) Методом Жордана-Гаусса.
а) Решение СЛАУ методом Крамера:
Найдем главный определитель матрицы:
 Δ
= -4.(12.6-8.15)
– 6(-6.6
– (-10)
.15)
+ 3(-6.8
– (-10)
.12)
= 192 -684 + 216 = -276.
Δ
= -4.(12.6-8.15)
– 6(-6.6
– (-10)
.15)
+ 3(-6.8
– (-10)
.12)
= 192 -684 + 216 = -276.
Заменим 1-ый столбец матрицы А на вектор результата В:

Δх1 = – 6(24.6 – 36 .15) + 3(24.8 – 36 .12) = 2376 - 720 = 1656.
Заменим 2-ый столбец матрицы А на вектор результата В

Δх2 = -4.(24.6-36.15) + 3(-6.36 – (-10) .24) = 1584 + 72 = 1656.
Заменим 3-ый столбец матрицы А на вектор результата В

Δх3 = -4.(12.36-8.24) - 6(-6.36 – (-10) .24) = -960 - 144 = -1104.
Неизвестные переменные xi:
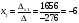
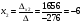
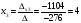
Проверка: -4.-6+6.-6+3.4 = 0.
-6.-6+12.-6+15.4 = 24.
-10•-6+8•-6+6•4 = 36.
б) Решение матричным методом:
Найдем главный определитель матрицы:
 Δ
= -276 – система будет иметь решение, так
как определитель не равен нулю.
Δ
= -276 – система будет иметь решение, так
как определитель не равен нулю.
Найдем обратную матрицу через алгебраические дополнения транспорированной матрицы:

Алгебраические дополнения.
A11 = (-1)1+1(12.6 – 15.8) = 72 – 40 = 32,
A12 = (-1)1+2(6.6 – 3.8) = -(36 – 24) = -12,
A13 = (-1)1+3(15.6 – 3.12) = 90 – 36 = 54,
A21 = (-1)2+1(15.(-10) – 6.(-6)) = -(-150 + 36) = 114,
A22 = (-1)2+2(-4.6 – 3.(-10)) = -24 + 30 = 6,
A23 = (-1)2+3(-4.15 – 3.(-6)) = -(-60 + 18) = 42,
A31 = (-1)3+1(-6.8 – 12.(-10)) = -48 + 120 = 72,
A32 = (-1)3+2(-4.8 – 6.(-10)) = -(-32 + 60) = -28,
A33 = (-1)3+3(12.(-4) – 6.(-6)) = -48 + 36 = -12,
Обратная матрица:
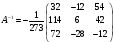
Вектор результатов:
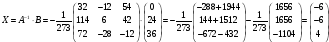
Проверка: -4.-6+6.-6+3.4 = 0.
-6.-6+12.-6+15.4 = 24.
-10•-6+8•-6+6•4 = 36.
в) Решение методом Гаусса:
Составим расширенную матрицу:

Проведём следующие действия:
К строке 2 добавим: −1,5 × Строку 1.
К строке 3 добавим: −2,5 × Строку 1.
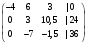
Разделим строку 1 на разрешающий элемент, равный (-4).
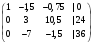
К строке 1 добавим: 0,5 × Строку 2.
К строке 3 добавим: 7/3 × Строку 1.

Разделим строку 2 на разрешающий элемент, равный 3.

Разделим строку 3 на разрешающий элемент, равный 23.

К строке 1 добавим: -4,5 × Строку 3.
К строке 3 добавим: -3,5 × Строку 3.

Проверка: -4.-6+6.-6+3.4 = 0.
-6.-6+12.-6+15.4 = 24.
-10•-6+8•-6+6•4 = 36.
Задание
3.
Векторы
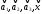 заданы
своими координатами в каноническом
базисе
заданы
своими координатами в каноническом
базисе
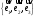 .
Требуется:
.
Требуется:
а)
показать, что система векторов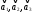 образует базис в пространстве R3.
образует базис в пространстве R3.
б)
записать матрицу перехода от канонического
базиса
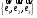 к базису
к базису
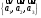 и
разложить вектор
и
разложить вектор
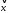 по этому базису.
по этому базису.
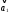 =
(4,2,3)
=
(4,2,3)
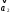 =
(1, -3, 1)
=
(1, -3, 1)
 =
(-2, 0, -2)
=
(-2, 0, -2)
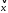 =
(3, 2, -1)
=
(3, 2, -1)
а)
Система векторов линейного пространства
образует базис в R3,
если эта система векторов упорядочена,
линейно независима и любой вектор
линейно выражается через векторы
системы. Составим матрицу из векторов
 :
:

Вычислим определитель основной матрицы:
Δ = -2.(2.1-3.(-3)) - 2(-3.4 – 1 .2) = -22 + 28 = 6.
Так как определитель матрицы
не равен нулю (6 0),
то векторы
0),
то векторы
 линейно
независимы и образуют базис в трехмерном
пространстве R3.
линейно
независимы и образуют базис в трехмерном
пространстве R3.
б)
Запишем матрицу перехода от канонического
базиса
 к
к
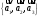 .
.
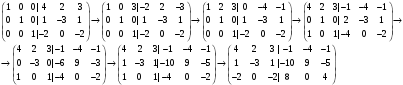
Провели следующие преобразования:
1) 3 строку умножили на 3 и прибавили к 1;
2) 2 строку умножили на 2 и прибавили к 1;
3) 3 столбец прибавили к первому столбцу;
4) 2 строку умножили на (-3);
5) 3 строку прибавили ко 2 строке;
6) 3 строку умножили на (-2).
Матрица перехода имеет вид:
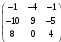
Разложим вектор
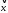 по полученному базису. Для разложения
вектора по базису запишем векторное
уравнение: с1a1
+ с2a2
+ с3a3
= х. Перепишем векторное уравнение в
матричном виде и решим его методом
Гаусса.
по полученному базису. Для разложения
вектора по базису запишем векторное
уравнение: с1a1
+ с2a2
+ с3a3
= х. Перепишем векторное уравнение в
матричном виде и решим его методом
Гаусса.
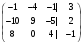

Задание 4.
Элементы матрицы С4х5 заданы по вариантам заданы по вариантам:

1. Считая матрицу С4х5 матрицей однородной СХ = 0, найти для этой системы
а) фундаментальную систему решений;
б) общее решение;
в) какое-нибудь частное решение.

Применяя к расширенной матрице, последовательность элементарных операций стремимся, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.
|
Разделим строку 1 на a1,1 = |
2 |
Получим матрицу :
|
|
Вычтем из строки 2 строку 1 умноженную на a2,1= |
5 |
Вычитаемая строка :
|
|
|
|
Модифицированная матрица :
|
|
Вычтем из строки 3 строку 1 умноженную на a3,1= |
6 |
Вычитаемая строка :
|
|
|
|
Модифицированная матрица :
|
|
Вычтем из строки 4 строку 1 умноженную на a4,1= |
3 |
Вычитаемая строка :
|
|
|
|
Модифицированная матрица :
|
|
Разделим строку 2 на a2,2 = |
|
Получим матрицу :
|
