0

Одесский Национальный Университет

им. И.И.Мечникова

НЕБЕСНАЯ МЕХАНИКА

ОПРЕДЕЛЕНИЕ ЭЛЕМЕНТОВ ОРБИТ

Метод Гаусса

Метод Ольберса

Кафедра астрономии

Базей Александр Анатольевич

Одесса 2002

ЛИТЕРАТУРА

1. Субботин М.Ф. «Введение в теоретическую астрономию», Наука, Москва 1968, 800с.

2. Дубяго А.Д. «Определение орбит», Москва, Ленинград 1949, 444с.

ОПРЕДЕЛЕНИЕ ЭЛЕМЕНТОВ ЭЛЛИПТИЧЕСКОЙ ОРБИТЫ ПО ТРЕМ НАБЛЮДЕНИЯМ МЕТОДОМ ГАУССА

ПОСТАНОВКА ЗАДАЧИ

Для определения элементов орбиты необходимо знать координаты и составляющие вектора скорости одного тела относительно другого. Наблюдение с движущейся Земли дает лишь направление прямой, соединяющей наблюдателя с светилом, и ничего не говорит о расстоянии до него. Отсюда возникает необходимость получения добавочных наблюдений.

Движение светила вокруг Солнца без учета притяжения других тел определяется посредством 6-ти постоянных величин, входящих в решение дифференциальных уравнений движения задачи 2-х тел. Обычно используют кеплеровы элементы орбиты.

Такое решение удовлетворительно представляет действительное движение светила на протяжении небольшого промежутка времени пока можно пренебречь влиянием других небесных тел. Поэтому способы определения орбит строятся в предположении, что имеющиеся наблюдения немногочисленны и близки по времени. {1}

Поскольку наблюдения производятся с Земли, то очевидно

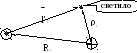
Каждое наблюдение объекта дает для определенного момента t_i прямое восхождение и склонение и позволяет написать три уравнения связи:

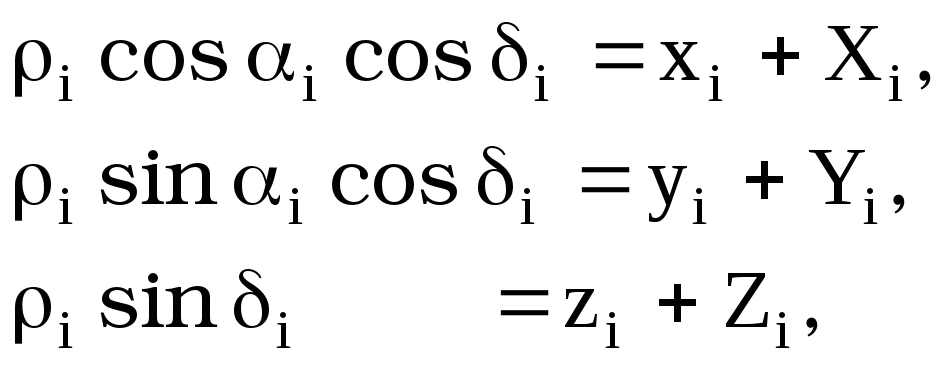[1]

где - геоцентрические прямоугольные экваториальные координаты Солнца;

- геоцентрические расстояния светила;

- гелиоцентрические прямоугольные экваториальные координаты светила.

Так как геоцентрические координаты Солнца известны, то неизвестными величинами в этих уравнениях являются геоцентрические расстояния и гелиоцентрические координаты светила. Причем эти гелиоцентрические координаты выражаются через 6 элементов орбиты. Таким образом, для одного наблюдения будем иметь 3 уравнения и 6+1 неизвестное, для двух наблюдений – 6 уравнений и 6+2 неизвестных. В случае трех наблюдений i = 1,2,3 система [1] состоит из 9-ти уравнений с 9-ю неизвестными –

.

Таким образом, для нахождения элементов орбиты необходимо иметь по крайней мере 3 наблюдения. {2}

Процесс определения орбит можно разделить на два основных этапа: первичное определение орбиты и улучшение орбиты. Первичное определение орбиты – это приближенное построение первоначально полностью неизвестной орбиты из некоторого числа наблюдений. При улучшении орбиты уточняют уже приблизительно известные элементы.

ВОПРОСЫ.

1. Почему для определения элементов орбиты светила требуются немногочисленные и близкие во времени наблюдения?

2. Чему равно минимальное количество наблюдений, необходимое для определения элементов орбиты и почему?

Идея метода гаусса

Метод Гаусса основан на интегралах уравнений движения. Этот метод требует знания сферических координат для трех моментов времени и соответствующих положений Земли относительно Солнца. Три наблюдения представляют тогда три точки орбиты наблюдаемого небесного тела. Эти точки удовлетворяют трем следующим условиям:

• они лежат в той же плоскости, что и центр Солнца;

• они лежат на коническом сечении (в рамках задачи 2-х тел);

• площади секторов, ограниченных радиусами-векторами орбиты небесного тела удовлетворяют II закону Кеплера.

Итак, имеется три точки - положения Земли, из этих точек проводится три направления на светило – рисунок слева.

Затем направления 1, 2, 3 надо пересечь плоскостью, проходящей через центр Солнца, причем так, что если провести через точки пересечения 1, 2, 3 коническое сечение, то согласно II закону Кеплера удвоенные площади секторов между и , соответственно и равны:

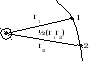[2]

Из этих соображений можно найти положение плоскости орбиты, которое вполне характеризуется двумя параметрами, например .

Если удалось найти положение плоскости орбиты светила, тогда можно определить и точки пересечения наблюденных направлений на светило с плоскостью его орбиты. То есть в системе [1] будут найдены геоцентрические расстояния светила . Итак, истинные должны одновременно удовлетворять системам [1] и [2].

В способе Гаусса такие отыскиваются методом последовательных приближений.

В системе [2] параметр орбиты p и удвоенные площади секторов и неизвестны. Обозначим удвоенные площади треугольников между радиус-векторами и хордами орбиты и .

Полагая известными из системы [1] можно получить гелиоцентрические координаты светила , а значит и площади , .

Введем обозначение - отношение площади сектора к площади соответствующего треугольника.

Гаусс показал, что по заданным положениям светила и промежуткам времени можно отыскать с любой точностью, без знания элементов орбиты. {2}

Таким образом, задавшись приближенными , находим удвоенные площади треугольников , по способу Гаусса вычисляем и находим удвоенные площади секторов , из формул [2] уточняем значение параметра и, следовательно .

Далее снова из находим координаты светила , удвоенные площади , и вычисляем новые .

Повторяя этот процесс надо добиться совпадения последовательных значений . Это покажет, что полученные удовлетворяют условиям задачи.

Наконец, зная гелиоцентрические координаты светила и отношения площадей секторов к площадям треугольников можно получить элементы орбиты, пользуясь лишь геометрическими свойствами конических сечений.

ВОПРОСЫ.

1. В чем заключается идея метода Гаусса определения элементов эллиптической орбиты?

2. Какую величину 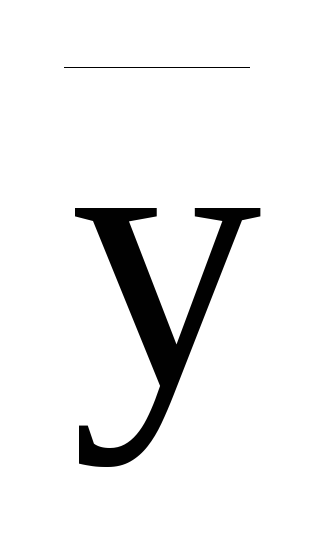ввел Гаусс, и с какой целью?

Уравнение плоскости орбиты светила

Пусть

[3]

есть уравнение плоскости, проходящей через центр Солнца, причем хотя бы один из коэффициентов A, B, C не равен нулю. Допустим, что [3] есть уравнение плоскости орбиты светила. Тогда координаты светила должны удовлетворять [3]:

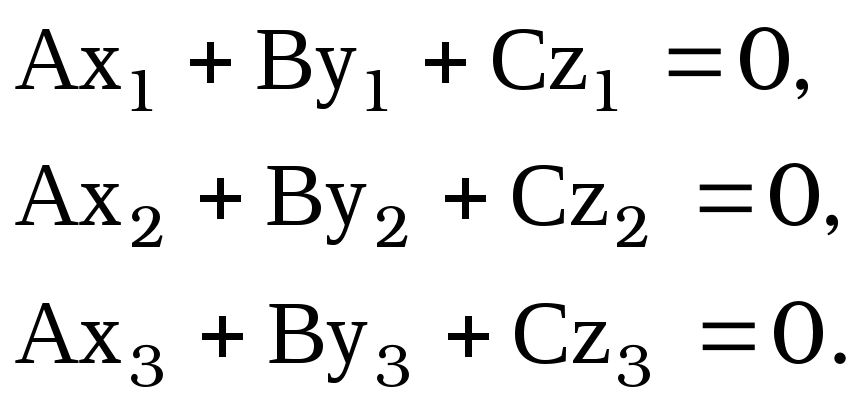[4]

Чтобы плоскость орбиты существовала, [4] должна иметь нетривиальное решение относительно A, B, C (хотя бы один из A, B, C был не равен нулю!). Для этого должно выполняться условие

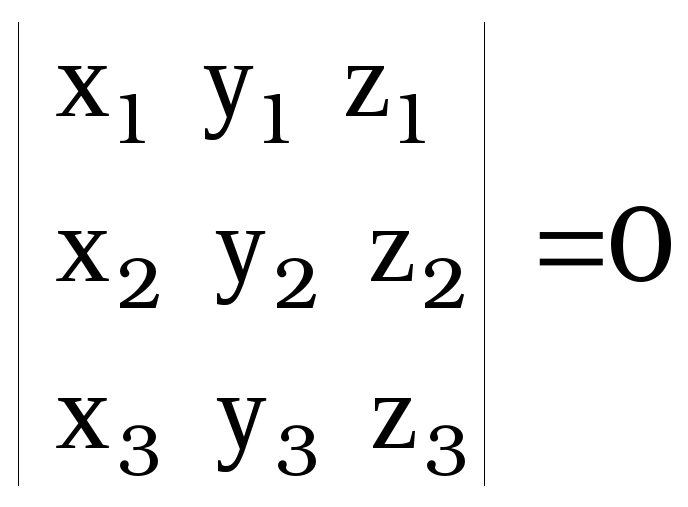[5]

Разлагая определитель по элементам столбцов:

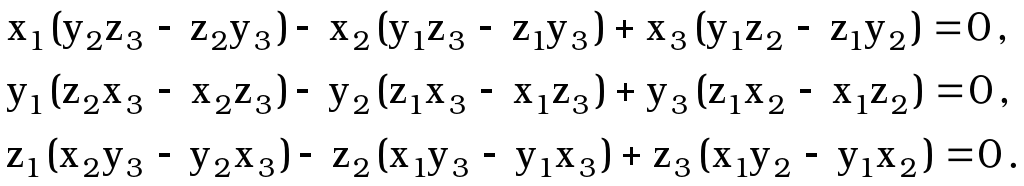[6]

Эти уравнения отличаются лишь циклической перестановкой букв. Заметим, что выражения, стоящие в скобках, не что иное, как удвоенные площади проекций треугольников на три координатные плоскости, которые могут быть определены через векторные произведения соответствующих радиусов - векторов, например,

.

Здесь - угол между нормалью к плоскости орбиты и осью OX. Направляющие косинусы нормали можно вынести за скобки и учитывая структуру уравнения, получаем [6] в виде:

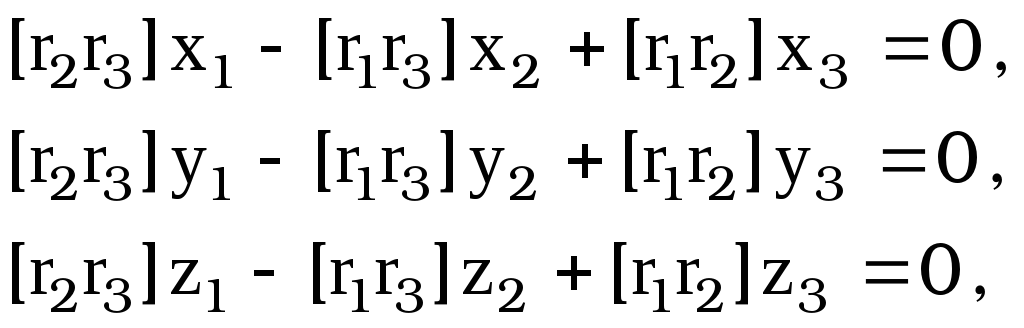[7]

где введено обозначение .

Сокращение на направляющие косинусы эквивалентно тому, что если в каждом уравнении три площади проектируются на одну плоскость, то вместо их проекций могут быть взяты сами треугольники.

Разделим систему [7] на и положим

[8]

это даст

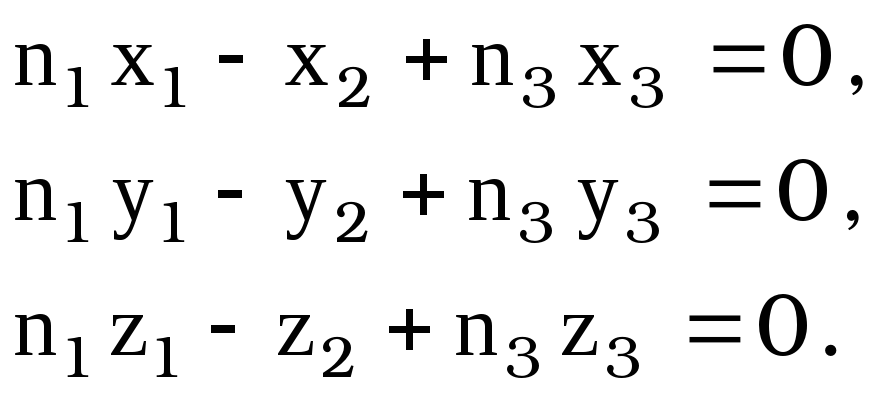[9]

В уравнениях [1] направляющие косинусы луча зрения (левые части уравнений) обозначим

[10]

тогда система [1] запишется:

[11]

Подставляя [11] в [9], получим

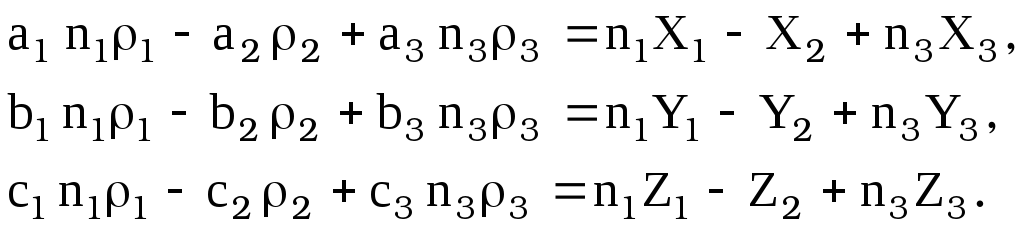[12]

Здесь содержится пять неизвестных - . Эту систему можно разрешить относительно , но тогда надо считать известными. Если взять для приближенные значения, то мы найдем приближенные , и при дальнейшем уточнении будут уточняться и .

Определим , для этого исключим из системы [12] . Используем правило Крамера: неизвестное равно отношению определителя, составленного из коэффициентов, в котором столбец коэффициентов при неизвестном заменен столбцом свободных членов и определителя, составленного только из коэффициентов:

[13]

где ,

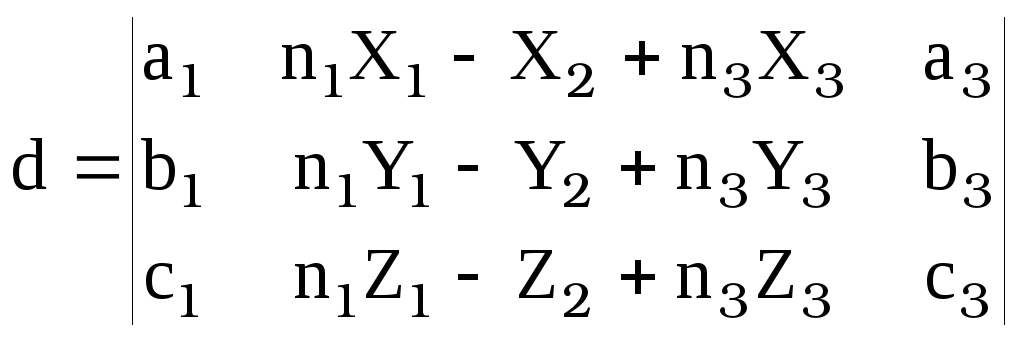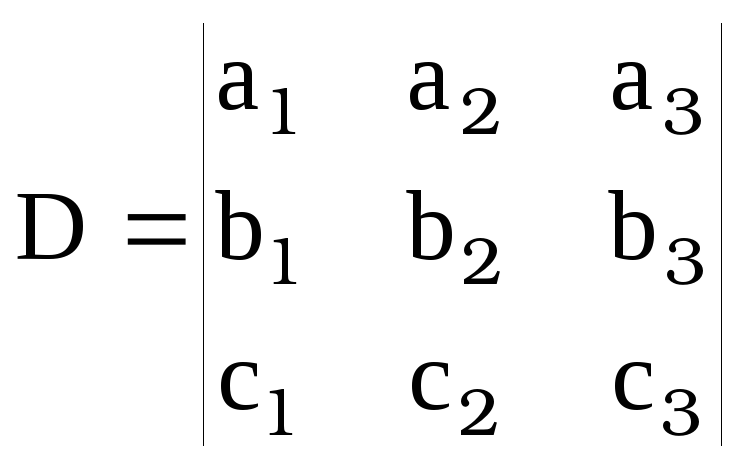
“-“ во втором столбце определителя D вынесен за знак определителя в [13]

или

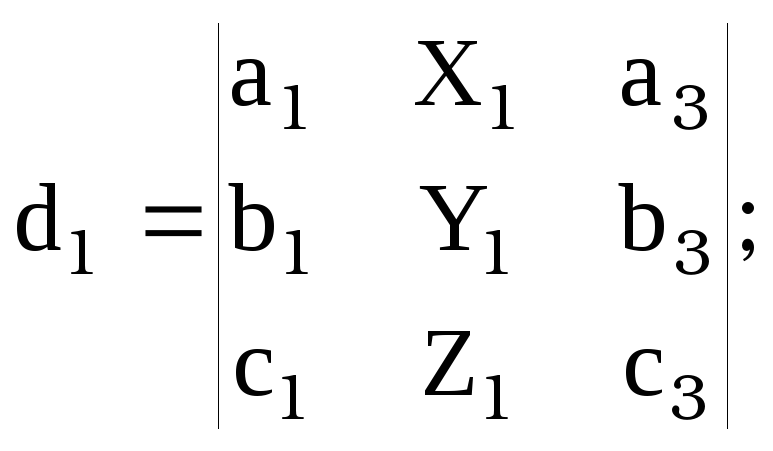
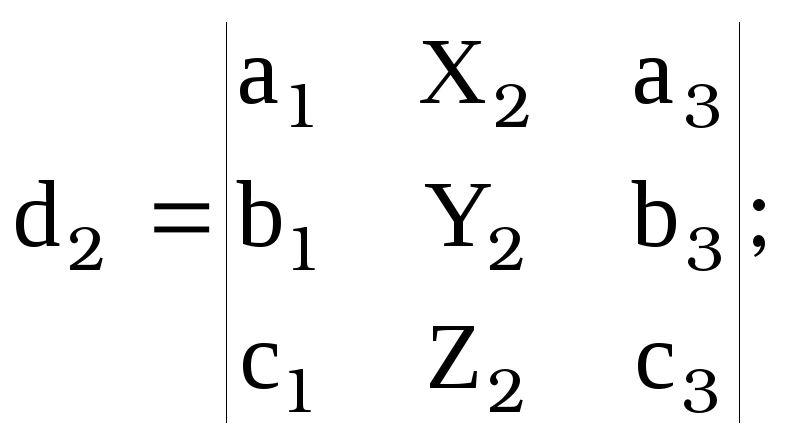
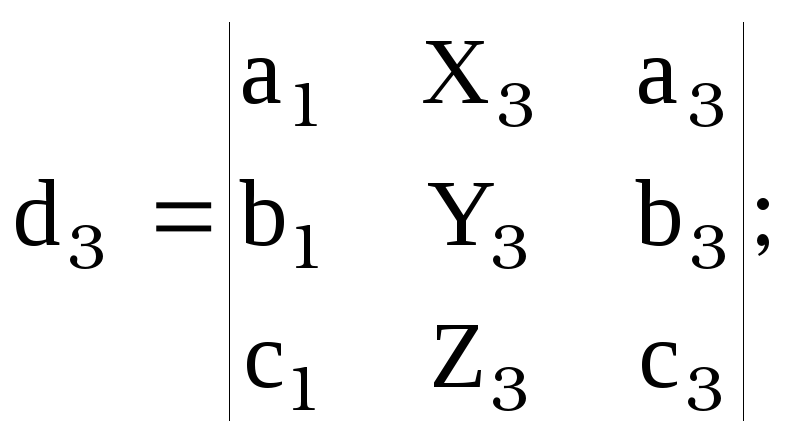
, где

, где , , 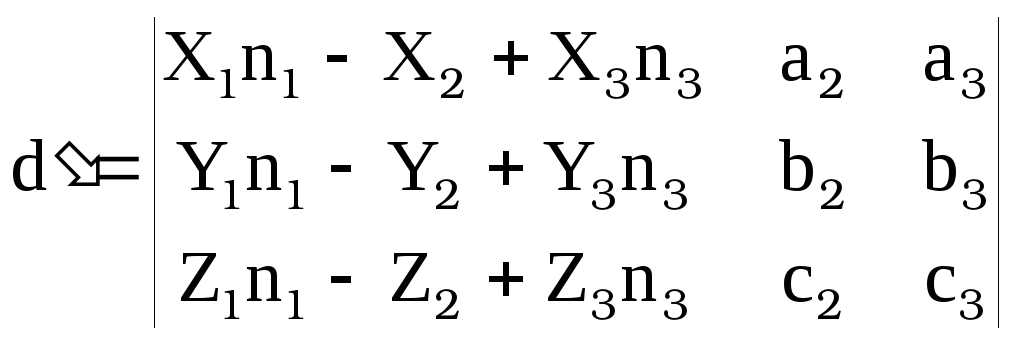[14]

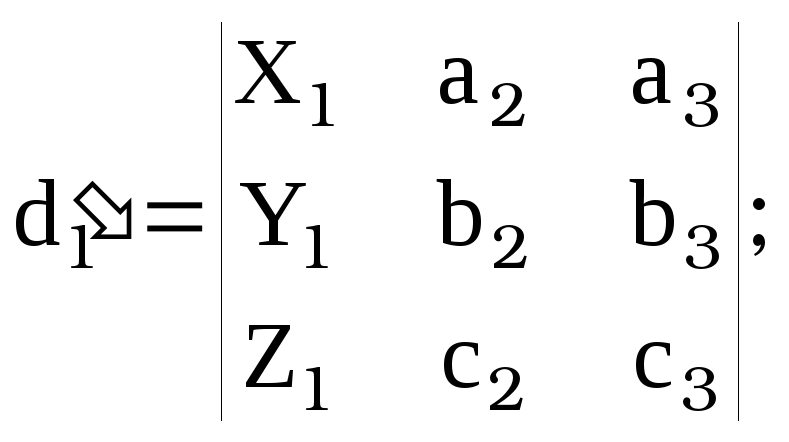
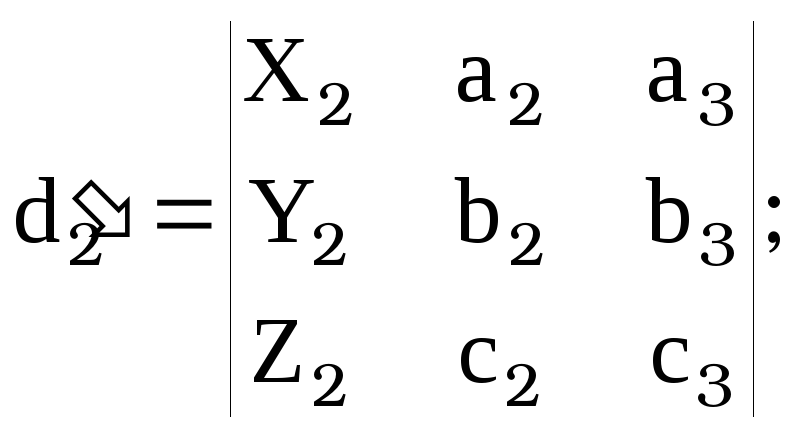
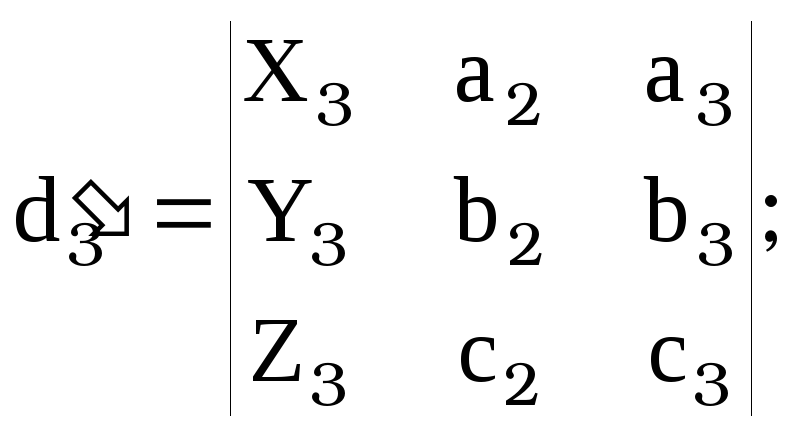
, где , ,

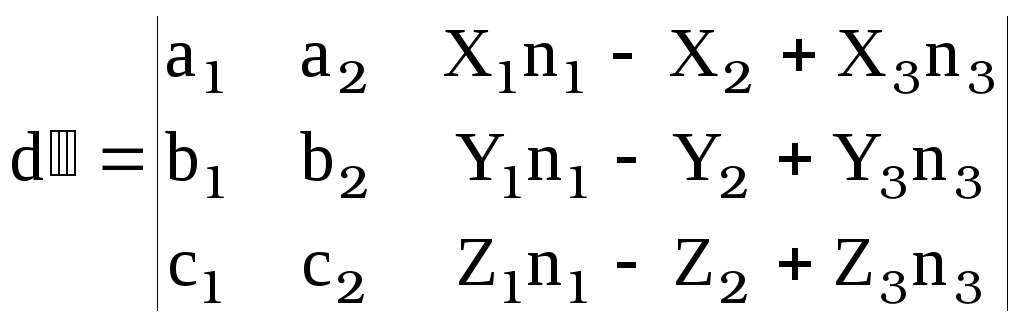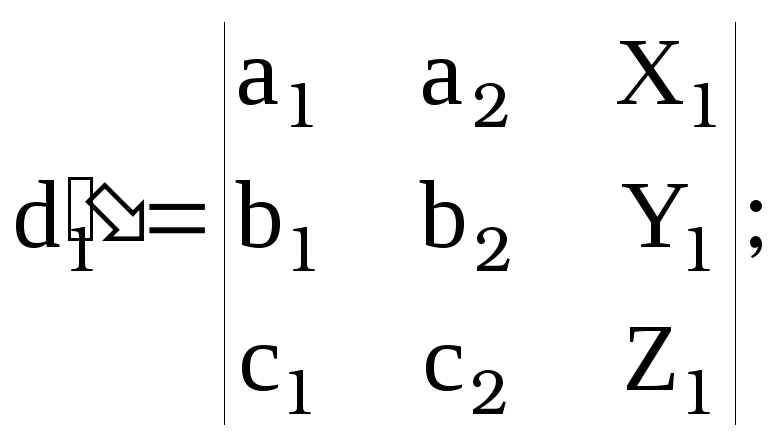
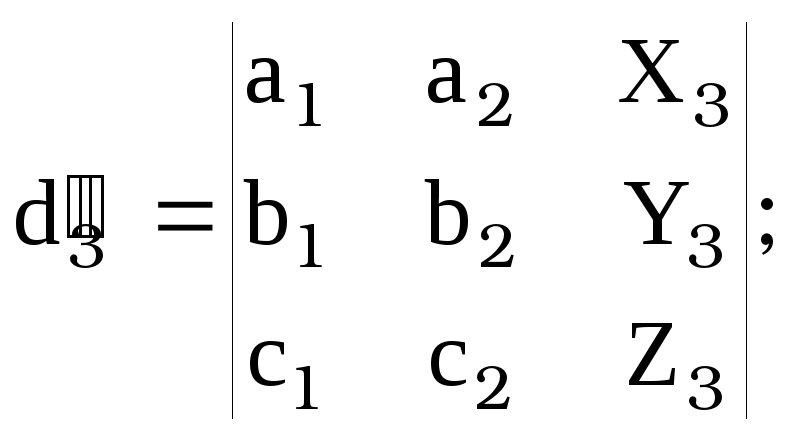
Итак, зная приближенно , из [13] находим значение (а из [12] ), которые определены из условия положения плоскости орбиты светила [4]. Однако нам неизвестны даже приближенные значения отношений площадей треугольников . Найдем их.