Перелік питань до іспиту з «Алгебри та геометрії» для студентів 1 курсу спец. «комп’ютерна інженерія» 2014-2015 н.Р.

1. Визначники порядку 2 та 3, їх властивості. Правило Крамера.

ычисление определителей II и III порядка

Определителем называется число, записанное в виде квадратной таблицы.Таблица ограничивается слева и справа вертикальными линиями.

Главная диагональ определителя содержит элементы aii, противоположная диагональ называется побочной.

Порядком определителя называется число строк (столбцов) квадратной таблицы.

Определитель II порядка вычисляется по формуле:

a1*b2--a2*b1

Определитель III порядка можно вычислить по правилу Сарруса:

a11 a12 a13 a11 a12

a21 a22 a23 a21 a22

a31 a32 a33 a31 a32

a13a22a31+a11a23a32+a12a21a33-a11a22a33-a12a23a31-a13a21a32

Основные свойства определителей:

1.1. Значение определителя не изменится, если:

- строки заменить на столбцы, такое действие называется транспонирование, т.е. действия, выполняемые со строками, справедливы и для столбцов;

- все элементы одной строки умножить на какое-либо число и прибавить к соответствующим элементам другой строки.

Такие действия с элементами определителя называются элементарными преобразованиями.

1.2. Определитель меняет знак на противоположный, если две каких-либо строки поменять местами.

1.3. Определитель равен нулю, если:

- все элементы какой-либо строки равны нулю;

- соответствующие элементы каких-либо двух строк равны;

- соответствующие элементы каких-либо двух строк пропорциональны.

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы.

Если определитель равен нулю , то система имеет бесконечно много решений или несовместна(не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если определитель не равен нулю то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:

Y и X

Их корни находим по принципу замены соответствующей переменной свободными членами.Затем XиYделим на главный определитель системы,получая координаты значения координат (x,y) из этого мы можем вычислить вектор.

2. Перестановки, їх кількість. Транспозиції, інверсії.

Пусть дано некоторое конечное множество N, состоящее из п элементов. Каждому из этих элементов может быть присвоен номер от 1 до п. В рассматриваемых в дальнейшем задачах свойства элементов множества N не будут существенны, и будем считать, что элементами множества служат сами числа 1, 2, ,п.

Перестановкой степенип называется упорядоченный набор (i₁,i₂,,i_n) п чисел 1,2,,п (или п различных элементов).

Число различных перестановок из п элементов равно произведению 12п, которое обозначается п! (читается “эн-факториал”). Действительно, в качестве i₁можно взять любой из п элементов (любое из чисел 12п), для чего можно выбрать п вариантов. Если элемент i₁ выбран, то в качестве i₂можно взять любой из оставшихся п – 1 элементов, то есть число различных вариантов выбора i₁, i₂ равноп(п –1) и т. д.

Если в некоторой перестановке поменять местами какие-либо два элемента, а все остальные элементы оставить на месте, то получится новая перестановка. Такое преобразование перестановки будем называть транспозицией.

Теорема. Все п! перестановок из п элементов можно расположить в таком порядке, что каждая следующая перестановка будет получаться из предыдущей одной транспозицией, причём начинать можно с любой перестановки.

Доказательство проведём по индукции. Утверждение, очевидно, справедливо при п = 2. Предположим, что утверждение справедливо при п – 1, и покажем, что тогда оно справедливо при п. Пусть задана изначальная перестановка i₁,i₂,,i_n. Рассмотрим все перестановки из п элементов, в которых на первом месте стоит i₁. Таких перестановок (п – 1)! их можно упорядочить любым способом с помощью конечного числа транспозиций, так как, согласно предположению индукции, доказываемое утверждение справедливо для числа элементов п – 1. В последней из полученных перестановок из п элементов поменяем местами элемент i₁с любым из остальных элементов, например, с i₂. Начиная с полученной перестановки, можно упорядочить любым способом все перестановки, у которых на первом месте стоит i₂. Действуя таким образом, можно перебрать все перестановки из п элементов.

Отсюда следует, что от любой перестановки из п элементов можно перейти к любой другой перестановке из тех же элементов при помощи конечного числа транспозиций.

Пусть элементами перестановки являются числа 1,2,,п..Числа iиj составляют инверсию в данной перестановке, если i > jи при этом i стоит в этой перестановке раньше j. Перестановка называется чётной, если она содержит чётное число инверсий и нечётной – в противоположном случае.

Теорема. Всякая транспозиция меняет чётность перестановки.

Доказательство. Сначала рассмотрим транспозицию двух рядом стоящих элементов. Если до транспозиции они составляли инверсию, то после неё инверсию они не составят, и наоборот, если до транспозиции между ними инверсии не было, то после транспозиции она появится. Очевидно, что число инверсий, которые рассматриваемые элементы составляли до транспозиции с элементами, стоящими до них и после них в перестановке при транспозиции не изменится. Таким, образом, чётность перестановки после транспозиции двух рядом стоящих элементов изменится. Пусть теперь первый из тех элементов перестановки, который будет “участвовать” в транспозиции (в дальнейшем будем называть его первым элементом), стоит на i-м месте в перестановке, а второй “участник транспозиции” (в дальнейшем называемый вторым элементом) занимает место с номером i + k. Чтобы поменять местами эти элементы будем действовать следующим образом. Сначала последовательно поменяем местами первый элемент с k – 1 элементами, стоящими между первым и вторым, так, что первый элемент станет соседним элементом слева для второго (тем самым проведём k – 1 транспозиций двух соседних элементов). Затем поменяем местами первый и второй элементы (ещё одна транспозиция двух соседних элементов). Теперь осталось поставить второй элемент на место первого, для чего опять нужно провести k – 1 транспозиций второго элемента с элементами, первоначально находившимися между первым и вторым. Таким образом, проведено 2(k – 1) + 1 транспозиций двух стоящих рядом элементов. Тем самым чётность перестановки была изменена нечётное количество раз, что и доказывает теорему.

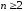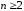При число чётных перестановок степенип равно числу нечётных, то есть равно п!/2. Действительно, все п! перестановок можно упорядочить так, что каждая последующая получается из предыдущей одной транспозицией. Таким образом, две соседние перестановки будут иметь противоположные чётности. Из того, что п! при – число чётное, следует справедливость утверждения.

Можно записать одну под другой две перестановки п-й степени, заключая полученные две строки в скобки, например при п = 5:

(1)

3. Підстановки п-ого степеня, їх кількість. Теорема про розклад транспозиції у транспозицію сусідніх.

Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.

Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ обозначает подстановку, в которой 3 переходит в 4, 1 2, 2  1, 4  3. Подстановка называется четной (илинечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде 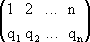,т.е. с натуральным расположением чисел в верхней строке.

Пусть нам дана квадратная матрица порядка n

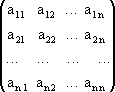                                    .                                                  (4.3)

Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:

                        ,                                                    (4.4)

где индексы q₁, q₂,..., q_n составляют некоторую перестановку из чисел 1, 2,..., n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (4.4) равен (- 1)^q, где q - число инверсий в перестановке вторых индексов элементов.

Определителем n -го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ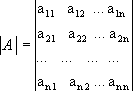или det A=(детерминант, или определитель, матрицы А).

4. Визначник порядку п. Властивості визначників.