termex / Theoretical_Mechanics_part_02_04

Статика

Краткий курс Теоретической Механики

39

§ 7. Произвольная система сил. 7.1. Основная лемма.

Всякая сила, приложенная к АТТ в данной точке A ,

эквивалентна той же силе, приложенной в другой точкеB , и паре сил, момент которой равен моменту силы, приложенной в точке A , относительно точки B .

Пусть в точке		A твердого тела приложена сила							FA .
Приложим к точке B две взаимно противоположные силы
FB и FB′ , равные по величине силе FA и параллельные
этой силе.
			FB			FA
		B				A
	FB′
Тогда	FA ~ (FA , FB , FB′			) .	Но	силы	FA	и	FB′
составляют	пару,	поэтому		имеем		FA ~ {FB ; (FA , FB′ )} ,
причем момент		пары	(FA , FB′		) будет равен			моменту
								r
данной силы FA относительно точки B , т.е.							BA × FA .
Лемма доказана.
7.2. Приведение пространственной системы сил.
Пусть	мы	имеем	произвольную				систему		сил

F1 , F2 , F3 ,K, Fn , действующих на АТТ и как угодно расположенных в пространстве.

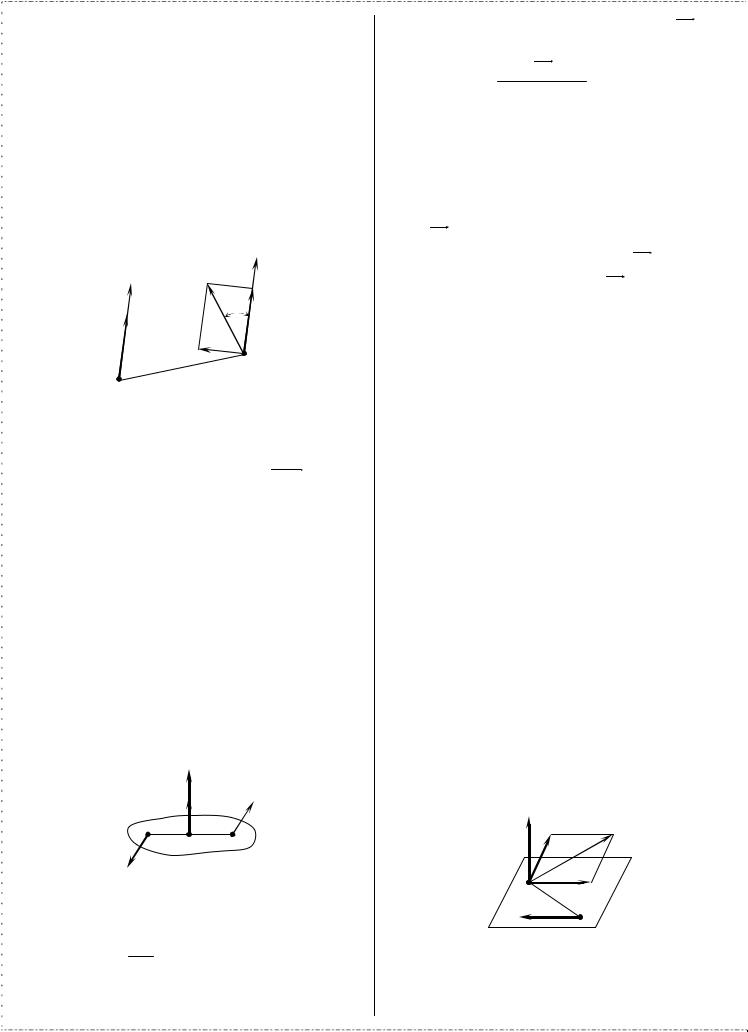
Выберем произвольный центр O и перенесем все силы системы в этот центр. От перенесения каждой силы мы получим силу и пару, момент которой равен моменту переносимой силы относительно выбранного центра O .

R		F1
Μo		F2
	r1	r2
O		Fn

rn

Складывая все силы в центре O , мы получим одну результирующую силу

r n r
R = ∑Fi .	(7.1)

i =1

Складывая моменты всех пар сил, получим вектормомент результирующей пары

r	n	r
Μo	= ∑(rri	× Fi ) .	(7.2)

i=1

Величина R , равная векторной сумме всех сил системы, называется главным вектором системы сил, а величина

Μo , равная векторной сумме моментов всех сил системы

относительно центра O , называется главным моментом системы сил относительно этого центра O .

7.3. Перемена центра приведения.

Пусть пространственная система сил приведена к центру O и заменена результирующей силой R и парой сил с моментом Μo , который с направлением R образует некоторый угол α.

Возьмем новый центр приведения O′. Поскольку вектормомент Μo есть свободный вектор, то мы переносим его в центр O′ без изменения направления и величины. Перенесение главного вектора R по основной лемме должно сопровождаться добавлением в точке O′ момента главного вектора R относительно нового центра O′.

Таким образом, в результате приведения системы векторов {R, Μo } к новому центру O′ мы имеем систему

векторов {R, Μo′} .

Следовательно, при изменении центра приведения главный вектор R системы сил не изменяется, а главный

		′		r	равную моменту
момент изменяется на величину O O × R ,
главного вектора R ,	приложенного			в	старом центре
приведения – O , относительно нового центра приведения –
O′, т.е.
α		Μo			Μo′
R		r
O
		OO′× R
				Μo
	R′
r	r	O′	r
		′
			× R	.	(7.3)
Μo′ = Μo + O O

7.4. Инварианты приведения.

Поскольку при изменении центра приведения главный

вектор системы сил R не изменяется, то он представляет собой инвариант пространственной системы сил по отношению к изменению центра приведения, т.е.

R′ = R .	(7.4)
Вторым инвариантом системы	будет скалярное

произведение главного вектора R на главный момент Μo , т.е. величина R Μo = R Μo cos α, или же проекция главного момента на направление главного вектора, т.е. величина Μo cos α , (поскольку R сам есть инвариант).

Покажем это.

Μo′

R′

Μo

R

α

O′

O

α

Для центра O′, из (7.3)-(7.4) имеем:

′

r

r

′

r

R

= R

и Μo′

= Μo

откуда

r′

+ O O × R ,

′

r

r

r

′

r

r r

r

r

R

Μo′

= R

(Μo + O O

× R) =

R Μo

+

R (O O × R) .

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

2 апреля 2007 г.

Статика

Краткий курс Теоретической Механики

40

Но второй член правой части равен нулю, следовательно,

R′ Μo′ = R Μo = const или Μo cos α = const . (7.5)

7.5. Приведение системы сил к динаме.

Если центр приведения O выбран произвольно, то главный вектор R и главный момент Μo системы сил будут составлять между собой некоторый угол α.

Разложим главный момент Μo на две составляющие: составляющую ΜR , направленную вдоль главного вектора

R , и составляющую Μ , перпендикулярную к главному вектору R . Таким образом, Μo = ΜR + Μ .

r

R

Μo R

α ΜR

ΜR

Μ

O

O*

Вектор ΜR , как коллинеарная составляющая главного момента Μo по направлению главного вектора R , есть для

	данной системы сил величина постоянная и не зависящая от
							r
	выбора центра		приведения, т.е. ΜR = const ,					причем
	численно					r r
	Μ	R	= Μ	o	cos α =	R Μo	= const .	(7.6)
						R

Таким образом, с изменением центра приведения будет изменяться только перпендикулярная составляющая Μ .

Мы всегда сможем найти такой центр приведения O* , чтобы переменная составляющая Μ обратилась в нуль.

Тогда главный момент Μo и главный вектор R будут направлены по одной прямой, т.е. будут коллинеарными, а вектор Μo будет минимален по величине и равен ΜR .

Совокупность силы и пары сил, вектор-момент которой коллинеарен силе, или, что то же, совокупность силы и пары, лежащей в плоскости, перпендикулярной силе, носит название динамы или динамического винта.

r

Μ

R	r
	F

r	O*
F′

Центр O* , при приведении к которому система сил заменяется динамой, можно аналитически определять из условия, что для этого центра ΜR ↑↑ R , т.е.

	r		r	r
	ΜR	= p =	R Μo		,	(7.7)
	r
			R2
	R

где p – постоянная линейная величина, называемая

параметром винта.

			r	r	r
Так как, согласно равенству (7.3) ΜR				= Μo	− OO* × R ,
то уравнение (7.7) можно переписать в виде
r		r
M	o	− OO* × R	= p .		(7.8)
		r

R

Этому уравнению удовлетворяет бесконечное множество точек, лежащих на общем направлении векторов

R и ΜR . Следовательно, уравнение (7.8) есть уравнение

прямой, которую называют центральной осью системы сил.

Равенство (7.8) выражает уравнение центральной оси в векторной форме, причем текущей координатой является

вектор OO* .

Если координаты векторов R , Μo , OO* обозначить

R(Rx , Ry , Rz ) , Μo (Μx , Μy , Μz ) , OO* (x* , y* , z* ) , то в

проекциях на оси координат уравнение центральной оси примет вид

Μx − (y* Rz − z* Ry )		=	Μy − (z* Rx − x* Rz )		=
Rx				Ry		(7.9)
	Μz − (x* Ry − y* Rx )
=				= p.

Rz

Итак, всякая система сил, действующих на АТТ, для

которой второй инвариант R Μ не равен нулю,

приводится к динаме, которую образуют главный вектор R , направленный по центральной оси системы, и пара сил с моментом ΜR .

7.6. Приведение системы к двум силам.

Покажем, что всякую систему сил, действующих на АТТ, для которой второй инвариант не равен нулю

R Μo ≠ 0 , еще можно привести к двум силам, одна из которых проходит через заданную точку O .

Приведем систему к центру O . Тогда получим в центре

O результирующую силу, равную главному вектору R , и результирующую пару с моментом, равным главному

моменту Μo .

Представим Mo в виде пары сил (F, F′) , одна из которых F проходит через точку O . Тогда вся система приведется к двум силам: Q = R + F и F′ , которые будут

лежать в разных плоскостях, причем сила Q будет проходить через заданную точку O .

Μo R	Q
O	F
F′

Если же Μo R , т.е. Μo R = 0 , то R будет лежать в плоскости пары (F, F′) , и, следовательно, силы Q и F′

будут лежать в одной плоскости, а вся система сил приведется к одной силе – равнодействующей.

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

2 апреля 2007 г.

Статика

Краткий курс Теоретической Механики

41

Если же при этом R = 0 , то, очевидно, что вся система приведется к паре сил.

7.7. Случаи приведения.

Выше мы показали, что всякая система сил, приложенных к АТТ, при приведении к данному центру

заменяется результирующей силой R , равной главному вектору системы, и результирующей парой с моментом

Μo , равным	главному	моменту	системы относительно
		r
этого центра.	Векторы	R и Μo	называются элементами

приведения системы. Их значения определяются формулами (7.1) и (7.2), или вытекающими из этих формул равенствами

n

Rx = ∑Fix , i=1

n

Ry = ∑Fiy , i=1

n

Rz = ∑Fiz, i=1

n	r
Μx = ∑momx	(Fi ),
i=1
n	r
			(7.10)
Μy = ∑momy (Fi ),
i=1
n	r
Μz = ∑momz (Fi ).
i=1

В зависимости от значения инвариантов системы и элементов приведения можно различать следующие случаи приведения системы сил.

1.) R Μ ≠ 0 .

Система приводится к динаме {R, ΜR } с параметром

r	r					лежащим в разных
p = ( R Μ) / R2 , или к двум силам,
плоскостях.
2.) R Μ = 0 .
Здесь возможны следующие частные результаты:
А)	Если R ≠ 0 ,		то	система		сил	приводится		к
равнодействующей, равной главному вектору R .
Это вытекает из того,			что при R Μ = 0 будет					p = 0 и,
согласно		равенству	(7.7),		ΜR = 0 .		Следовательно,
динама		вырождается		в	одну	силу		R ,	т.е.

равнодействующую. При этом линия действия R совпадает с центральной осью системы (которая задается уравнениями (7.9), если в них положить p = 0 ). Если

одновременно и Μ = 0 , то равнодействующая будет, очевидно, проходить через центр приведения O .

Если же Μ ≠ 0 , то равнодействующая R проходит через некоторый другой центр O* . Таким образом, для

того, чтобы система сил имела равнодействующую, необходимо и достаточно выполнения двух условий

R ≠ 0 и R Μ = 0 для любого центра приведения.

Б) Если R = 0 , но Μ ≠ 0 , то при этом, как видно из (7.3), Μo′ = Μo , т.е. главный момент не зависит от выбора центра приведения. Система приводится в этом случае к паре сил с моментом Μr o = ∑momo (Fi ) ,

где O есть произвольный центр.

В) Если R = 0 и Μ = 0 , то система сил эквивалентна нулю, т.е. находится в равновесии.

Теорема Вариньона. Если система сил имеет

равнодействующую, то момент этой равнодействующей относительно произвольного центра равен сумме моментов всех сил системы относительно того же центра.

Пусть некоторая система сил F1 , F2 ,..., Fn имеет

равнодействующую	R , приложенную	в	точке	C .
Перенесем R в	произвольную точку	O .	При	этом
	r		r
добавится пара (R, R′′) с моментом Μ = momo (R) .

С другой стороны, Μ есть главный момент системы относительно центра O и равен сумме моментов всех сил

относительно этого центра, т.е. Μr = ∑momo (Fri ) .

	R′′		Μo
C		O	R′

R

Сравнивая между собой эти равенства, получаем теорему Вариньона

r	r
momo (R) = ∑momo (Fi ) .		(7.11)

Проектируя обе части равенства (7.11) на любую ось, проходящую через центр O , найдем, что теорема Вариньона справедлива и для моментов относительно оси.

Для заметок

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

2 апреля 2007 г.