termex / Theoretical_Mechanics_part_01_04

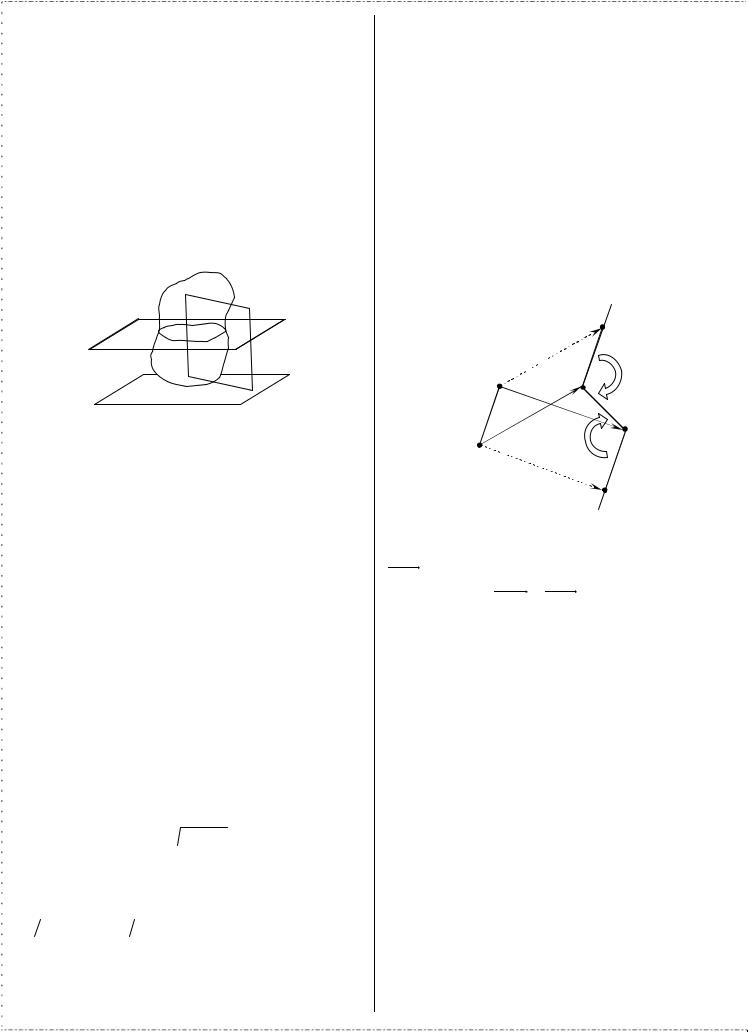
Кинематика

Краткий курс Теоретической Механики

12

§4. Плоскопараллельное (плоское) движение АТТ

4.1.Основные понятия. Плоскопараллельным

движением АТТ называется такое его движение, при котором

все точки тела движутся параллельно какой-нибудь неподвижной плоскости π. При этом произвольная прямая

АВ, неизменно скрепленная с телом и перпендикулярная к основной плоскости π, будет двигаться поступательно, т.е. параллельно самой себе.

Следовательно, движение точек тела, лежащих на этой прямой, определяется движением одной из этих точек, а движение всего тела – движением параллельного основной плоскости π сечения S тела в плоскости этого сечения.

Таким образом, изучение плоского движения тела сводится к рассмотрению движения плоской неизменяемой фигуры (ПФ) в ее плоскости.

	A	A′
		S
	B	B′
π

Неизменяемой будем называть такую плоскую фигуру, у которой расстояние между любыми двумя точками остается неизменным со временем (т.е. при движении).

Положение ПФ в ее плоскости однозначно определяется положением двух произвольных точек этой фигуры (положением отрезка прямой, соединяющего эти точки).

В дальнейшем мы будем рассматривать движение всей подвижной плоскости, неизменно связанной с движущейся фигурой, относительно неподвижной и параллельной ей основной плоскости π.

Основными видами движения ПФ в ее плоскости являются поступательное и вращательное движения.

Поступательным движением ПФ в ее плоскости будет такое движение, при котором любая прямая, взятая в плоскости фигуры, перемещается параллельно самой себе. Все точки ПФ при этом имеют равные скорости и ускорения и описывают конгруэнтные траектории.

Вращательным движением ПФ в ее плоскости будет такое движение, при котором одна точка, называемая центром вращения, остается неподвижной, а остальные точки фигуры движутся по концентрическим окружностям вокруг центра вращения.

При вращательном движении скорости и ускорения точек ПФ пропорциональны их расстояниям R до центра

вращения: v = ωR, w = R ε2 + ω4 , где ω и ε – угловая скорость и угловое ускорение вращения.

Ускорение точки ПФ при вращательном движении отклонено от радиуса вращения R на угол α, который одинаков для всех точек, поскольку wτ wn = tg(α) = ε ω2 .

Полюсом мы будем называть некоторую точку в плоскости движения ПФ, неизменно связанную с этой фигурой.

4.2. Геометрическая картина движения ПФ.

Теорема 1. Всякое перемещение плоской фигуры в ее плоскости может быть составлено из поступательного перемещения и поворота около произвольно выбранной точки (полюса). При этом поступательная часть перемещения зависит от выбора полюса, а вращательная часть – не зависит.

Пусть имеем два произвольных положения П1 и П2 плоской фигуры П , характеризуемые положениями А1В1

иА2В2 отрезка АВ, неизменно связанного с этой

фигурой. Выберем в качестве полюса точку A и поступательным перемещением фигуры П совместим

точки	А1 и А2 . При этом отрезок АВ займет положение
А2В2′	, причем А1В1 ||	А2В2′ . При повороте фигуры около
центра	А2 на угол ϕ	отрезок А2В2′ займет положение
А2В2 , а фигура П – требуемое положение П2 .
		B2′
	B1	ϕ
		A2

ψ B2

A1

A2′

Если в качестве полюса взять другую точку – точку B , то из положения П1 в П2 фигура будет переведена

поступательным перемещением, определяемым вектором В1В2 и поворотом вокруг полюса B на угол ψ .

Очевидно, что А1 А2 ≠ В1В2 , т.е. поступательная часть перемещения с изменением полюса меняется.

Углы поворота ϕ и ψ равны, как накрест лежащие, а

направления поворотов совпадают. Следовательно, вращательная часть движения плоской фигуры от выбора полюса не зависит.

Поскольку поступательная часть перемещения ПФ с изменением полюса изменяется, оказывается возможным выбрать полюс так, чтобы эта часть перемещения вообще отсутствовала.

Теорема 2. Всякое непоступательное перемещение плоской фигуры в ее плоскости может быть выполнено одним поворотом фигуры около определенного центра, называемого центром конечного вращения.

Пусть имеем два произвольных положения П1 и П2 плоской фигуры П , характеризуемых положениями А1В1

иА2В2 отрезка АВ, неизменно связанного с этой

фигурой, причем, согласно условиям теоремы,

А1В1 |/| А2В2 .

Если центр конечного вращения существует, то он должен находиться в такой точке O , которая была бы равноудалена от А1 и А2 , а также от B1 и B2 , т.к.

должно быть OА1 = OA2 и OB1 = OB2 .

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

27 февраля 2007 г.

Кинематика Краткий курс Теоретической Механики 13

A2

Из доказанных теорем следует также, что поворот вокруг

B1

любого полюса или вокруг мгновенного центра происходит с

одной и той же для данного момента времени угловой

скоростью ω. Величина ω, не зависящая от выбора полюса,

ϕ

ϕ

B2

называется угловой скоростью фигуры в

данный момент

A1

времени или мгновенной угловой скоростью.

O

4.3. Мгновенный центр вращения. Мгновенный центр

Следовательно,

центр

вращения

должен

находиться

в

вращения (МЦВ) получается как предельное положение

центра конечного вращения

O ,

когда

положение

П

точке

пересечения

перпендикуляров,

восстановленных

из

2

фигуры

неограниченно приближается к

П . Этот

центр

середин отрезков A1 A2 и B1B2 . Докажем,

что точка

O

1

представляет собой точку, элементарным поворотом вокруг

действительно есть центр вращения.

которой плоская фигура перемещается из данного положения

Поскольку

А1O = A2O ,

B1O = B2O

и

в бесконечно близкое, соседнее ему положение.

А1OA2 = B1OB2 ,

то

при

повороте

фигуры

на угол

r

А OA

= ϕ отрезок

совпадет с

и фигура

A B

A B

A

vn−1

1

2

1 1

2 2

n−1

A3

из положения П1 перейдет в положение П2 .

v

r

1

Равенство

углов

А1OA2 = B1OB2

легко

доказать

r

v2

r

следующими

рассуждениями.

Из

равенства

сторон

A

v3

An

А1B1 = A2 B2 ,

OА1 = OA2 ,

OB1 = OB2

следует

P

2

равенство

треугольников

A1B1O и

A2B2O ,

откуда

A1

r

имеем равенство А OB

= А OB .

vn

1

1

2

2

Прибавив к обеим частям последнего равенства по углу

B1OA2 , получим: А1OA2 = B1OB2 =

ϕ. При этом

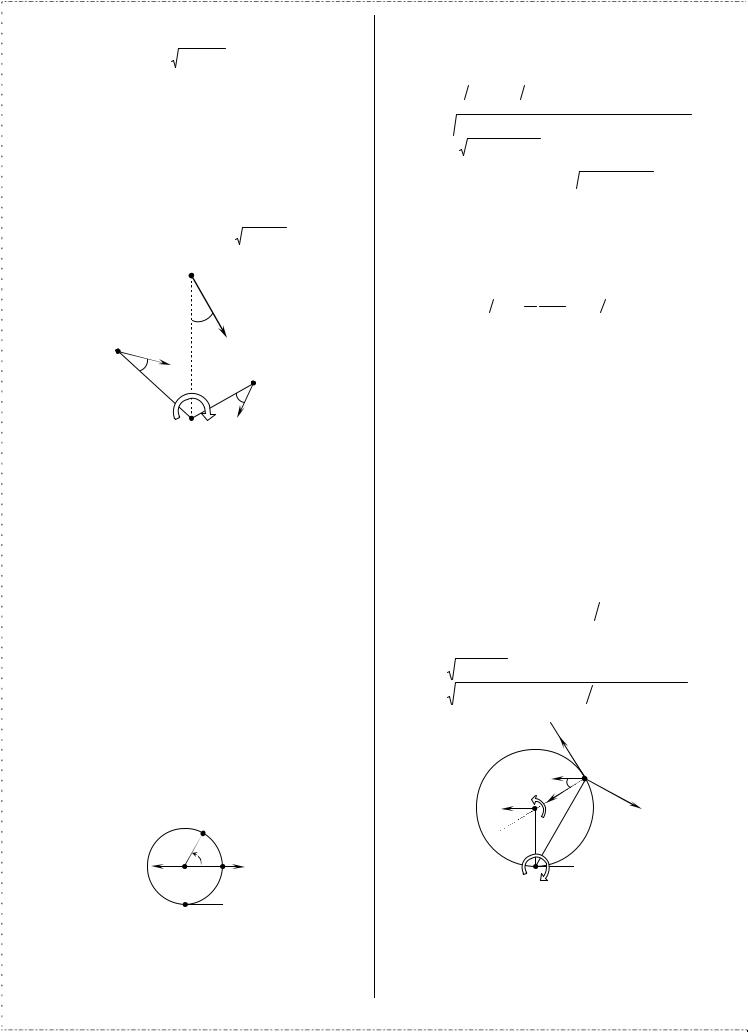
Скорости всех точек A1,..., An плоской фигуры будут в

легко видеть, что угол

ϕ равен углу между направлениями

данный момент времени перпендикулярны к радиусам

отрезков

A B

и

A B ,

т.е.

остается таким же,

как при

вращения

PAi , соединяющим мгновенный центр

P с

1

1

2

2

этими точками.

повороте вокруг любого полюса по теореме 1.

Доказанные теоремы дают представления о двух

Скорость точки плоской фигуры, совпадающей с

возможных способах перемещения плоской фигуры из

центром P , будет в данный момент равна нулю; эту точку

одного ее фиксированного положения в другое, а также

фигуры называют мгновенным центром скоростей.

раскрывают геометрическую картину движения плоской

Зная положение мгновенного центра P ,

можно, найти в

фигуры в ее плоскости.

данный момент времени направление скорости любой точки

Всякое движение непрерывно и может рассматриваться

ПФ. Так как перпендикуляры

PAi

к

направлениям

как

непрерывная

последовательность

элементарных

скоростей v всех точек плоской фигуры,

восставленные из

перемещений:

i

этих точек, пересекаются в данный момент в центре

P , то

•

Согласно теореме 1 любое элементарное перемещение

для определения положения мгновенного центра

можно

получить

путем

бесконечно

малого

вращения надо знать направления скоростей каких-

поступательного перемещения вместе с произвольно

нибудь двух точек фигуры. Восставив из этих точек

выбранным полюсом и поворота на бесконечно малый

перпендикуляры к направлениям их скоростей, получим в

угол вокруг этого полюса.

точке пересечения этих перпендикуляров мгновенный центр

Отсюда вытекает, что всякое движение плоской фигуры в

вращения P .

ее плоскости можно рассматривать как совокупность

Геометрическую картину движения плоской фигуры в ее

плоскости можно еще представить с помощью так

поступательного движения, определяемого движением

произвольно

выбранного

полюса,

и

вращательного

называемых центроид. При движении ПФ положение МЦВ

движения вокруг этого полюса;

будет непрерывно изменяться как на неподвижной плоскости,

так и на плоскости, неизменно связанной с движущейся

•

Согласно

теореме 2

любое

непоступательное

фигурой.

элементарное перемещение фигуры можно осуществить

Геометрическое место мгновенных центров вращения на

одним только поворотом на бесконечно малый угол

неподвижной плоскости есть непрерывная кривая, которая

вокруг определенного центра, называемого мгновенным

называется неподвижной центроидой. Геометрическое

центром вращения.

место мгновенных центров вращения на подвижной

Отсюда вытекает, что всякое непоступательное

плоскости, неизменно связанной с движущейся ПФ, есть

движение плоской фигуры в ее плоскости можно

также непрерывная кривая, называемая подвижной

рассматривать

как

непрерывную

последовательность

центроидой.

бесконечно малых поворотов вокруг мгновенных центров

В каждый момент времени обе центроиды будут касаться

вращения.

друг друга в мгновенном центре вращения, соответствующем

При этом положение мгновенного центра вращения

этому моменту времени.

непрерывно изменяется как в неподвижной плоскости,

После элементарного поворота ПФ вокруг данного

так и в плоскости фигуры.

мгновенного центра, подвижная центроида, повернувшись

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

27 февраля 2007 г.

Кинематика

Краткий курс Теоретической Механики

14

вместе с этой фигурой, соприкоснется с неподвижной центроидой в новой точке, которая будет мгновенным центром вращения для следующего момента времени и т.д.

Следовательно, при движении ПФ подвижная центроида катится по неподвижной центроиде без проскальзывания (точка касания, являющаяся МЦВ, имеет скорость, равную нулю). Так, например, если круг D , катится без скольжения по прямой Ox , то окружность этого круга будет подвижной

	центроидой, а	ось	Ox	–		D
	неподвижной	центроидой.
	Мгновенный центр вращения будет O					x
	в точке P касания обеих центроид.					P
	4.4. Скорости	точек	плоской

фигуры. Пусть плоская фигура движется по отношению к основной системе отсчета Oxy , в которой положение

полюса A и произвольной точки M определяются соответственно радиус-векторами rM и rA .

y

A AM

rM

rA	r
	rM
O	x

Тогда в любой момент времени для векторов rA , rM и

rr = AM справедливо векторное равенство rM = rA + r ,

дифференцируя по времени обе части которого, будем иметь: rr&M = rr&A + rr& .

Но так как | AM |= const , то вектор r изменяется при

движении фигуры только по направлению. Следовательно, для него справедлива формула (3.15):

			r	r	r
		r&		= ω× r .
Кроме того, rr&		= vr	, а rr&		= vr		, и мы получаем:
	M	M		A		A
r	r	r				vM = vA + vMA .			(4.1)
vM	= vA + ω× AM или
				r
				vMA		r
						vM
				ω
	A				M			r
		r						vA
		vA
Таким образом, вектор скорости vM данной точки M
плоской фигуры есть сумма:					вектора			vA – скорости
произвольно выбранного полюса						A , (общей для всех точек
фигуры);	и скорости			r		r
				vMA	= ω× AM , происходящей
вследствие вращения фигуры вокруг полюса A .
Вектор vMA направлен перпендикулярно вектору									AM
в сторону	вращения		фигуры,			а	по	модулю	равен

vMA = ω AM .

Полученный результат позволяет найти скорость любой

точки фигуры, если известны скорость какой-нибудь одной r

ее точки A и угловая скорость фигуры ω. Другие способы определения скоростей точек плоской фигуры вытекают из рассматриваемых ниже теорем.

Теорема І. Если известны скорость какой-либо точки

фигуры и направление скорости другой ее точки, то можно определить скорость любой точки плоскости этой фигуры с помощью мгновенного центра вращения.

Пусть даны скорость точки A и направление скорости точки B . По известным направлениям скоростей в точках

Aи B строим мгновенный центр вращения P .

Тогда из равенства vA = ω PA находим мгновенную

угловую скорость вращения ПФ

ω = vA PA ,

(4.2)

и скорость произвольной точки M фигуры в этот момент времени:

vM = vA	PM	и vrM PM .	(4.3)
	PA

Ar

vA

M

r vM

ω

P

B

Равенство (4.3) показывает, что в каждый момент времени скорости всех точек плоской фигуры пропорциональны их расстояниям до мгновенного центра вращения.

Если направления заданных скоростей vA и vB будут

между собой параллельны, то доказанная теорема теряет силу. При этом может иметь место один из случаев:

а) vrA || vrB , но точки A и B не лежат на общем перпендикуляре к vA . В этом случае мгновенный центр P бесконечно удален от ПФ и равенство (4.2) дает ω = 0 .

Тогда из формулы (4.1) следует, что скорость любой точки M плоской фигуры vM = vA , т.е. имеет место

мгновенно-поступательное распределение скоростей.

	M	A
		B
		r
	vM	vA
б) vrA || vrB , а	точки	A и B лежат на общем
перпендикуляре к	AB . В этом случае перпендикуляры AP

и BP к векторам vA и vB сливаются и для определения

положения точки P надо дополнительно знать модули обеих скоростей.

Тогда, согласно (4.3), будет vA AP = vB BP , и точка P найдется как пересечение прямой, соединяющей концы

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

27 февраля 2007 г.

Кинематика

Краткий курс Теоретической Механики

15

векторов, изображающих скорости vA и vB , с прямой

AB . Следовательно, в случае б) для нахождения скорости vM любой точки M фигуры надо знать и модули, и

направления скоростей обеих точек A и B .

r

A vA

r

B vB

ω

P

Если, в частности, будет vA = vB , то опять имеет место

мгновенное поступательное распределение скоростей и для любой точки ПФ будет v = vA .

Теорема II. Проекции скоростей концов неизменяемого отрезка на его направление равны между собой.

Доказательство этой теоремы базируется на формуле (4.1). Умножим скалярно обе части этого равенства на

вектор	AM .	Тогда		r	= 0 , поскольку
			AM (ω× AM)
r		Сокращая на		длину	отрезка AM ,
AM (ω× AM) .
окончательно получим
	vM cos(μ) = vA cos(α) ,				(4.4)
где α и	μ углы, которые составляют векторы скоростей
vA и vM точек A и M с отрезком AM .
			r
			vM	r
				μ vMA
			ω
	A	α	M	r
		r		vA

vA

4.5.Ускорения точек ПФ. Дифференцируя обе части формулы (4.1) по времени, получим

r

r

r

r

r

r

dv

M

dv

A

dω

dr

=

+

×r

+ ω×

.

(4.5)

dt

dt

dt

dt

Величина

r&

r

ω = ε есть вектор углового ускорения ПФ.

Этот

вектор

направлен

перпендикулярно

к плоскости

r

r

r

&

фигуры также как и вектор ω. Причем ε ↑↑ ω, если

ω > 0 ,

r

r

&

что

ω r и ω r = 0 ,

и ε ↓↑ ω, если

ω < 0 . Учитывая,

преобразуем последнее слагаемое в (4.5):

r r

r

r r

r r r

r r r

r

. (4.6)

ω×r&

= ω×

(ω×r) = ω

(ω

r)

− r (ω ω) = −ω2r

Введем обозначения

r

r

rвр

,

2 r

r

цс

(4.7)

ε ×r = wМА

− ω

r

= wMA .

Векторы

r

и

r

представляют

собой

wвр

wцс

МА

MA

вращательное и центростремительное ускорения точки

M по отношению к полюсу A , так если бы фигура совершала только вращение вокруг этого полюса.

Окончательно запишем:

r		r		r	вр		r	цс
w	M	= w	A	+ w	MA		+ w	MA
или	wM = wA + wМА .								(4.8)
		wM						r	вр
								w	MA
				r					w A
				wMA			μ
									M
w A					r	цс
					wMA

A ω ε

Таким образом, полное ускорение любой точки плоской фигуры складывается геометрически из ускорения полюса

wA и ускорения wrМА = wrMAвр + wrMAцс , которое получает точка при вращении вокруг этого полюса.

Численно эти составляющие равны:

	wМАвр = AM ε, wМАцс = AM ω2,	(4.9)
	wМА = AM ε2 + ω4 .

Угол μ, который составляет вектор ускорения wMA с

радиусом MA , определяется из равенства:

tg(μ) = wМАвр wМАцс = ε ω2 .

(4.10)

4.6. Мгновенный центр ускорений.

При непоступательном движении плоской фигуры в ее плоскости в каждый момент времени существует точка, ускорение которой в этот момент времени равно нулю. Эта точка называется мгновенным центром ускорений.

Рассмотрим алгоритм определения положения мгновенного центра ускорений по отношению к плоской фигуре (т.е. в плоскости движения этой фигуры).

	r	вр
	w	QA		r
r				w A
wQA	μ			Q
	r		цс
ε	w		QA
A	μ	wr A

Пусть нам известны ускорение wA точки A , а также угловая скорость ω и ускорение ε фигуры. Вычислим величину tg(μ) из равенства (4.10) и проведем под углом μ к вектору wA луч, который должен быть отклонен от wA в сторону вращения фигуры, если это вращение ускоренное

r	r	или против вращения, если	оно замедленное
( ε ↑↑ ω),
r	r	Отложим на луче отрезок AQ	, равный
( ε ↓↑ ω).
		AQ = wA ε2 + ω4 .	(4.11)

Точка Q и будет мгновенным центром ускорений (МЦУ). Докажем последнее утверждение.

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

27 февраля 2007 г.

wrMCцс

Кинематика

Краткий курс Теоретической Механики

16

Так как	r	r	r
	wQ = wA		+ wQA ,
где	w = AQ ε2		+ ω4 = w	A	,
	QA

и вектор wrQ должен составлять угол μ с прямой AQ , то вектор wQA параллелен wA и направлен в противоположную сторону, т.е. wQA = −wA .

r r r

Поэтому wQ = wA + wQA = 0 .

Если же МЦУ принять в данный момент времени за полюс, то, так как wQ = 0 , будем иметь из (4.8):

r	r	и wM = MQ ε2 + ω4 .
wM	= wMQ
		B
			r
			wB
			μ
	A	r
		w A
		μ	M
			ε
			μ
			r
		Q	wM

Следовательно, ускорения всех точек ПФ пропорциональны в данный момент времени их расстояниям до МЦУ. Кроме того, углы, которые образуют векторы ускорений с отрезками, соединяющими их точки с МЦУ, одинаковы и равны μ.

Следует отметить, что мгновенный центр скоростей P и мгновенный центр ускорений Q – это разные точки. Так

для точки фигуры, совпадающей с МЦС по определению vP = 0 , но wP ≠ 0 . Для точки фигуры, совпадающей с

МЦУ по определению wP = 0 , однако vP ≠ 0 .

Если же плоская фигура совершает чисто вращательное движение (около неподвижного центра O ), то мгновенный центр скоростей и мгновенный центр ускорений совпадают с неподвижным центром O вращения фигуры.

Теоретический пример.

Пусть круг, радиус которого равен R , катится без скольжения по прямолинейному рельсу. При этом его центр

C имеет в данный момент				времени скорость vC и
ускорение wC , изображенные на рисунке.
				M
				φ A
	r		C	r
	wC			vC

P

Найти скорость и ускорение произвольной точки M обода колеса, положение которой определяется углом φ ,

отсчитываемом от радиуса CA .

Решение. Поскольку точка P касания круга и рельса есть МЦС, то выбирая эту точку в качестве полюса, воспользуемся для определения скорости точки M

формулами (4.2) и (4.3):

ω = vC CP = vC R – угловая скорость колеса,

PM = CP2 + CM2 − 2 CP CM cos(90o + φ) = = R 2 (1 + sin φ),

vM = PM ω = vc 2 (1 + sin φ) .

Вектор скорости vM направим перпендикулярно отрезку PM в сторону мгновенного вращения ω круга вокруг своего МЦС.

Поскольку в любой момент времени R = const , то дифференцируя по времени формулу для угловой скорости

получим:	ε = dω dt = 1 dvC = w R .
	R	dt	C

Поскольку центр круга C движется прямолинейно, а его скорость vC и ускорение wC направлены в

противоположные стороны, то мгновенное вращение круга вокруг МЦС является замедленным. Поэтому направления ω и ε также будут противоположными.

Для определения ускорения точки M воспользуемся формулами (4.8)–(4.9):

wMCвр = ε R = wC , wMCцс = ω2 R = vC2 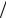R .

После того как по правилу (4.8) векторы wC , wrMCвр и

построены в точке M , спроектируем это векторное равенство на направления (1) и (2), что соответствуют направлениям векторов wrMCвр и wrMCцс :

w = wвр

+ w

C

sin φ = w

(1 + sin φ),

1

MC

C

w

= wцс

+ w

C

cos φ = v2

R + w

cos φ.

2

MC

C

C

Тогда, поскольку w1 w2 , получим окончательно:

w

M

=

w2

+ w2 =

1

2

.

=

w2

(1 + sin φ)2 + [v2

R + w

cos φ]2

C

C

C

(1)

r

вр

w

MC

r

wC

M

r

φ

wC

vM

r

цс

C

w

MC

ε

(2)

P

ω

Для заметок

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

27 февраля 2007 г.