termex / Theoretical_Mechanics_part_01_08

Кинематика

Краткий курс Теоретической Механики

27

§ 8. Сложное движение точки

r

~r

vra

=

dr

и vrr =

dr

.

dt

8.1. Основные понятия.

dt

Переносная скорость ve точки

M есть скорость той

Пусть

точка

M движется

относительно

некоторой

подвижной системы отсчета Oxyz , которая в свою очередь

неизменно связанной с триэдром Oxyz точки пространства

перемещается по отношению к основной (неподвижной)

M′, в которой в данный момент находится точка M .

системе

Ωξηζ .

Тогда движение, скорость и

ускорение

Тогда по формуле Эйлера ve = ω×r и

точки, рассматриваемые

по

отношению

к

подвижной

r

~r

r

r

системе

Oxyz ,

называются

относительными, а

по

dr

dr

=

+ ω× r

или

va

= vr + ve .

(8.1)

dt

dt

отношению к системе Ωξηζ – абсолютными.

Движение подвижной системы Oxyz по отношению к

Приведем

другое

доказательство

справедливости

формулы (8.1). Пусть i, j, k

суть единичные координатные

неподвижной

Ωξηζ

является для движущейся точки

M

переносным движением.

векторы подвижного триэдра Oxyz , тогда

Скорость и ускорение той неизменно связанной с

rr = rxi + ry j + rzk .

подвижной

системой

отсчета

Oxyz

точки пространства

Дифференцируя по времени, получим:

M′, в которой в данный момент находится движущаяся

r

r

drr

dr

dry r

r

r

точка M , называются переносными.

r

dr

di

dj

dk

=

x

i

+

j +

z

k

+

r

+ r

+ r

,

Другими словами,

переносную скорость и переносное

dt

dt

dt

dt

dt

dt

x dt

y

z

ускорение

точки

M можно

в

каждый момент времени

где

первые

три

члена

дают

локальную

производную

представить себе как ту скорость и то ускорение, которые

движущаяся точка M имела бы в данный момент, если она

~r

r

r

r

dr

начиная с этого момента оказалась бы жестко связанной с

= r&xi

+ r&y j

+ r&zk ,

так

как

они

представляют

собой

dt

подвижной

системой

Oxyz

(т.е.

не

совершала

бы

производную

вектора

r

при

условии,

что

i, j, k

относительного движения).

постоянны.

8.2. Полная и относительная производные от вектора.

Производные единичных векторов есть скорости их

Пусть подвижная

Oxyz и неподвижная

Ωξηζ системы

концов, т.е. скорости точек неизменяемой системы, которой

r

является

триэдр

Oxyz ,

тогда

по

формуле

Эйлера

отсчета имеют общее начало O , и пусть ω есть мгновенная

r

r

r

r

r

r

r

r

r

угловая скорость подвижной системыOxyz по отношению

&

&

&

и окончательно

i = ω× i,

j

= ω× j,

k

= ω× k

к неподвижной.

dr

dr

r

r

r

r

dr

r

r

r

=

~r

+ ω× (rxi + ry j + rzk) =

~r

+ ω× r.

Рассмотрим

точку

M ,

совершающую

движение,

dt

dt

dt

которое не зависит от движения триэдра Oxyz . Ее радиус-

Заметим, что формула (8.1) сохраняет свой вид и тогда,

вектор r

будет, очевидно, с течением времени изменяться в

когда трехгранник Oxyz ,

кроме вращения вокруг точки O ,

каждой из систем отсчета по разным законам.

совершает еще и поступательное движение, т.е.

ζ

z

M

перемещается как свободное твердое тело.

В этом случае единичные векторы

i, j, k

осей триэдра

ω

r

y

Oxyz

не изменяются и формулы

r&

r

r

,

r&

r

r

i

= ω× i

j

= ω× j ,

η

r&

r

r

сохраняют свой вид.

O

k = ω× k

Рассмотрим частные случаи:

r

~r

ξ

r

dr

dr

1.

система Oxyz неподвижна, тогда ω =

0,

=

;

x

dt

dt

2.

вектор

r

неподвижен по отношению к Oζηζ , тогда

Тогда за промежуток времени ∆t

вектор r

получит по

r

~r

отношению к осям Oξηζ

и

Oxyz

разные приращения,

dr

dr

r

r

~ r

= 0 и

= −ω×r

;

которые мы соответственно обозначим через ∆r

dt

dt

и ∆r .

3.

вектор

r

неизменно

связан

с

триэдром

Oxyz ,

тогда

Пределы отношений ∆r

~ r

→ 0 дадут

и ∆r к ∆t при ∆t

~r

r

r

r

соответственно производные

dr

dr

,

т.е.

скорость

конца

вектора

= 0,

= ω× r

r

~r

~ r

dt

dt

r

r

dr

=

lim

∆r

и

dr

=

lim

∆r .

определяется в этом случае как скорость точки АТТ,

dt

∆t→0 dt

dt

∆t→0 dt

«скрепленного» с подвижным триэдром Oxyz .

Производную

dr dt

будем

называть

«абсолютной»

8.3. Теорема о сложении ускорений.

или «полной», а производную

~r

dr dt «относительной»

Пусть

система

Oxyz

движется

относительно

или «локальной», причем из определений относительной

неподвижной системы Ωζηζ как свободное твердое тело.

vr и абсолютной va

скоростей следует, что

Обозначим через vo

и wo

скорость и ускорение начала

(полюса) O по отношению к осям Ωζηζ , а мгновенную

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.

Кинематика

Краткий курс Теоретической Механики

28

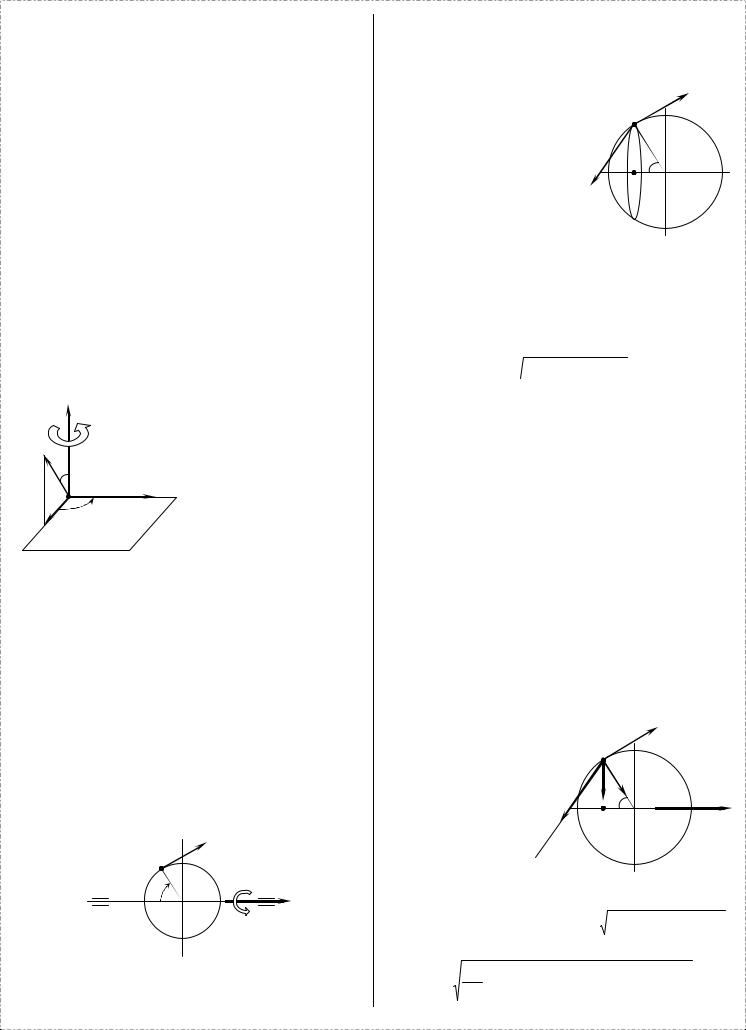
угловую скорость и угловое ускорение трехгранника Oxyz по отношению к тем же осям Ωζηζ , через ωe и εe .

Рассмотрим точку M , совершающую движение, которое вообще не зависит от движения системы Oxyz .

ζ	z		εe
			ωe	y
	M
ρ	r	O		vo
	ρo		wo
Ω				η
ξ		x
Обозначим	через ρ	и r ее абсолютный и

относительный радиус-векторы, а через ρo радиус-вектор точки O , тогда в любой момент времени

ρ = ρo + r .

(8.2)

Возьмем от обеих частей этого равенства полную производную по времени и, с учетом полученных выше формул, будем иметь:

vr

=

dρr

=

dρro

+

drr

=

a

dt

dt

dt

(8.3)

r

~r

r

r

r

r

r

dr

r

= vo

+

+ ωe × r

= vo

+ ωe

× r

+ vr .

dt

Но vo

+ ωe × r есть скорость той неизменно связанной

с системой Oxyz точки

M′, в которой в данный момент

находится точка

M , следовательно, по определению это –

переносная скорость, т. е.

ve

= vo + ωe ×r .

(8.4)

В результате из (8.3) получаем:

va

= ve + vr ,

(8.5)

т.е. мы другим путем доказали теорему о сложении скоростей.

Величину абсолютной скорости можно вычислить по

следующей формуле v2	= v2	+ v2	+ 2v v	r	cos γ , где γ –
a	e	r	e

угол между векторами скоростей ve и vr .

Возьмем теперь производные от обеих частей равенства

(8.5) с учетом (8.4):

dva

=

dve

+

dvr

=

dt

dt

dt

dvr

d

r

r

r

=

(v

+ ω

× r) +

r

=

dt

dt

o

r

e

r

r

r

r

r

dv

o

dω

e

dr

dv

=

+

× r

+ ωe ×

+

r

.

dt

dt

dt

dt

Применяя здесь формулу (8.1) к r и vr получим:

r

r

r

r

r

~r

r

r

dv

dω

e

dr

w

=

o

+

× r

+ ω

×

+ ω

× r

+

e

e

a

dt

dt

dt

(8.6)

~r

dv

r

r

+

r

+ ω

e

× v .

dt

r

Поскольку

r&

r

r&

r

и

~r

r

формулу

vo

= wo

, ωe

= εe

dr

/ dt = vr

(8.6) перепишем в виде

r

~r

r

r

r

r

r

r

r

r

dv

w

a

=

r

+ w

o

+ ε

e

×r

+ ω

e

×(ω

e

×r)

+ 2ω

e

×v

r

. (8.7)

dt

Рассмотрим слагаемые, входящие в правую часть

равенства (8.7).

~r

~2 r

r

Вектор

=

dvr

=

d r

(8.8)

wr

dt

dt2

есть по определению относительное ускорение (как локальная производная от относительной скорости по времени). В этом можно убедиться, положив в (8.7) одновременно ωe = 0 , εe = 0 и wo = 0 , т.е. считая оси

Oxyz неподвижными. Тогда полное ускорение wa точки M должно совпасть с относительным wr и мы придем к равенству (8.8).

Векторная величина

we = wo + εe ×r + ωe ×(ωe ×r)

(8.9)

есть переносное ускорение, так как, она равна ускорению той неизменно связанной с системой Oxyz точки M′, в которой в данный момент находится точка M . Иным путем это можно получить, положив в (8.7) vr = 0 и wr = 0 , т.е. считая, что точка M неизменно связана с системой Oxyz . Тогда ее полное ускорение wa совпадает с переносным we и мы получим равенство (8.9).

Векторная величина
wk = 2 ωe × vr ,	(8.10)

которая не входит ни в относительное, ни в переносное ускорения, называется поворотным или кориолисовым ускорением.

В результате получаем следующую теорему о сложении ускорений или теорему Кориолиса: абсолютное ускорение

точки при сложном движении равно геометрической сумме относительного, переносного и кориолисова ускорений

wa = wr + we + wk .

(8.11)

Если переносное движение (движение подвижной системы Oxyz ) является поступательным, то wk = 0 ,

так как ωe = 0 , и мы имеем:

wa = wr + we .

(8.12)

Следовательно, при поступательном переносном движении абсолютное ускорение точки равно геометрической сумме относительного и переносного ускорений.

Кориолисово ускорение появляется только тогда, когда подвижные оси вращаются (отсюда термин «поворотное» ускорение). Как видно из хода доказательства формулы (8.6), вектор wk является суммой двух векторов ωe × vr .

Один из них учитывает изменение вектора относительной скорости vr , при непоступательном

переносном движении, а другой – изменение переносной скорости ve при относительном перемещении точки (при

изменении вектора r в относительном движении).

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.

Кинематика

Краткий курс Теоретической Механики

29

Если система Oxyz движется поступательно, равномерно и прямолинейно, то ωe = 0 , εe = 0 , wo = 0 , и, как видно из (8.9)-(8.10): we = 0 и wk = 0 , т.е. в этом

случае относительное и абсолютное ускорения совпадают wa = wr .

Отметим, что кориолисово ускорение может обращаться в нуль в данный момент времени, когда в этот момент

r	r
времени ωe = 0 , или vr = 0 , или же ωe	|| vr .
В тех случаях, когда wk ≠ 0 , его	модуль, согласно
(8.10), вычисляется по формуле
wk = 2ωevr sin(α) ,	(8.13)

где α – угол между векторами ωe и vr , а направление wk определяется направлением произведения ωe × vr .

Направление wk можно еще найти, спроектировав вектор vr на плоскость π, перпендикулярную к ωe , и повернув эту проекцию vrπ на 90° в сторону переносного вращения (правило Жуковского).

Такой способ удобен в случае плоского движения, когда вектор vr уже лежит в плоскости, перпендикулярной к ωe .

ωe		При	решении		задач
		следует иметь в виду, что
vr α		относительная скорость vr
		и относительное		ускорение
	wk	wr вычисляются обычными
		методами кинематики точки;
90o		при этом подвижная система
		отсчета	Oxyz	рассматри-
vr π	π	вается	как	основная
		(неподвижная).
Переносная	скорость ve	и переносное ускорение we
вычисляются как скорость		и ускорение той		точки	M′
подвижной системы отсчета		Oxyz ,	с которой в данный

момент совпадает движущаяся точка С. Поскольку подвижная система движется как абсолютно твердое тело, то вычисление ve и we производится по формулам

кинематики твердого тела. Наконец, кориолисово ускорение wk вычисляется по формулам (8.10) или (8.13).

Теоретический пример По ободу диска радиуса R , вращающегося вокруг своего диаметра с постоянной угловой скоростью ω, движется с постоянной по модулю скоростью v точка M . Найти абсолютную скорость и абсолютное ускорение точки M как функцию угла ϕ , составленного радиус-вектором

точки M с осью вращения диска AB .

	M		v
A	ϕ		B
			ω
		O

MO = R

Решение

Движение точки M по ободу диска будет ее относительным движением (vr = v) .

Вращательное движение самого диска вокруг оси AB будет для точки M переносным движением ωe = ω.

При таком переносном движении в данный момент времени точка M будет вместе с соответствующей точкой

диска совершать	движение по		vr
окружности	радиуса	M
MM′ = R sin ϕ	с центром
M′ на оси вращения AB .			ϕ
Величина	переносной
скорости ve для точки M		M′	O
может быть найдена по формуле		v
Эйлера, т.е. ve = MM′ ωe или		e
ve = ωR sin ϕ.

Поскольку вектор относительной скорости v точки M лежит в плоскости диска, а переносная скорость ve

перпендикулярна этой плоскости, т.е. ve v , и, поскольку

va = vr + ve , то va2 = vr2 + ve2 = v2 + ω2R2 sin2 ϕ .

Окончательно имеем

vM = v2 + ω2R2 sin2 ϕ .

		Поскольку относительная скорость vr точки M не
	изменяется		по	величине,		то	относительное		ускорение
	r	r	r	будет представлено				только	нормальной
	w	= wτ + wn
	r	r	r	r	r	r
	составляющей						= 0) ,	по отношению к
				w	= wn ,	(wτ
				r	r	r

траектории относительного движения (окружность с центром в точке O ). Поэтому wr = wrn = v2R .

Поскольку ω = const , то ω& = ε = 0 , а, следовательно, переносное ускорение wre = wreвр + wreос точки M будет

иметь только осестремительную составляющую wre = wreос ,

(wreвр = 0) , weос = MM′ ω2 = ω2 R sin ϕ.

Ускорение Кориолиса wk = 2 ωe × vr для точки M

будет ортогонально плоскости диска и направлено в соответствии с правилом векторного произведения. На

рисунке это ускорение коллинеарное с вектором										ve . По
величине оно равно w = 2ω						v sin(90o − ϕ) = 2ωv cos ϕ .
				k	e		r
	Таким образом
r		r	r	r					vr
w	M	= wос + wn		+ w .
		e	r	k			M			y
	Спроектируем			это
								r
векторное равенство на								wn
							wос	r		ω
оси Mxyz :								ϕ
							r
		= wос	+ wn sin ϕ,		wk		e
w	Mx							M′	O
		e	r
wMy = wrn cos ϕ,					z
wMz = wk .							x
	После этого абсолютное					ускорение точки M может
быть вычислено по формуле:						wM =		wMx2 + wMy2		+ wMz2 ,
или окончательно:
	wM =		v4	+ ω4R2 sin2			ϕ + 2ω2v2 (1 + cos2 ϕ) .
			R2

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.