termex / Theoretical_Mechanics_part_02_03

Статика

Краткий курс Теоретической Механики

36

§ 5. Момент силы.

5.1. Момент силы относительно центра. r

Пусть задана сила F , приложенная в точке A какоголибо твердого тела, и некоторый центр O .

Тогда моментом силы F относительно центра O

r

будет называться вектор momo (F) , приложенный к центру O и равный векторному произведению радиус-вектора r

точки приложения A силы r

центра O на вектор силы F :

momo (F)

rr× F

C

O

F относительно выбранного

= rr × F .

(5.1)

B

F

h A

r

r

Модуль (величина) вектора момента momo (F) равен площади параллелограмма OABC , построенного на векторах r и F . Если ввести расстояние h от центра O

до линии действия силы F , называемое плечом силы F , то получим

momo (F) = | rr × F | = F r sin(α) = F h . (5.2)

Размерность величины момента силы относительно центра есть [Н м] .

Очевидно, что когда линия действия силы F

проходит через центр O, ее момент относительно этого центра равен нулю (так как плечо силы h равно нулю).

Проведя через центр O какую-нибудь систему прямоугольных осей Oxyz , мы можем представить момент

силы F относительно центра O в виде

			r		r	r
r	r	r	i		j	k
momo (F) = r		× F =	x		y	z	=
			Fx	rFy		Fz	(5.3)
r							r
= (yFz − zFy ) i	+ (zFx − xFz ) j				+ (xFy − yFx ) k

Формула (5.3) позволяет вычислить момент силы относительно начала координат, если известны проекции

(Fx, Fy, Fz ) силы F на эти оси координат и координаты точки A(x, y, z) приложения этой силы.

Когда все силы лежат в плоскости, то векторы, изображающие моменты этих сил относительно какого-либо центра, лежащего в той же плоскости, будут перпендикулярны к этой плоскости. Поэтому в данном случае моменты сил будут различаться между собой только числовой величиной и знаком и эти моменты можно рассматривать как скалярные величины.

Придерживаясь правой системы ориентировки, принято считать момент положительным, если сила стремится «вращать» тело около центра O против хода часовой стрелки, и отрицательным – если «вращает» около центра O по ходу часовой стрелки.

При этом считается, что плоскость сил совмещена с плоскостью рисунка. Тогда в случае плоской системы сил

momo (F) = ±F h .

(5.4)

5.2. Момент системы сил относительно центра.

Если мы имеем систему сил F1, F2, F3,KFn , приложенных к АТТ, то вектор

r	n	r	n	r	r	(5.5)
Mo	= ∑momo (Fi ) = ∑			(ri	× Fi ) ,
	i=1		i=1

равный сумме моментов этих сил относительно центра O ,

называется главным моментом системы этих сил относительно центра О.

Μo	F1	F2	Μo	F1		F2
	r1	r2	Fn			Fn
		rn	O	rA	A
O

Если все силы приложены к одной точке A , то

r	n	r	r	r	n	r	(5.6)
Mo	= ∑	(rA	× Fi ) = rA		× ∑Fi .
	i=1				i=1

Следовательно, момент суммы сил, приложенных к

одной точке, относительно какого-либо центра равен сумме моментов этих сил относительно того же центра (теорема Вариньона).

5.3. Момент силы относительно оси.

Моментом силы относительно оси называется проекция момента силы, взятого относительно любой точки оси, на эту ось, например

momx (F) = (rr × F)x .

(12.7)

Докажем, что проекция момента силы F , взятого относительно некоторой точки O оси Ox , на эту ось не зависит от положения точки O на этой оси. Для этого представим равенство (12.7) в виде

momx (F) = (rr × F)x = (rr × F) i = (i × rr) F .

	x	F
		d
rr× F
		A

i r

O

i

O′

Выражение (i × rr) , как это видно на рисунке, есть величина постоянная, численно равная удвоенной площади треугольника с основанием i и высотой d = r sin(i, rr) . Как основание, так и высота – величины постоянные, сила

Fтак же остается постоянной.

Следовательно, величина momx (F) не зависит от

положения точки O на оси.

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.

Статика

Краткий курс Теоретической Механики

37

Моменту силы относительно оси можно дать другое

определение, равносильное предыдущему: момент силы F

относительно какой-либо оси Ox есть момент

проекции силы F на плоскость, перпендикулярную к оси Ox , взятый относительно точки O1 пересечения оси Ox с этой плоскостью.

rr× F		x	F
			r
	O
		h	FA
	O1
		rA	A

При этом момент проекции FA относительно точки O1 рассматривается как скалярная величина, имеющая знак плюс, если поворот, совершаемый силой FA , виден с

положительного конца оси Ox против хода часовой стрелки, и знак минус – если по ходу часовой стрелки.

Таким образом

momx	(F) = momO (FA ) = ±FA h1 .	(5.8)
	1

Из предыдущего следует, что если линия действия силы F пересекает ось Ox или ей параллельна, то момент силы F относительно этой оси равен нулю.

Моменты силы F относительно осей какой-либо прямоугольной системы координат Oxyz можно, пользуясь

равенством (5.3), представить в виде формул одновременно

							r	r	r
определяющих проекции вектора momo (F) = r									× F на оси
координат:		r		r
mom			r			= yF	− zF ,
		(F) = (r		× F)
	x	r	r	r	x	z	y	,	(5.9)
mom		(F) = (r		× F)		= zF	− xF
	y	r	r	r	y	x	z
momz (F) = (r				× F)z = xFy − yFx,

§ 6. Теория пар сил.

6.1. Момент пары.

Парой сил называется система двух равных по величине и не лежащих на одной прямой антипараллельных сил, действующих на абсолютно твердое тело.

	Расстояние	d	между	r r
	линиями действия		сил пары
				mom(F, F′)
	называется плечом пары.
	Плоскость,	в	которой	B
	действуют	силы	пары,

называется	плоскостью	F′	F
действия пары.			A
Совокупность	нескольких

пар сил, действующих на АТТ, называется системой пар.

Ранее было показано, что пара сил не имеет равнодействующей и, действуя на твердое тело, стремится сообщить ему некоторое вращение. Вращательный эффект пары сил характеризует вектор-момент пары сил.

Момент пары сил есть вектор

r	r	′	r	′	=	r	(6.1)
mom(F, F ) = AB × F						BA × F ,
перпендикулярный		к	плоскости			действия	пары,

направленный по правилу правого винта и численно равный

произведению одной из сил пары на ее плечо, т.е. r

mom(F, F′) = F d .

Если		пары		расположены			в
одной	плоскости,			то их		векторы-			d	F
моменты		будут			направлены
перпендикулярно к этой плоскости								F′	« + »
в ту	или		иную		сторону,		в
зависимости			от		направления
вращения пары.
Поэтому			в	данном		случае
моменты		пар	будут		отличаться			F′	d
между	собой		только			числовой				F
величиной		и	знаком,		т.е. могут				« – »
рассматриваться				как	величины
скалярные.
Условимся,			придерживаясь				правой системы,			считать

момент пары, вращающей против хода часовой стрелки, положительным, а по ходу стрелки часов – отрицательным. Тогда для плоской системы пар

′	(6.2)
mom(F, F ) = ±F d .

Приводимые ниже теоремы об эквивалентности пар сил показывают, что вектор-момент пары сил может быть приложен в любой точке твердого тела, т.е. является свободным вектором.

Теорема 1. Момент пары сил есть сумма моментов

сил пары относительно любого центра.

Возьмем

произвольный

F

центр O и проведем из него

радиусы-векторы rA и rB в

B

A

точки A и B , где приложены

силы пары (F,

′

F ) .

F′

Тогда

r

r

и,

r

rA

BA = r

A

− r

B

B

учитывая

что

− F = F′,

O

получим

r

r

r

r

=

=

r

BA × F

(r

− r

) × F

r

(6.3)

r

r

×

rA

r B

r

r

= r

A

× F

− r

F = r

A

× F + r

× F′,

B

B

что и требовалось доказать.

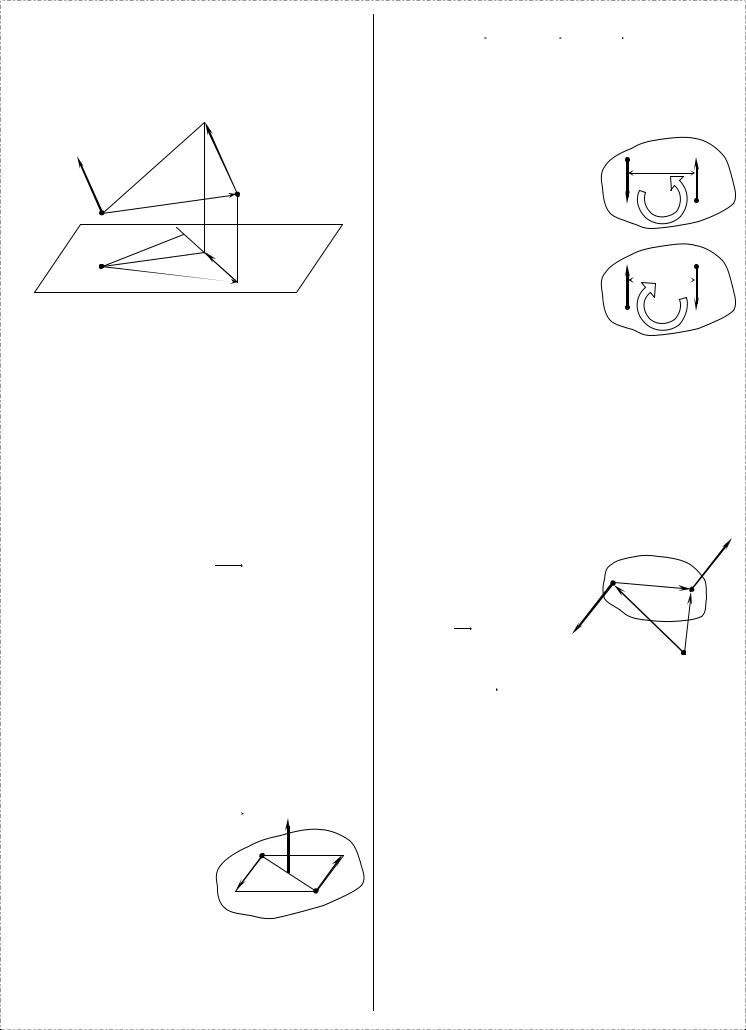
Теорема 2. Действие пары сил на АТТ не изменится,

если переместить пару в другое положение в плоскости ее действия.

Пусть мы имеем пару (F1, F2 ) , причем силы пары

приложены к концам плеча пары A и B . Переместим плечо пары AB в некоторое новое положение, например

A1B1 . Приложим в точках A1 и B1 по две силы F3 , F4 и

F5 , F6 , равные силам пары (F1, F2 ) и направленные в противоположные стороны перпендикулярно A1B1 . Тогда

(F1, F2 ) ~ (F1, F2, F3, F4, F5, F6 ) , т.к. (F3, F4, F5, F6 ) ~ 0 .

От пересечения линий действия сил данной пары (F1, F2 ) с линиями действия сил, приложенных к точкам A1 и B1 , получим ромб, поскольку AB = A1B1 .

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.

Статика

Краткий курс Теоретической Механики

38

Перенесем силы F и F

r

Теорема 4. Действие пары сил на АТТ не изменится,

A

F2

1

4

B

если любым способом видоизменить силы и плечо пары,

в

точку

K

пересечения

r

сохраняя

постоянным

их

произведение, т.е.

момент

линий их действия.

F1

r

пары.

Эти силы, как равные по

A1

K

F

C

модулю,

будут

иметь

4

r

r

Пусть мы имеем пару

(P1, P2 ) .

Разложим силу

P2

на

r

равнодействующую, направ-

F

F6

F4

две силы

Q и

(P2 − Q) ,

приложенные в точках

C и

A .

1

r

r

r

ленную по биссектрисе угла

F2

F5

F3

Силы

P

и

(P − Q)

имеют равнодействующую

Q′,

CKD , т.е. по диагонали

D

r

L

B

F

1

2

Q′ = P − (P − Q) = Q .

ромба KCLD .

5

1

модуль

которой

равен

В

Силы F

и F

перенесем в противоположную вершину

1r

′ r

2

2

5

результате мы получим новую пару (Q , Q) , плечо которой

L

ромба.

Эти

силы

также дадут

равнодействующую,

равно

AC , причем для этой пары силы

Q и плечо

AC

численно равную предыдущей, и направленную по той же

удовлетворяют соотношению

диагонали, но в противоположную сторону. Следовательно,

Q AB = P2 AC

или

Q AC = P2 AB .

(6.4)

равнодействующие сил F1 , F4

и сил F2 , F5 уравновесятся,

Но произведение Q

′

т.е. система (F1, F2, F4, F5 ) ~ 0 .

AC есть момент пары сил (Q , Q) ,

а P2

AB есть момент пары сил (P1, P2 ) .

Таким образом, система сил (F1, F2 )

эквивалентна

Таким

образом,

P2 − Q

P2

системе

(F , F ) ,

другими

словами

пара

сил

(F , F )

данную пару

сил

всегда

3

6

1

2

можно привести к данной

Q

эквивалентна паре сил (F3, F6 ) .

силе или к данному плечу

A

Теорема 3. Действие пары сил на АТТ не изменится,

B

при условии

сохранения

Q′

C

если ее перенести в плоскость, параллельную плоскости

величины

ее

момента,

P

действия пары.

теорема доказана.

1

Пусть мы имеем пару сил (F1, F2 )

с

плечом

AB .

Из доказанных выше теорем следует, что: 1) вектор-

Перенесем

плечо

AB

параллельно

самому

себе

в

момент пары сил может быть переносим в любую точку

положение A1B1 ,

и

к точкам

A1

и

B1

приложим

пространства и он есть вектор свободный, и 2) пары сил,

направленные в противоположные стороны силы F ,

F

и

имеющие равные векторы-моменты, эквивалентны,

F5 , F6 , равные

по

величине

силам

пары

3

4

и

поскольку одна из этих пар может быть преобразована в

(F1, F2 )

другую.

параллельные им.

Теорема 5. Система пар сил, действующих на АТТ,

r

эквивалентна

одной

паре,

момент

которой

равен

r

векторной сумме моментов этих пар.

F4

2F

F6

пар

сил

A1

r

B1

Пусть

на

АТТ

действует

система

(Fi, Fi′),

r

i = 1, n ,

произвольно

ориентированных

в

F3

r

F

A

C

2

F5

пространстве.

B

r

Заменим каждую пару сил (Fi, Fi′)

эквивалентным ей

2F′

F1

r

r

вектором-моментом momi (Fi, Fi′) .

Тогда система сил (F1, F2 ) ~ (F1, F2, F3, F4, F5, F6 ) .

Поскольку вектор-момент есть свободный вектор, то его

Соединив концы плеч, получим параллелограмм.

можно прикладывать в произвольной точке АТТ. Выберем

Сложив

силы

F

и

F ,

получим

равнодействующую,

в качестве такого центра некоторую точку O данного тела.

2

4

Тогда,

осуществляя указанный перенос всех векторов-

равную 2F , которая будет приложена в середине

r

r

диагонали параллелограмма и направлена вверх. Сложим

моментов momi (Fi, Fi′) в

этот центр, получим систему

силы

F

и

F , получим их равнодействующую,

равную

векторов-моментов, приложенных в одной точке O .

1

5

Построенная таким образом система векторов-моментов,

− 2F

и направленную вниз.

Точка ее приложения будет

имеет

равнодействующий

вектор

Mom ,

равный

также в середине диагонали параллелограмма. Таким

r

r

образом, обе равнодействующие имеют общую точку

геометрической сумме ∑momi (Fi, Fi′)

векторов-моментов

приложения, равны между собой и направлены в

исходных пар сил.

противоположные

стороны,

следовательно,

они

взаимно

Найденный

результирующий

вектор-момент

Mom

уравновешиваются.

можно представить в виде пары сил

′

, лежащей в

Отсюда

вытекает,

что

система

(F , F , F , F ) ~ 0 .

(F, F )

1

5

2

4

плоскости

ему

перпендикулярной

и

такой,

что

Поэтому

(F1, F2, F3, F4, F5, F6 ) ~ (F3, F6 )

и

пара

сил

r r′

mom(F, F ) = Mom .

r

r

r

r

(F3, F6 ) эквивалентна паре сил (F1, F2 ) .

Откуда имеем

mom(F, F′) = ∑momi (Fi, Fi′) ,

что и

требовалось доказать.

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.