termex / Theoretical_Mechanics_part_01_06

Кинематика

Краткий курс Теоретической Механики

19

§ 6. Сложные движения твердого тела

6.1. Общая постановка задачи.

Будем рассматривать твердое тело, движущееся относительно системы отсчета Oxyz , которая в свою

очередь перемещается некоторым образом по отношению к неподвижной системе Oξηζ .

Пусть v1	есть скорость точки		M тела в его движении
относительно	подвижных	осей	Oxyz	(относительная
скорость), а v2 – скорость той			неизменно связанной		с
подвижной системой Oxyz точки пространства M′,					с
которой в данный момент		времени совпадает точка M
(переносная скорость).
Если относительное и переносное движения тела
известны, то абсолютная скорость точки				M будет равна
геометрической сумме
	vM = v1 + v2 .			(6.1)

Рассмотрим следующую задачу: пусть в данный момент времени известны относительное и переносное движения АТТ, необходимо установить вид результирующего (сложного) движения тела, которому соответствует распределение абсолютных скоростей точек тела в этот момент времени.

Поскольку задача ставится для данного момента времени, можно говорить о решении проблемы сложения n мгновенных поступательных и вращательных движений абсолютно твердого тела.

Из равенства (6.1) вытекает, что слагаемые движения кинематически коммутативны в том смысле, что мгновенное распределение скоростей результирующего движения не изменится, если относительное и переносное движения поменять ролями.

6.2. Сложение поступательных скоростей.

Пусть все составные движения АТТ являются поступательными, тогда, в отличие от всех последующих случаев, теорема о сложении скоростей формулируется и доказывается одинаково как для мгновенных, так и для конечных перемещений.

Пусть АТТ движется поступательно со скоростью v1 относительно системы Oxyz , которая в свою очередь движется поступательно со скоростью v2 относительно неподвижной системы Oξηζ .

Тогда абсолютная скорость каждой точки тела есть сумма относительной скорости, которая для всех точек тела равна v1 , и переносной скорости, которая в этом случае для

любой точки АТТ равна v2 . Поэтому абсолютные скорости

всех точек тела выражаются одним и тем же вектором
v = v1 + v2 ,	(6.2)

а результирующее движение АТТ будет поступательным. Если тело участвует одновременно в n поступательных

движениях со скоростями v1, v2,K, vn , то результирующее

его движение будет также поступательным с абсолютной скоростью

v = v1 + v2 + K + vn .

6.3. Сложение мгновенных угловых скоростей.

Пусть АТТ совершает мгновенное вращение с угловой скоростью ω1 относительно системы Oxyz , которая, в

свою очередь, совершает также мгновенное вращение с угловой скоростью ω2 по отношению к неподвижной

системе Oξηζ.

Рассмотрим частный случай, когда мгновенные угловые скорости пересекаются в одной точке О.

Построим на векторах ω1 и ω2 параллелограмм.

Тогда скорость точки			A (точка конца диагонали этого
параллелограмма) будет равна
r	r	× OA		r	× OA = 0 .
vA	= ω1			+ ω2
	v				A
			r		vM
	ω
	1		Ω

M

r

O ωv2

Модули обоих слагаемых равны, т.к. они равны удвоенным площадям равных треугольников, составляющих параллелограмм.

По направлениям же эти слагаемые противоположны, а поэтому скорость точки A равна нулю. Следовательно прямая, проходящая через точки O и A является мгновенной осью вращения результирующего движения, которое также является мгновенным вращением с угловой скоростью

			r	r		(6.3)
			Ω =ω1	+ω2 .
Тогда	скорость		произвольной точки		M данного тела
будет равна				r
	r	r	r			(6.4)
	vM = ω1		× OM + ω2 × OM = Ω × OM .
Если	АТТ одновременно			участвует	в n мгновенных
вращениях с угловыми скоростями ω1, ω2,K, ωn						вокруг

осей, пересекающихся в одной точке O , то результирующее движение будет также мгновенным вращением вокруг оси, проходящей через точку O , с угловой скоростью

r	r	r	(6.5)
Ω = ω1	+ ω2	+K+ ωn .

Рассмотрим теперь случай, когда мгновенные угловые скорости параллельны и направлены в одну сторону.

Очевидно, что это будет случай плоскопараллельного движения АТТ в плоскости, перпендикулярной к мгновенным угловым скоростям.

Пусть плоскость движения АТТ пересекает плоскость осей ω1 и ω2 по прямой AB . Скорости, которые получает

от мгновенных вращений с угловыми скоростями ω1 и ω2

некоторая точка M , лежащая на отрезке AB , будут противоположны по направлению, а по величине эти скорости будут равны ω1 AM и ω2 BM .

Следовательно, одна из точек отрезка AB , а именно C , для которой будет справедливо равенство

ω	AC = ω	2	BC или	AC	= ω2	(6.6)
1				BC	ω1

имеет скорость, равную нулю, т.е. vC = 0 .

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.

Кинематика

Краткий курс Теоретической Механики

20

Такую же скорость будут иметь все точки, лежащие на прямой, проходящей через точку C и параллельной мгновенным осям вращений.

Поэтому эта прямая будет мгновенной осью вращения для результирующего движения

r

Ω

ωv1 ωv2

M

A C B

Для определения мгновенной угловой скорости Ω результирующего движения рассмотрим скорость точки B .

Имеем vB = ω1 AB + ω2 0 = ω1 AB ,

но с другой стороны

vB = Ω CB , откуда								Ω CB = ω1 AB .
Используя (6.6), окончательно имеем
Ω = ω		AB		= ω		AC + CB			=
1		CB			1	CB					(6.7)
	AC							ω
= ω					+ 1	= ω		2 +		1	= ω + ω .
1	CB					1		ω1			2 1

Итак, результирующее движение есть мгновенное вращение с угловой скоростью Ω = ω1 + ω2 . Мгновенная

угловая скорость (ось вращения) расположена в плоскости мгновенных угловых скоростей ω1 и ω2 слагаемых

движений, параллельна им, направлена в ту же сторону и делит расстояние между ними внутренним образом на части, обратно пропорциональные величинам ω1 и ω2 .

Пусть теперь мгновенные угловые скорости антипараллельны, т.е. векторы ω1 и ω2 параллельны, но

направлены в противоположные стороны.

Построим плоскость движения АТТ, перпендикулярную к обеим мгновенным осям, и прямую AB , по которой плоскость движения пересекается с плоскостью осей.

ωv1

r

Ω

M B

C A

ωv2

Пусть ω1 ≠ ω2 и ω1 > ω2 . Для любой точки M , лежащей на продолжении отрезка AB за большей мгновенной угловой скоростью ω1 , скорости,

происходящие от мгновенных вращений с угловыми скоростями ω1 и ω2 противоположны по направлению, а

по величине равны ω1 AM и ω2 BM .

Тогда одна из этих точек, а именно C , для которой

ω	CA = ω CB или	CA	= ω2	(6.8)
1	2	CB	ω1

имеет скорость, равную нулю, т.е. vrC = 0 .

Следовательно, прямая, параллельная ω1 и ω2 , и

проходящая через C , есть мгновенная ось вращения для результирующего движения.

Для точки B имеем

vB = ω1 AB = Ω CB ,

где Ω – мгновенная результирующая угловая скорость. Отсюда вытекает

Ω = ω

AB

= ω

CB − CA

=

CB

1

1 CB

(6.9)

CA

ω

= ω

1 −

= ω

1

−

2

= ω − ω .

1

CB

1

ω1

1

2

Таким образом,

когда

ω1 ≠ ω2

и

ω1 > ω2 ,

результирующее движение есть мгновенное вращение с угловой скоростью, численно равной Ω = ω1 − ω2 .

Вектор мгновенной угловой скорости	Ω расположен в
плоскости угловых скоростей ω1 и	ω2	слагаемых

движений, параллелен им, направлен в сторону большей скорости ω1 и делит расстояние между векторами ω1 и ω2

внешним образом на части, обратно пропорциональные модулям ω1 и ω2 .

6.4. Пара вращений.

Совокупность двух мгновенных вращений вокруг параллельных осей с одинаковыми по модулю и противоположными по направлению угловыми скоростями образует пару мгновенных вращений или, как говорят для краткости, пару вращений.

Угловые скорости ω1 и ω2 этих вращений, удовлетворяющие соотношениям

ω1 = −ω2 и		ω1 = ω2 = ω,		(6.10)
составляют пару мгновенных угловых скоростей.
			ω1
	d
		P
			M
Q
ω2		r	r
		v	= ω1 × PQ

Формулы (6.9) и (6.8) показывают, что в случае антипараллельных угловых скоростей в пределе при ω2 → ω1 результирующая угловая скорость Ω стремится

к нулю, а мгновенная ось результирующего движения уходит вместе с точкой C на бесконечность, так как в пределе AC → BC .

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.

v = ω d .

Кинематика

Краткий курс Теоретической Механики

21

Отсюда можно заключить, что результирующее движение дает мгновенное поступательное движение или, иначе, что пара мгновенных угловых скоростей эквивалентна поступательной скорости.

Действительно, обозначая через P и Q какие-нибудь

две точки, взятые на мгновенных осях вращения, будем для любой точки M тела иметь:

r		r		r	r	r
v	M	= ω × PM		+ ω × QM = ω × PM − ω × QM =
		1	r	2	1 r	1
			= ω1	× (PM − QM) = ω1		× PQ.

Итак, скорости всех точек тела в данный момент времени равны друг другу, следовательно, пара мгновенных угловых скоростей (ω1, ω2 ) действительно

эквивалентна поступательной скорости

		r	r	× PQ .	(6.11)
		vM	= ω1
При этом скорость v результирующего поступательного
движения перпендикулярна к плоскости пары					(ω1, ω2 ) и
направлена так, что наблюдатель, смотрящий с конца						v ,
видит векторы		пары	(ω1, ω2 ) указывающими			на
«вращение» против хода стрелки часов.
Расстояние	d	между		мгновенными	угловыми

скоростями (ω1, ω2 ) называется плечом пары.

Модуль v численно равен площади параллелограмма, построенного на векторах (ω1, ω2 ) , т. е.

(6.12)

Вектор v , определяемый равенством (6.11), называется моментом пары; а поскольку он может быть приложен в любой точке тела, то это свободный вектор.

Следовательно, пара мгновенных угловых скоростей

эквивалентна мгновенной поступательной скорости, равной моменту этой пары.

Наоборот, всякая поступательная скорость v может быть представлена в виде пары мгновенных угловых скоростей, плоскость которой перпендикулярна к v , а плечо d и модули мгновенных угловых скоростей ω1 = ω2 = ω удовлетворяют равенству (6.12).

Если тело имеет вrданный момент мгновенное вращение с угловой скоростью ω вокруг оси, проходящей через точку

A , то состояние		движения	не изменится,			если в любой
точке B приложить два вектора ω				′		′
					= ω и −ω = −ω.
	ω′				ω
					A
	B				v
		−ω′
Но векторы	r	r				эквивалентную
	ω	и −ω′ образуют пару,
поступательной	скорости		r r			Следовательно,
			v = ω× AB .

мгновенное вращение тела с угловой скоростью ω вокруг оси, проходящей через точку A , эквивалентно мгновенному вращению с такой же угловой скоростью

′
ω =ω вокруг параллельной оси, проходящей через любую
точку	r r
	B , и поступательной скорости v = ω× AB .

6.5. Сложение мгновенных угловой и поступательной скоростей.

Пусть теперь твердое тело совершает относительно системы Oxyz мгновенное вращение с угловой скоростью

ω, а сама эта система совершает по отношению к неподвижной O1ξηζ поступательное движение со

скоростью v (или наоборот, что в силу коммутативности мгновенных движений несущественно). Рассмотрим возможные частные случаи.

1) Поступательная скорость перпендикулярна к

мгновенной оси вращения Aa .
Заменим в этом случае мгновенную	поступательную
′	′	) , где ω	′	= ω
скорость v парой угловых скоростей (ω,−ω
		′		′	)
– заданная угловая скорость, и расположим пару (ω ,−ω

так, как показано на рисунке; при этом, согласно (6.12), плечо пары d = v / ω.

Тогда мгновенные вращения вокруг одной и той же оси Aa с угловыми скоростями ω и − ω′ взаимно уничтожатся и останется только мгновенное вращение тела вокруг мгновенной оси Bb с угловой скоростью ω′.

aω′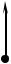b

ωB

d

A

v

−ω′

Итак, при сложении мгновенного вращательного движения АТТ с угловой скоростью ω и его же поступательного движения со скоростью v , направленной перпендикулярно к ω, результирующее движение будет мгновенным вращением с такой же (по модулю и направлению) угловой скоростью ω, но вокруг мгновенной оси, смещенной в плоскости, перпендикулярной к вектору v , на величину d = v / ω.

Частным примером такого случая сложения движений является плоскопараллельное движение АТТ или движение плоской фигуры в ее плоскости, которое слагается из поступательного движения вместе с полюсом и вращательного движения вокруг полюса, и которое эквивалентно в каждый момент времени мгновенному вращению с той же угловой скоростью вокруг мгновенного центра вращения.

2) Поступательная скорость v параллельна оси вращения ω.

В этом случае результирующее движение тела будет или перманентным, или мгновенным винтовым движением.

а) Винтовое движение (перманентное). Пусть движение тела слагается из равномерного вращения с угловой скоростью ω вокруг оси постоянного направления и равномерного прямолинейного поступательного движения со скоростью v , параллельной ω.

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.

Кинематика

Краткий курс Теоретической Механики

22

	v
	h
ω	M

Результирующее движение тела в этом случае называется перманентным винтовым или просто винтовым движением, а ось вращения – осью винта. Любая точка M тела остается во время такого движения на поверхности круглого цилиндра, описывая винтовую линию.

Если разрезать цилиндр по той образующей, на которой точка M находилась в момент t = to , и развернуть его

поверхность на плоскость, то в течение первого оборота

положение точки M на	развертке будет определяться
координатами
x1 = rωt ,	y1 = vt

где r – есть расстояние от точки M до оси винта.

Отсюда вытекает, что траектория точки M на развертке будет прямой линией, наклоненной к оси Ox под углом

α = arctg(vrω) .

	y1
	α		h
	α	M	vt
O
	r ωt		x1

Если в данный момент точка M находится на некоторой образующей, то через промежуток времени T = 2πω она вновь пересечет эту образующую,

переместившись вдоль нее на расстояние h = vT = 2πvω, которое не зависит от r , и называется шагом винта.

Величину p = vω называют параметром винта.

Отметим, что для винта имеют место следующие соотношения:

h = 2πp, tg(α) = p r = h 2πr .

Скорость точки M по модулю равна

vM = v2 + r2ω2 , а направление ее составляет угол α с плоскостью, перпендикулярной к оси винта.

Ускорение точки M направлено к оси винта (перпендикулярно к этой оси), а его модуль равен wM = rω2 .

б) Мгновенное винтовое движение. Если движение

тела слагается из мгновенного вращения с угловой r

скоростью ω и поступательного движения со скоростью v , параллельной мгновенной угловой скорости ω, то результирующее движение представляет собою мгновенное винтовое движение, а ось этого винта называется

мгновенной винтовой осью.

Как и мгновенная ось вращения, мгновенная винтовая ось меняет с течением времени свое положение в пространстве и в самом движущемся теле. Параметр

мгновенного винтового движения равен p = vω и будет вообще тоже величиною переменной.

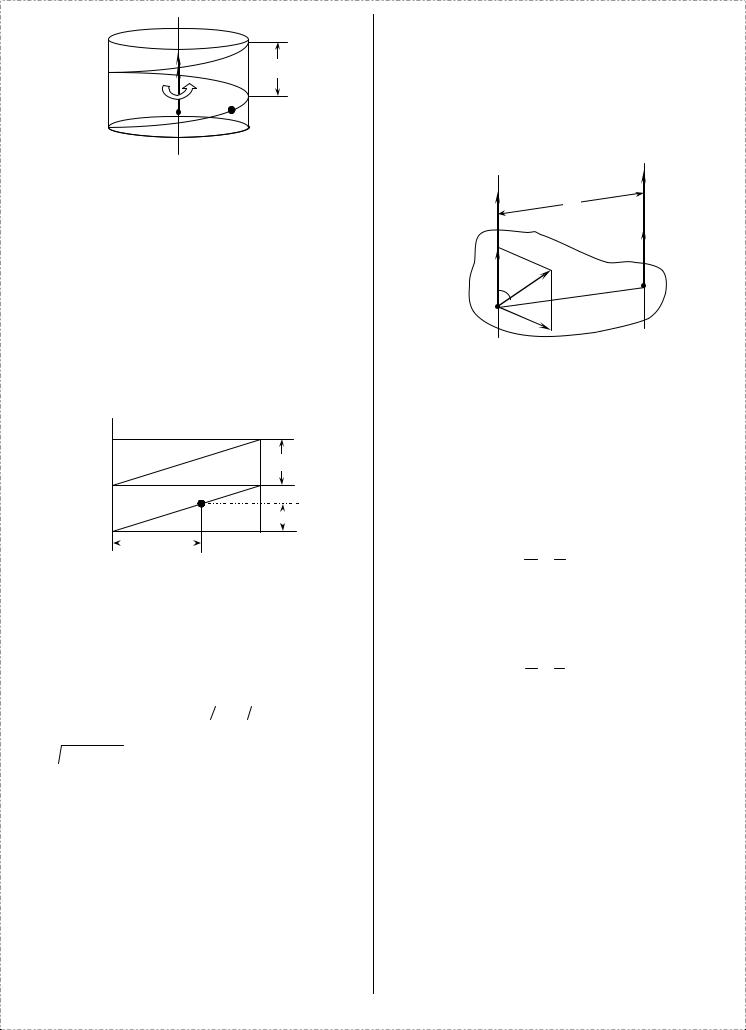
3) Поступательная скорость v образует произвольный угол α с мгновенной осью вращения Aa (с

вектором ω).

Разложим скорость v на составляющие v′ и v′′ , направленные соответственно по заданной мгновенной угловой скорости ω и по перпендикуляру к ней.

a b ω′

ωd

	v′
v′
v
α	B
A
v′′
Очевидно, что
v = v′ + v′′,
v′ = v cos(α),
v′′ = v sin(α).

Сложение мгновенной угловой скорости ω и перпендикулярной к ней поступательной скорости v′′ дает, согласно случаю 1), вращение с угловой скоростью ω′ = ω вокруг новой мгновенной оси Bb , лежащей в плоскости, перпендикулярной к вектору v′′ , при этом расстояние между осями Aa и Bb будет равно

d = vω′′ = ωv sin(α) .

В результате тело будет иметь мгновенную угловую ω′ = ω, направленную вдоль оси Bb , и параллельную ей поступательную скорость v′, которые, слагаясь, дают мгновенное винтовое движение с параметром

p = vω′ = ωv cos(α) .

Итак, результирующее движение АТТ в рассмотренном выше случае будет мгновенным винтовым движением вокруг оси Bb , параллельной вектору ω и отстоящей от оси Aa на расстоянии d .

Для заметок

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

__________________________________________________

© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ

23 марта 2007 г.