Для студентов / Лекции / (3)СТВ / (2)Кінематика руху матеріальної точки

2. Співвідношення між просторовими і часовими інтервалами. Кінематика руху матеріальної точки

В класичній фізиці, побудованій на просторово-часових уявленнях Галілея-Ньютона, відстані між двома просторовими точками і проміжки часу між двома подіями є однаковими в різних ІСВ:

. (2.1)

В СТВ ці співвідношення не виконуються, оскільки різниця координат , у згоді з перетвореннями Лоренца

, (2.2)

переходить в лінійну комбінацію . Без додаткових обмежень вона явно приводить до нерівності: . Так само встановлюється, що .

На відміну від двох інваріантів (2.1), в СТВ Айнштайна існує тільки один інваріант – інтервал руху: . Інакше кажучи, аналогом (2.1) є тільки одне співвідношення:

, (2.3)

яке залишається інваріантним відносно перетворень Лоренца.

Таким чином, в рамках СТВ Айнштайна визначення відстаней між двома просторовими точками і тривалості часових проміжків між двома подіями, а також співвідношень між ними в різних ІСВ вимагає додаткового спеціального аналізу.

а) Визначення довжини рухомого стержня

Розглянемо процес вимірювання довжини нерухомого стержня в лабораторній системі відліку (ЛСВ). До стержня прикладається масштабна лінійка. Ми дивимось, з якими позначками співпадають початок і кінець стержня, і тоді довжину стержня знаходимо як різницю знайдених координат:

. (2.4)

Якщо той же стержень рухається з постійною швидкістю прикласти до нього лінійку нерухомому спостерігачеві неможливо. Її може прикласти тільки спостерігач в системі відліку , в якій стержень стає нерухомим. В цьому випадку, якщо стержень розміщується вздовж вісі його довжина визначається так само, як і першому випадку:

. (2.5)

Тут є суттєвим те, що для нерухомого стержня значення координат точок, що відповідають положенню його початку і кінця, можуть бути виміряні в будь-які моменти часу. Очевидно, що значення довжини стержня в тих ІСВ, де він є нерухомим, повинні бути однаковими: . Величину прийнято називати власною довжиною стержня.

Але ситуація різко змінюється, коли ми перейдемо до визначення довжини рухомого стержня в ЛСВ. Оскільки масштабну лінійку в ЛСВ прикласти до стержня неможливо, потрібно дати її означення, яке б точно відповідало визначенню довжин рухомих об’єктів нашими органами зору. Неважко зрозуміти, що наш зір сприймає рухомий об’єкт в певний момент часу так само, як і фотоапарат. Це і підказує процедуру вимірювання довжини рухомого об’єкту: 1) в довільний момент часу треба зробити миттєву фотографію об’єкта разом з масштабною лінійкою, яка рухається разом з ним. Фотографія зафіксує значення координат початку і кінця стержня в фіксований момент часу; і 2) перейти від отриманих значень координат точки в рухомій ІСВ до відповідних координат точки в лабораторній ІСВ.

Спочатку розглянемо ситуацію, коли ІСВ і рухаються одна відносно другої вздовж осей і . Нехай координати кінця і початку стержня, розташованого вздовж вісі , приймають значення і . У згоді з описаною процедурою вимірювання, довжина стержня в лабораторній ІСВ визначається за формулою:

. (2.6)

Тепер встановимо зв'язок між просторовими координатами точки в рухомій і лабораторній ІСВ. З перетворень Лоренца:

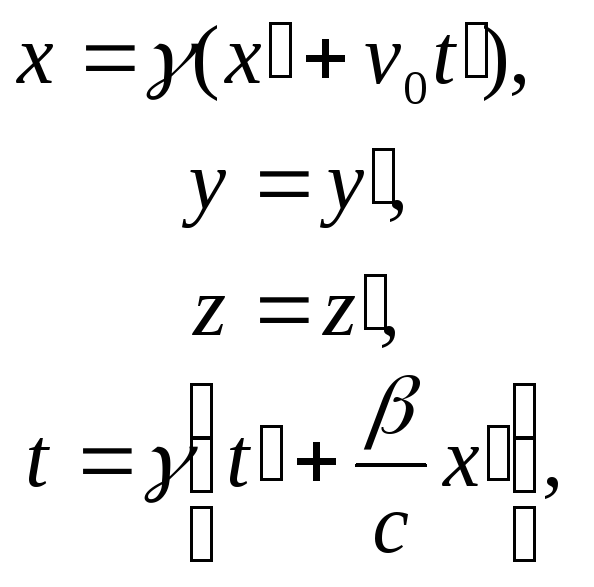
, (2.7)

випливає, що координатам і відповідають наступні значення штрихованих координат і часу:

. (2.8)

Оскільки і визначаються в один і той же момент часу за годинником ЛІСВ, то відповідні значення координат і є пов’язаними співвідношенням:

. (2.9)

Комбінуючи (2.6), (2.8) і (2.9), знаходимо:

. (2.10)

Таким чином, довжина рухомого стержня, виміряна спостерігачем в ЛІСВ за описаною вище процедурою, визначається за формулою:

. (2.11)

Бачимо, що довжина рухомого стержня виявляється коротшою за його власну довжину за універсальною законом, який не залежить від технічних деталей процесу вимірювання. Скорочення стержня відбувається не під дією зовнішніх сил, а внаслідок опосередкування електромагнітним полем, яке встановлює зв'язок між рухомим стержнем і спостерігачем.

Якщо стержень розташовується в площині його довжина в ІСВ і не змінюється:

. (2.12)

Це встановлюється точнісінько у такий самий спосіб, який використано при розташуванні стержня вздовж осей і .

В найбільш загальному випадку, коли стержень є зорієнтованим довільним чином в ІСВ , його довжина в ЛІСВ визначається співвідношенням:

.

Позначаючи: і , остаточно знаходимо наступний закон перетворення довжини стержня:

. (2.13)

б) Співвідношення між часовими інтервалами

Для визначеності, давайте розглянемо коливання гойдалки, яке може слугувати прикладом найпростішого періодичного процесу, з точки зору спостерігачів в різних ІСВ. Період коливань гойдалки з точки зору спостерігача, відносно якого точка підвісу гойдалки є нерухомою, визначається різницею:

, (2.14)

де моменти повернення підвішеної матеріальної точки гойдалки у деяку фіксовану точку простору в ІСВ . Згідно (2.7), цим моментам часу відповідають наступні моменти часу в ЛСВ:

і . (2.15)

За означенням, період коливань гойдалки в ЛСВ природно визначати співвідношенням:

.

Звідси і (2.14) випливає, що дорівнює:

. (2.16)

Період коливань гойдалки в ІСВ , де її точка підвісу є нерухомою, прийнято називати власним періодом коливань і позначати: . У згоді з цим формулі (2.16) можна надати вигляд:

. (2.17)

Таким чином, в ЛСВ спостерігається подовження власного періоду коливань, або, інакше, уповільнення часу.

Зазначимо, що цей висновок не залежить від просторової орієнтації площини гойдань гойдалки, тобто має загальний характер.

в ) Закон додавання швидкостей у СТВ

За означенням, тривимірні швидкості матеріальної точки в ІСВ і визначаються співвідношеннями:

і

відповідно. Визначимо тепер диференціали просторових координат точки і часу в ІСВ через відповідні диференціали в ІСВ . Із перетворень Лоренца випливає:

.

Підставляючи ці вирази у відповідні похідні, знаходимо наступний вигляд релятивістського закону додавання швидкостей:

(2.18)

В граничному випадку , тобто, коли швидкість розповсюдження електромагнітних сигналів прямує до нескінченості, зв'язок між компонентами швидкості в ІСВ і , як і повинно бути, має той самий вигляд, що і в класичній механіці:

.

Переконаємось, що 1) максимальні значення компонентів швидкості точки завжди залишаються меншими від швидкості світла і 2) величина швидкості точки теж залишається меншою від . Дійсно, значення похідної 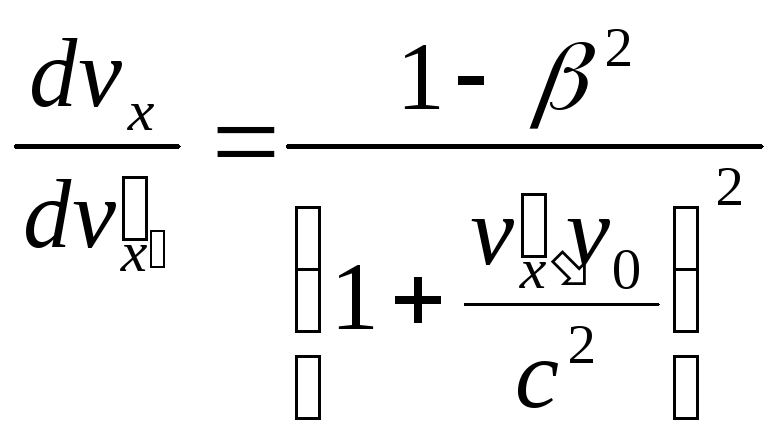як функції від залишаться позитивними при всіх значеннях . Звідси випливає, що як функції від постійно зростає і приймає максимальне значення при . Очевидно, що . Тобто, завжди .

г) Закон додавання прискорень

Для побудови відповіді на поставлене в заголовку цього підрозділу запитання, будемо виходити з означень тривимірного прискорення матеріальної точки в ІСВ і :

і .

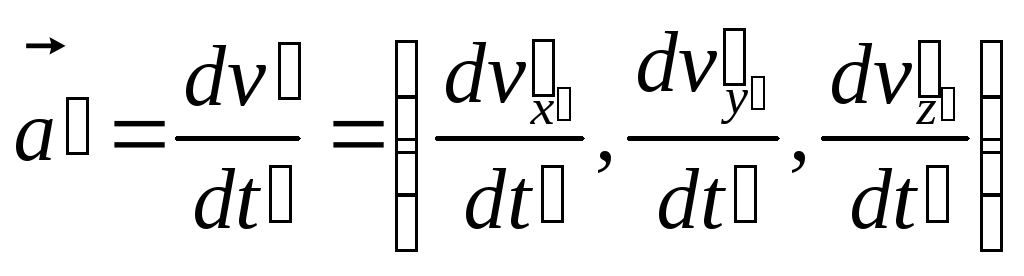Для знаходження компонентів прискорення визначимо тепер диференціали 1) компонентів швидкості згідно формул () і 2) поділимо їх на диференціал часу: . На першому кроці ми отримуємо:

.

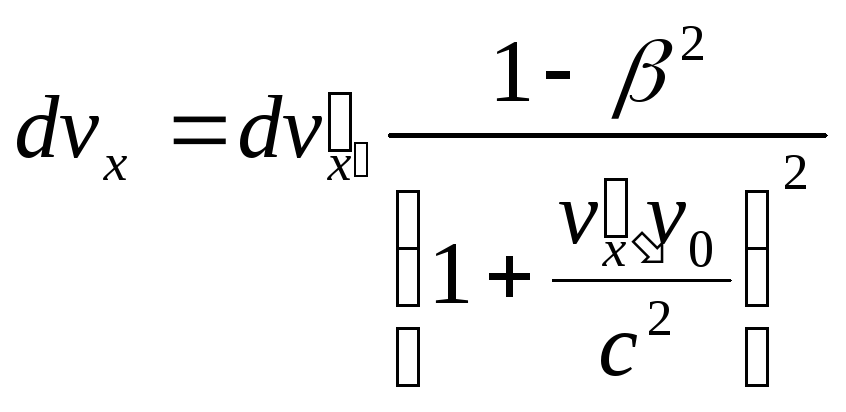Ділення диференціалу швидкості на диференціал часу приводить до результату:

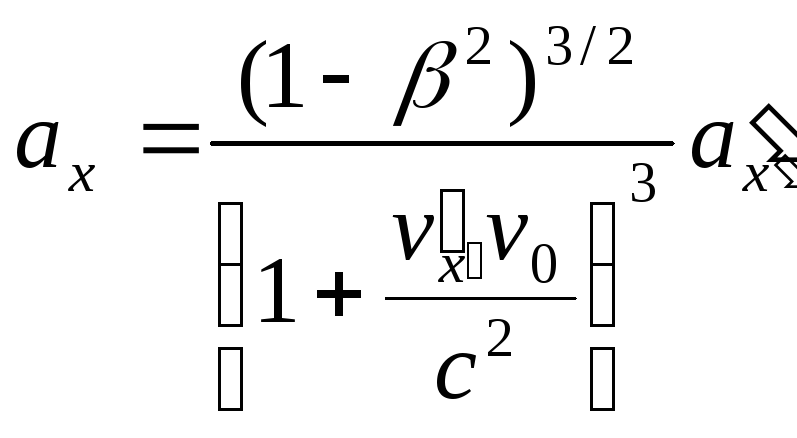. (2.19)

Компоненти прискорення і перетворюються у такий самий спосіб і дорівнюють:

(2.20)

д) Швидкості і прискорення в супроводжуючий ІСВ

Нехай в момент часу матеріальна точка в ІСВ має швидкість . Введемо ІСВ , швидкість якої відносно дорівнює :

.

В подальшому швидкість ІСВ , як і повинно бути, буде залишатись незмінною. В той же час швидкість точки буде зростати або зменшуватись і вона буде змінювати своє положення в ІСВ . Означену у такий спосіб ІСВ будемо називати супроводжуючою ІСВ (СІСВ) і позначати . Як завжди, вісь СІСВ будемо направляти вздовж , а напрямки осей і обирати із якихось додаткових міркувань. Підставляючи компоненти швидкості і прискорення точки в ІСВ в (2.18) і (2.19), (2.20) знаходимо, що їх значення у вихідній ІСВ в момент часу дорівнюють:

, (2.22)

і

. (2.21)

Для того, щоб краще зрозуміти особливості застосування СІСВ, розглянемо наступну задачу:

Точка рухається вздовж прямої з прискоренням, яке в СІСВ залишається постійним за величиною і дорівнює: . Знайти закон руху точки в лабораторній системі відліку.

Нехай вісь ЛСВ також направлена вздовж напрямку руху точки. Тоді за допомогою (2.21) для - компоненти швидкості точки отримуємо рівняння:

, .

Позначаючи тут і інтегруючи відповідне рівняння, знаходимо:

,

де позначає початковий момент часу. Враховуючи, що , рівнянню для - координати можна надати вигляд:

.

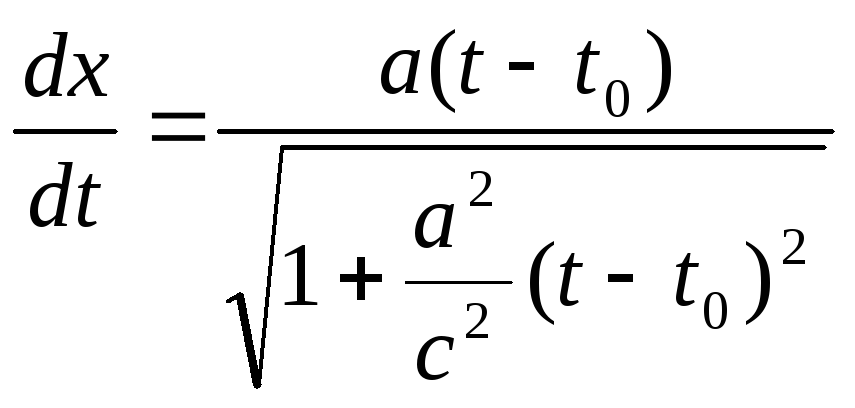Це рівняння елементарно інтегрується і приводить до наступного закону руху:

, (2.22)

де координата точки в початковий момент часу . На початку руху і після тривалого часу руху рівняння (2.22) суттєво спрощується:

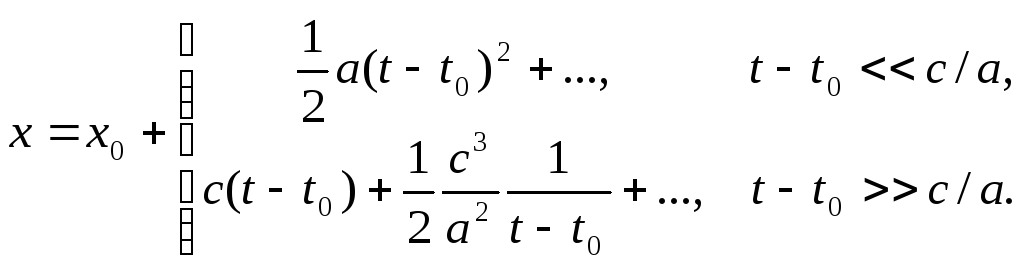
Перший граничний випадок повністю узгоджується із рівнянням руху в класичній механіці. Другий граничний випадок, як бачимо, свідчить про те, що гранична швидкість точки ніколи не перевищує швидкості світла.

е) Закон перетворення кутів

Перетворення кутів при переході від однієї ІСВ до другої є менш однозначною проблемою. Тут відповідь залежить від того, яким чином утворюється той чи інший кут. Проілюструємо цю ситуацію на двох простих випадках. Давайте розглянемо закони перетворення кутів між 1) сторонами прямокутного трикутника і 2) напрямками швидкості точки і швидкістю відносного руху ІСВ і .

Нехай, як завжди, осі і є направленими вздовж вектора швидкості відносного руху ІСВ і . Будемо вважати, що катети прямокутного трикутника лежать на осях і СК в ІСВ і мають довжини і відповідно. Тангенс кута , який утворює катет з гіпотенузою, очевидно дорівнює:

.

Знайдемо тепер відповідний кут в ІСВ . Будемо виходити з того, що довжини катетів перетворюються так само, як і довжини стержнів, зорієнтованих вздовж осей і . У згоді з цим, зразу знаходимо:

.

Шуканий кут , таким чином, задовольняє рівнянню:

. (2.23)

При кут прямує до .

Для отримання відповіді в другій задачі, ми виходимо з того, що кут , утворений швидкістю точки в ІСВ з віссю , дорівнює:

.

Відповідні значення швидкості точки в ІСВ згідно (2.18) дорівнюють:

і ,

і приводять до наступного значення кута :

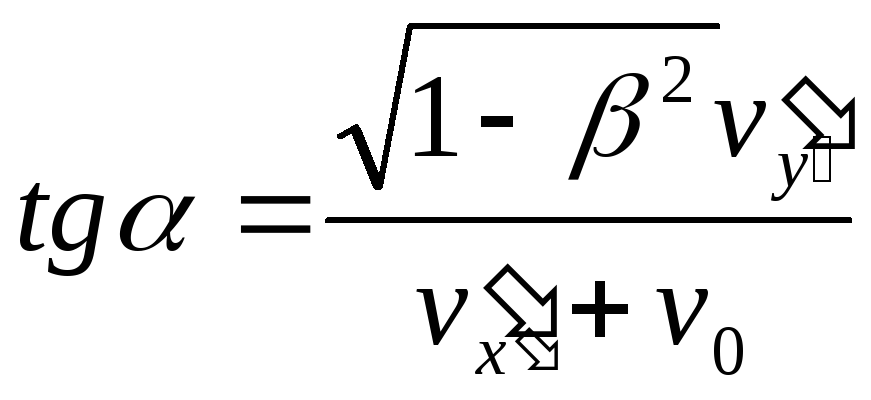. (2.24)

Якщо ввести модуль швидкості 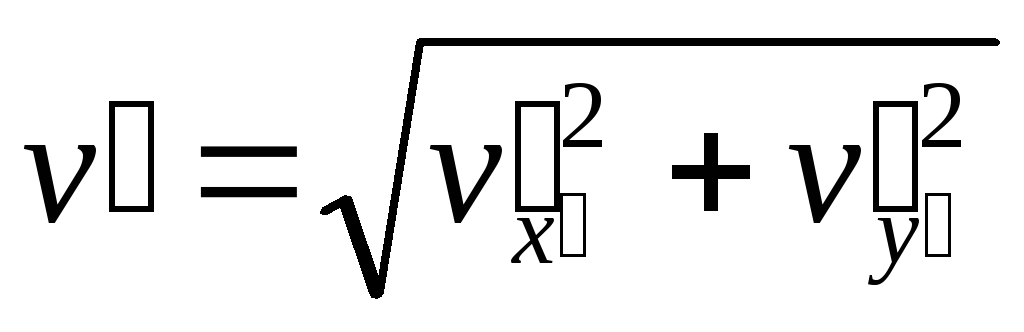, то компонентам швидкості і можна надати вигляд:

. (2.25)

Порівняння (2.23) і (2.24), (2.25) показує, що закон перетворення кута визначальним чином залежить від особливостей його утворення.

В граничному випадку, коли , прямує до граничного значення:

. (2.26)

Враховуючи, що , знаходимо також

, . (2.27)