Для студентов / Лекции / (2)ВЕД / (11)Потенціали Лієнара-Віхерта

11. Потенціали Лієнара-Віхерта

Так називають запізнілі скалярний і векторний потенціали електромагнітного поля, утвореного рухомим точковим зарядом . Нехай положення заряду описується радіус-вектором , який змінюється з часом за відомим законом. Просторовий розподіл зарядів і токів, що відповідають рухомому точковому заряду, описуються формулами:

(11.1)

Для знаходження запізнілих потенціалів достатньо вирази (11.1) підставити в формули (10.17) і (10.20), які визначають запізнілі потенціали в загальному випадку:

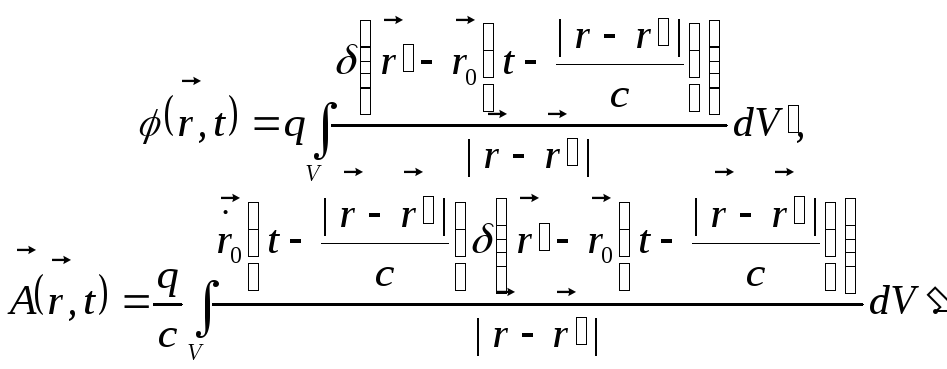(11.2)

На жаль, інтегрування за просторовою змінною в (11.2) є непростим, оскільки вона входить як в комбінації , так і в часову змінну . Саме остання обставина і унеможливлює виконання безпосереднього інтегрування за змінною .

Цю перешкоду не важко подолати, якщо звернутись до формул (10.22) і (10.28), які представляють запізнілі скалярний і векторний потенціали електромагнітного поля за допомогою функції Гріна. Так, для скалярного потенціалу знаходимо:

. (11.3)

Тут просторова змінна інтегрування входить тільки в комбінації і тому, використовуючи властивості дельта-функції Дірака (див. ()), без зусиль знаходимо наступний проміжний результат:

,

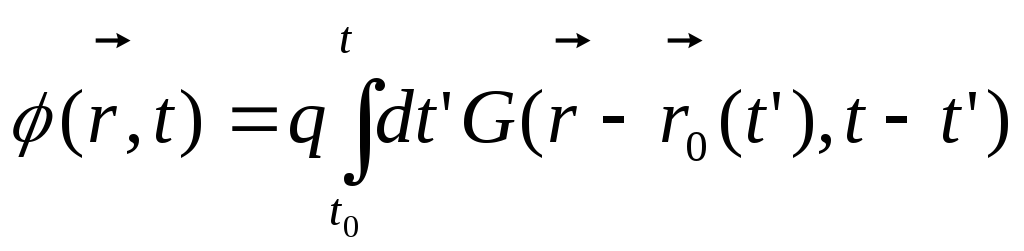де - момент початку руху заряду. З врахуванням явного вигляду функції Гріна (10.23) отримуємо:

. (11.4)

Інтеграл, який входить до (11.4), за своєю структурою є таким самим, як і інтеграли у формулах (11.2). Але він є суттєво простішим, оскільки змінна є скалярною. В той же час, до інтегралів в (11.2) входить векторна змінна , яка породжує три взаємопов’язаних скалярних змінних. Для виконання інтегрування в (11.4) зробимо заміну змінної інтегрування:

.

Їй відповідає наступний зв'язок між старим і новим диференціалами:

.

Як наслідок, формула (11.4) переписується у вигляді інтегралу:

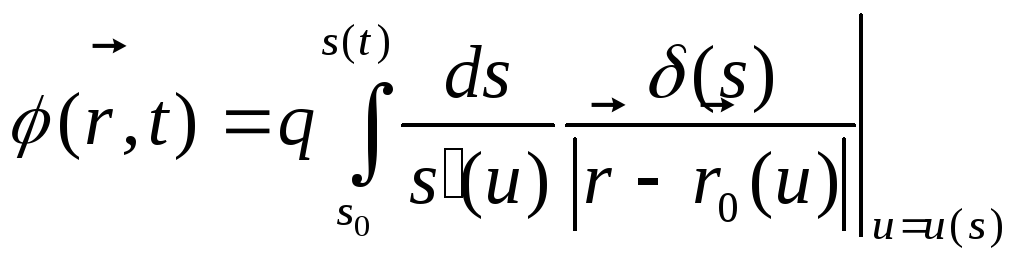, (11.5)

який вже обчислюється елементарно. Він дорівнює значенню підінтегральної функції, яка входить множником перед дельта-функцією Дірака, при :

. (11.6)

Сумування в (11.6) відбувається по всім кореням рівняння , або у більш розгорнутому вигляді:

. (11.7)

За своїм фізичним змістом, корені утворюють сукупність моментів часу випромінювання електромагнітних сигналів, які досягають точки спостереження в момент часу .

Неважко бачити, що похідна дорівнює:

,

де - швидкість заряду. Як наслідок, запізнілий скалярний потенціал рухомого точкового заряду, який дається формулою (11.6), можна переписати у більш явній формі:

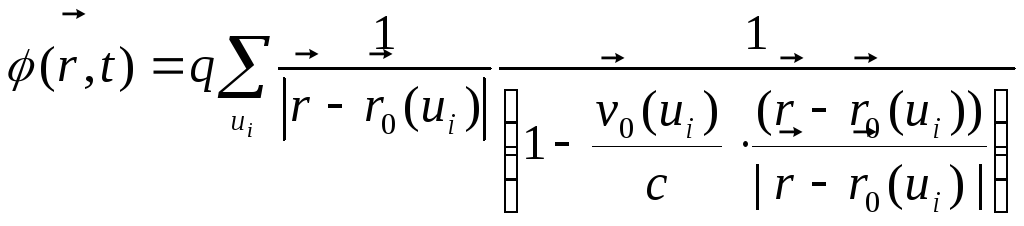. (11.8)

Як бачимо, рух заряду призводить до суттєвої зміни просторового розподілу потенціалу в його околі у порівнянні з нерухомим зарядом:

.

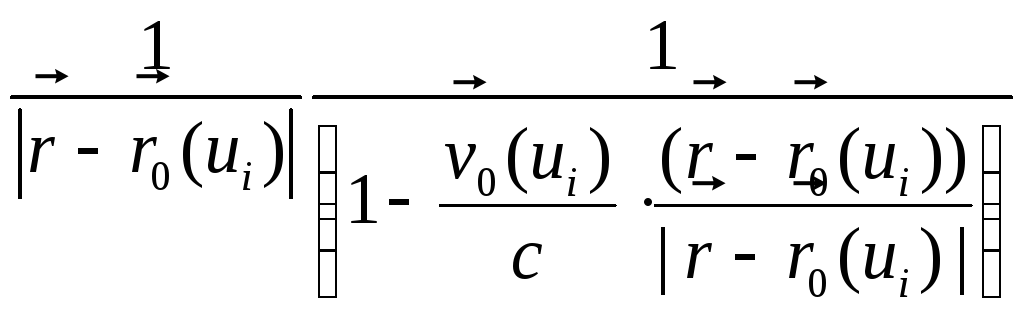Величина зміниє тим більшою, чим ближче швидкість заряду наближується до швидкості розповсюдження електромагнітного сигналу.

Запізнілий векторний потенціал рухомого точкового заряду визначається

формулою, цілком подібною до (11.8):

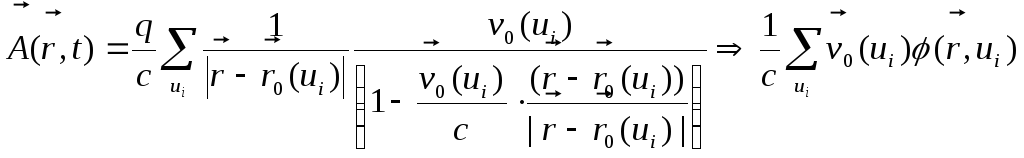, (11.9)

де

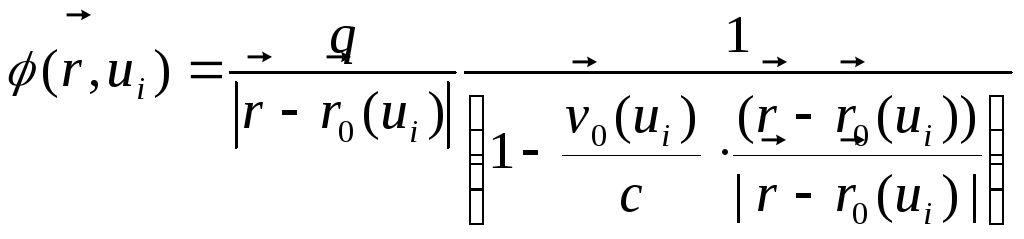. (11.10)

а) Електромагнітні потенціали точкового заряду, який рухається з постійними за величиною і напрямком швидкістю

Направимо вісь лабораторної системи координат вздовж напрямку швидкості заряду. Крім того, будемо вважати, що в початковий момент часу положення заряду збігається з початком координат. Тоді

, ,

і скалярному потенціалу електричного поля, згідно (11.8), можна надати вигляду:

,

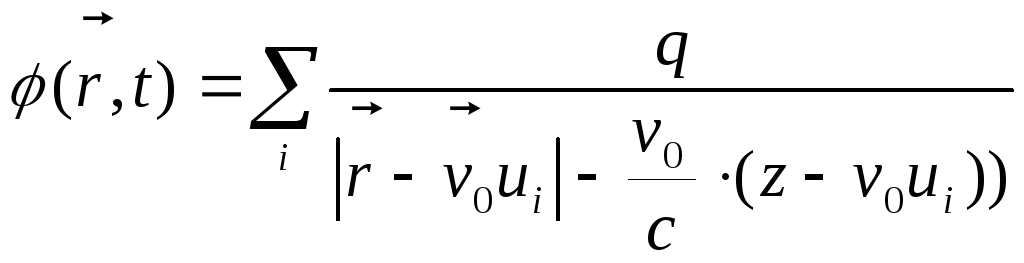де моменти випромінювання електромагнітних сигналів задовольняють квадратному рівнянню:

.

Вводячи позначення , , і , де () – компоненти радіус-вектора , два останні рівняння можна переписати у вигляді:

, (11.11)

. (11.12)

З двох коренів квадратного рівняння (11.12) фізичний смисл має тільки корінь:

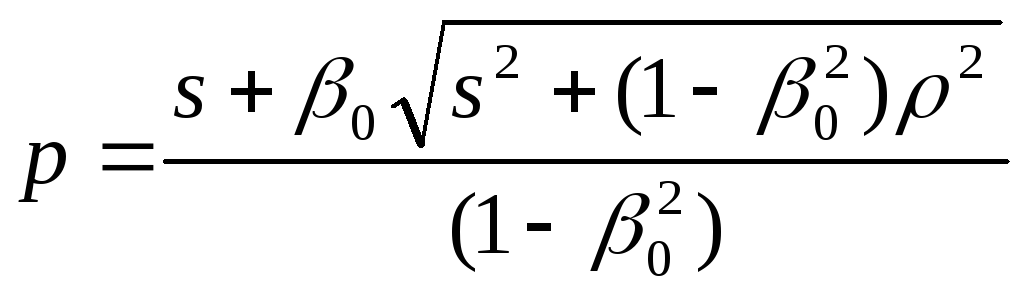. (11.13)

Другий корінь 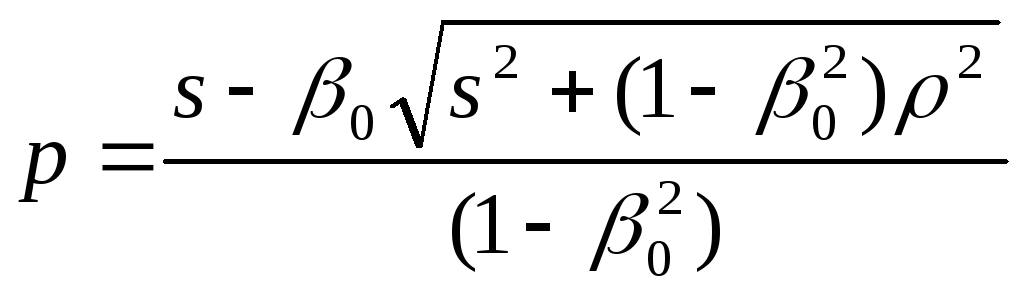при приводить до некоректної асимптотики: , оскільки при певних значеннях і її ліва частина є позитивною, а права частина при достатньо великих стає негативною. Підставляючи (11.13) в (11.11) і виконуючи громіздкі, але тривіальні, перетворення, знаходимо:

. (11.14)

У згоді з (11.9) векторний потенціал повинен дорівнювати:

. (11.15)

б) Еквіпотенціальні поверхні рухомого електричного заряду

Більш наочне уявлення про просторовий розподіл електричного поля рухомого точкового заряду ми отримаємо, коли розглянемо еквіпотенціальні поверхні, які відповідають потенціалу (11.14). Вони визначаються стандартним рівнянням:

,

яке можна представити у вигляді:

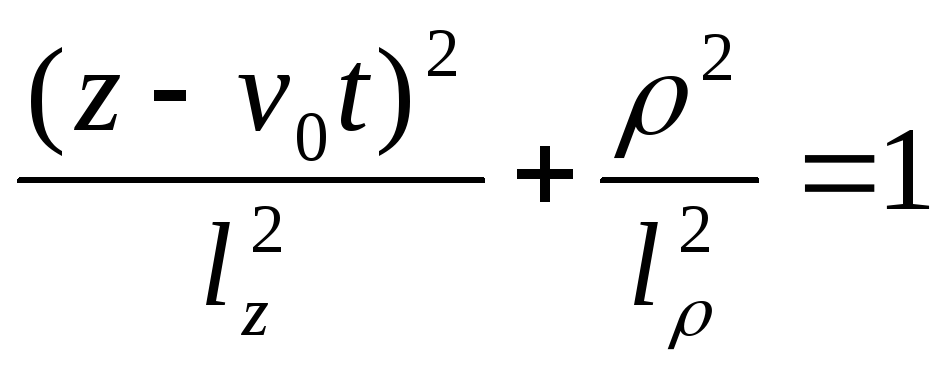. (11.16)

Це є рівняння еліпсу з півосями:

,

центр якого рухається вздовж вісі зі швидкістю . Довжина півосі не залежить від швидкості і приймає таке ж саме значення , яке є характерним для нерухомого заряду:

. (11.17)

В останньому випадку, як і повинно бути, еквіпотенціальні поверхні є сферами. Що стосується півосей еліпса вздовж і осей, то вони є однаковими () і зростають зі швидкістю заряду. Таким чином, еквіпотенціальна сфера для нерухомого заряду переходить у еквіпотенціальний еліпс обертання для заряду, який рухається з постійною за величиною і направленням швидкістю. Коли , цей еліпс за своєю формою більше нагадує оладку великого розміру або млинець.

Якщо константу змінимо на невелику величину , то довжина півосей еліпсу також зміниться:

. За означенням, компоненти і напруженостей полів в напрямку вісі і площині (), яка проходить через центр еліпсу, дорівнюють:

і .

Звідси випливає, що на одній і тій же еквіпотенціальній поверхні напруженість поля у площині () є меншою, чим у напрямку руху заряду:

.

Такі ж самі висновки можна зробити і з аналізу просторового розподілу напруженості електричного поля:

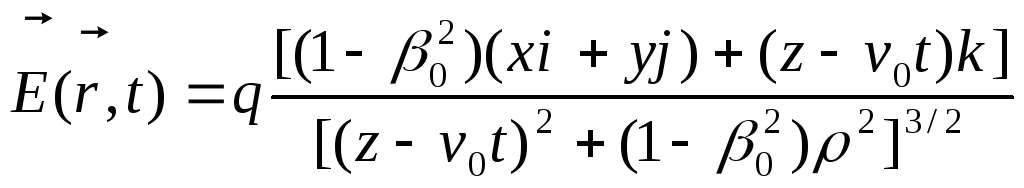(11.18)

при .

Оскільки значення напруженості поля є пропорційними густині розподілу векторних ліній, то ми приходимо до висновку, що ізотропний розподіл векторних ліній у випадку нерухомого заряду змінюється на анізотропний їх розподіл, коли заряд рухається. Густина векторних ліній зростає у напрямку руху тим більше, чим ближче швидкість заряду наближається до швидкості розповсюдження електромагнітного поля. У граничному випадку, коли , електричне поле майже повністю зосереджується всередині голко-подібних областей, які охоплюють вісь , тобто напрямок руху, в обох від заряду напрямках. Слід зазначити, що такий самий розподіл електричного поля є характерним також для заряджених частинок на їх орбітах руху в колайдерах великого радіусу.

в) Напруженість магнітного поля рухомого заряду

Виходячи з означення напруженості магнітного поля за допомогою (11.15) знаходимо:

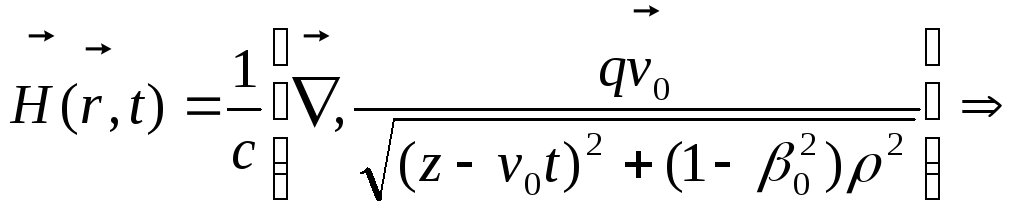
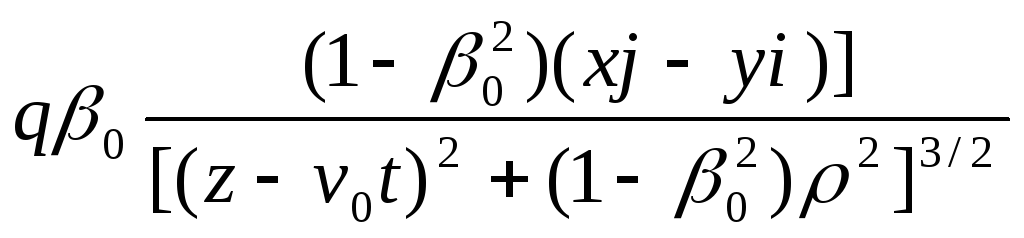. (11.19)

Тут більш зручно перейти до циліндричної системи координат, в якій . Тоді

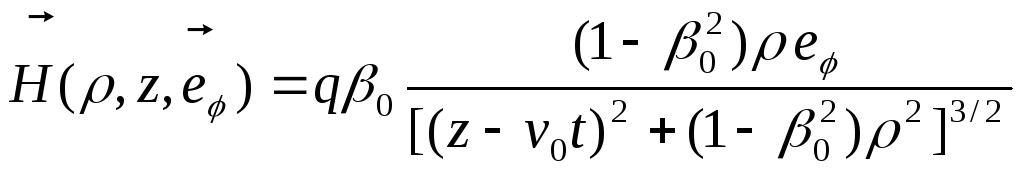. (11.20)

Як і повинно бути, векторні лінії магнітного поля є колами, які охоплюють вісь . При напруженість магнітного поля рухомого заряду прямує до нуля всюди, за виключенням області, яка прилягає до площини (), що проходить через точку . На самій цій площині змінюється за законом:

. (11.21)

Тобто, магнітне поле набуває плоско-подібного характеру. Нагадаємо, що в цьому самому граничному випадку електричне поле зосереджується в голко-подібних областях, які охоплюють вісь . Вираз для напруженості магнітного поля можна подати і в іншому вигляді, використавши формулу (11.18) для напруженості електричного поля:

. (11.22)

г) Потенціали електричного і магнітного полів рухомого заряду в більш загальній формі

Узагальнимо формули (11.14) і (11.15) на більш загальний випадок, коли заряд рухається з постійною швидкістю вздовж прямої, яка не співпадає з координатними осями і не проходить через початок координат. Крім того, в початковий момент часу заряд знаходиться в довільній точці . Фактично, узагальнення вказаних формул полягає в переході до векторних позначень.

Одне з узагальнень тут є тривіальним: . Аналогом координати у формулі (11.14) є проекція вектора на напрямок, який співпадає з напрямком швидкості заряду. Нехай цей напрямок задається одиничним вектором . Тоді . Так само, замість треба підставити . Остаточно, скалярний потенціал набуває вигляду:

. (11.23)

Векторний потенціал узагальнюється аналогічним чином:

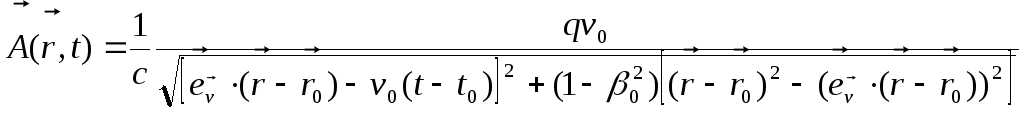. (11.24)