
Для студентов / Лекции / (2)ВЕД / (14)Розповсюдження електромагнітного поля
.doc12. Розповсюдження електромагнітного поля
Цей розділ присвячується аналізу особливостей розповсюдження електромагнітного поля в вакуумі, тобто за межами джерел, які його утворюють. Основна увага зосереджується на властивостях плоских, сферичних і циліндричних хвиль. Всі вони задовольняють однорідним хвильовим рівнянням:
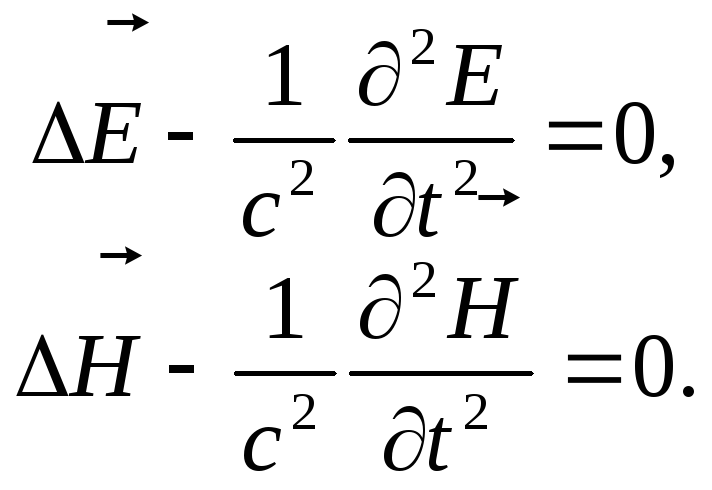 ,
(12.1)
,
(12.1)
які були побудовані в розділі 7 (див. (7.24)). В певних ситуаціях на першому кроці більш зручним виявляється аналіз особливостей розповсюдження електромагнітних потенціалів, які також задовольняють однорідним хвильовим рівнянням (див. (9.6)):
 .
(12.2)
.
(12.2)
Ми розглянемо структуру як загальних розв’язків рівнянь (12.1) і (12.2), які мають відповідну симетрію, так і найпростіші розв’язки, з яких можна побудувати довільний електромагнітний сигнал.
Зазначимо, що в загальному випадку електромагнітне збудження залежить від просторових координат і часу наступним чином:
![]() - в ДСК,
- в ДСК,
![]() - в ССК,
- в ССК,
![]() - в ЦСК.
- в ЦСК.
Тут для
ілюстрації характеру залежностей ми
використали тільки напруженість
електричного поля, хоча подібна залежність
властива і
![]() ,
,
![]() ,
,
![]() .
При наявності симетрії того чи іншого
типу, залежність від просторових
координат стає більш простою і специфічною.
Переходимо до розгляду саме таких
найбільш характерних ситуацій.
.
При наявності симетрії того чи іншого
типу, залежність від просторових
координат стає більш простою і специфічною.
Переходимо до розгляду саме таких
найбільш характерних ситуацій.
а) Плоскі електромагнітні хвилі
Просторово-часова залежність електромагнітних збуджень такого типу має характер:
![]() ,
(12.3)
,
(12.3)
де
![]() - координата, яка відраховується вздовж
вісі, напрямок якої задається ортом
- координата, яка відраховується вздовж
вісі, напрямок якої задається ортом
![]() .
Це означає, що значення напруженості
електричного і магнітного полів в
плоскій хвилі 1) є однаковими у всіх
точках довільної площини, перпендикулярної
до вісі
.
Це означає, що значення напруженості
електричного і магнітного полів в
плоскій хвилі 1) є однаковими у всіх
точках довільної площини, перпендикулярної
до вісі
![]() і 2) залежать тільки від положення
площини, тобто, координати
і 2) залежать тільки від положення
площини, тобто, координати
![]() і часу
і часу
![]() .
.
У згоді з цим можна надати наступне означення плоскої хвилі:
Плоска хвиля представляє собою електромагнітне збудження, в якому напруженості електричного і магнітного полів приймають постійні значення в площинах, перпендикулярних до напрямку розповсюдження поля.
Залежність
![]() і
і
![]() від просторових координат і часу для
таких збуджень, очевидно, описується
формулами (12.3).
від просторових координат і часу для
таких збуджень, очевидно, описується
формулами (12.3).
Нехай
![]() позначає довільну точку в якійсь з таких
площин. Відповідне значення координати
позначає довільну точку в якійсь з таких
площин. Відповідне значення координати
![]() ,
очевидно, визначається скалярним
добутком радіус-вектора
,
очевидно, визначається скалярним
добутком радіус-вектора
![]() і орта
і орта
![]() :
:
![]() .
В більш розгорнутому вигляді:
.
В більш розгорнутому вигляді:
![]() і
і
![]() .
(12.4)
.
(12.4)
Дія оператора Лапласа на вирази (12.3) для напруженості полів обчислюється за правилами диференціювання функції від складного аргументу. Таким шляхом неважко впевнитись, що
![]() ,
,
а рівняння (12.1) переходять в одномірні хвильові рівняння:
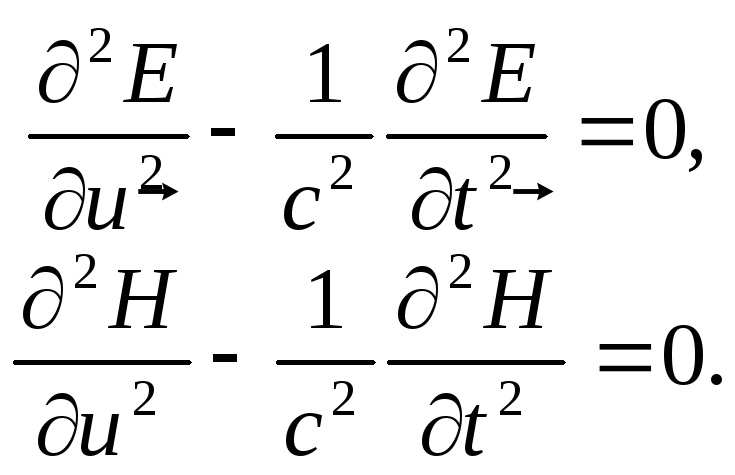 (12.5)
(12.5)
Як відомо
з курсів математичної фізики, перехід
до нових змінних:
![]() і
і
![]() ,
вперше використаних Д’Аламбером,
дозволяє рівняння (12.5) переписати у
вигляді:
,
вперше використаних Д’Аламбером,
дозволяє рівняння (12.5) переписати у
вигляді:
![]() .
(12.6)
.
(12.6)
Їх загальний розв’язок має структуру:
![]() ,
,
де
![]() ,
,
![]() ,
а також
,
а також
![]() ,
незалежні
функції. Після повернення до вихідних
змінних ми отримуємо:
,
незалежні
функції. Після повернення до вихідних
змінних ми отримуємо:
![]() .
(12.7)
.
(12.7)
Кожний
з доданків в (12.7) відповідає хвилям, які
розповсюджуються вздовж вісі
![]() зі швидкістю
зі швидкістю
![]() .
Дійсно, довільні фіксовані значення
напруженостей електричного і магнітного
полів , які відповідають хвилі від
аргументу
.
Дійсно, довільні фіксовані значення
напруженостей електричного і магнітного
полів , які відповідають хвилі від
аргументу
![]() ,
спостерігаються в точках
,
спостерігаються в точках
![]() і
і
![]() ,
які залишають комбінацію
,
які залишають комбінацію
![]() незмінною:
незмінною:
![]() ,
,
де
![]() і
і
![]() є
деякі константи. Цю комбінацію прийнято
називати фазою хвилі. Бачимо, що фіксовані
значення напруженостей полів зміщуються
вздовж вісі
є
деякі константи. Цю комбінацію прийнято
називати фазою хвилі. Бачимо, що фіксовані
значення напруженостей полів зміщуються
вздовж вісі
![]() зі швидкістю
зі швидкістю
![]() :
:
![]() .
(12.8)
.
(12.8)
Так само
хвиля, просторово-часова еволюція якої
визначається комбінацією
![]() ,
відповідає хвилі, що розповсюджується
в зворотному напрямку:
,
відповідає хвилі, що розповсюджується
в зворотному напрямку:
![]() .
(12.9)
.
(12.9)
Розглянемо
тепер більш детально властивості плоскої
хвилі, яка розповсюджується вздовж вісі
![]() .
Підставимо
.
Підставимо
![]() і
і
![]() в
рівняння Максвела:
в
рівняння Максвела:
 (12.10)
(12.10)
Неважко
впевнитись, що
![]() ,
завдяки чому перше і третє рівняння в
(12.10) переписуються у вигляді:
,
завдяки чому перше і третє рівняння в
(12.10) переписуються у вигляді:
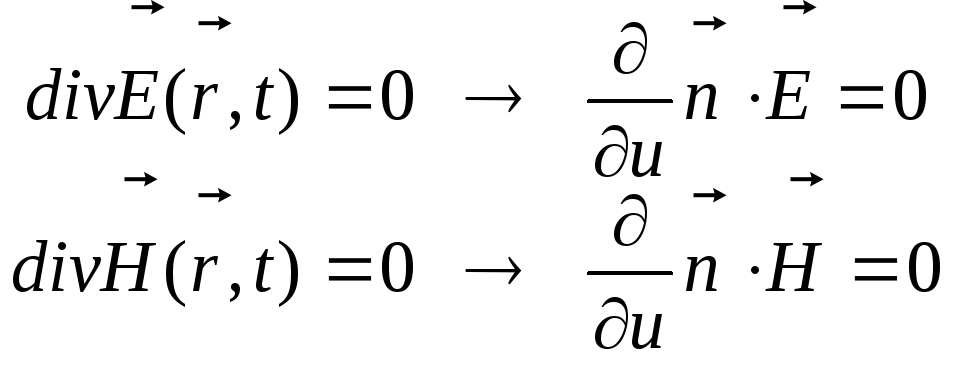 .
(12.11)
.
(12.11)
Звідси
випливає що
![]() і
і
![]() ,
де
,
де
![]() і
і
![]() - довільні константи, значення яких не
повинні залежати від напруженості
полів. Ці співвідношення повинні мати
місце і в сильних, і в гранично слабких
полях. Зрозуміло, що це можливо тільки
при умовах:
- довільні константи, значення яких не
повинні залежати від напруженості
полів. Ці співвідношення повинні мати
місце і в сильних, і в гранично слабких
полях. Зрозуміло, що це можливо тільки
при умовах:
![]() і
і
![]() ,
(12.12)
,
(12.12)
які засвідчують, що плоскі електромагнітні хвилі є поперечними, тобто вектори напруженості електричного і магнітного полів лежать у площинах, перпендикулярних до напрямку розповсюдження хвилі.
Можна також перевірити, що для обох типів хвиль
![]() ,
,
і
![]() .
.
Відповідні похідні від напруженості магнітного поля мають таку саму структуру. Це дозволяє друге і четверте рівняння в (12.10) представити у вигляді:
![]() і
і
![]() .
.
По тій же причині, що і при виведенні рівнянь (12.12), звідси випливає:
![]() і
і
![]() .
(12.13)
.
(12.13)
З фізичної
точки зору, це означає, що 1) вектори
![]() утворюють трійку взаємно перпендикулярних
векторів і 2) вектори
утворюють трійку взаємно перпендикулярних
векторів і 2) вектори
![]() і
і
![]() змінюються синфазно у просторі і з
часом, тобто, мінімумам і максимумам
одного поля відповідають мінімуми і
максимуми другого поля.
змінюються синфазно у просторі і з
часом, тобто, мінімумам і максимумам
одного поля відповідають мінімуми і
максимуми другого поля.
Для
хвилі
![]() ,
яка розповсюджується в зворотному
напрямку, співвідношення типу (12.13)
відрізняються знаками:
,
яка розповсюджується в зворотному
напрямку, співвідношення типу (12.13)
відрізняються знаками:
![]() і
і
![]() .
(12.14)
.
(12.14)
Це стає цілком зрозумілим, якщо врахувати, що її напрямку розповсюдження
відповідає
вектор
![]() .
При врахуванні цієї обставини
співвідношення (12.14) стає повністю
еквівалентним (12.13).
.
При врахуванні цієї обставини
співвідношення (12.14) стає повністю
еквівалентним (12.13).
Зазначимо, що всі ці висновки, зроблені на основі рівнянь Максвела, повністю узгоджуються з експериментальними даними.
б) Плоскі монохроматичні хвилі
Окремим
випадком плоских хвиль є монохроматичні
плоскі хвилі. Так прийнято називати
хвилі, в яких просторово-часова еволюція
електро-магнітного поля має осциляційний
характер, тобто відбувається за законами
косинуса або синуса. Оскільки синусоїдальна
залежність відрізняється від
косинусоїдальної тільки зсувом аргументу
на
![]() ,
то ми будемо використовувати, як правило,
закон косинуса:
,
то ми будемо використовувати, як правило,
закон косинуса:
![]() ,
,
![]() ,
(12.15)
,
(12.15)
де
![]() і
і
![]() - постійні вектори, які називають
амплітудами хвиль,
- постійні вектори, які називають
амплітудами хвиль,
![]() - циклічна частота. Додатковий множник
- циклічна частота. Додатковий множник
![]() розмірності оберненої швидкості введено
для утворення безрозмірної комбінації
під знаком косинуса. При
розмірності оберненої швидкості введено
для утворення безрозмірної комбінації
під знаком косинуса. При
![]()
![]() .
Аргументи косинусів в (12.15) часто подаються
в більш загальній формі:
.
Аргументи косинусів в (12.15) часто подаються
в більш загальній формі:
![]() ,
,
де вектор
![]() прийнято називати хвильовим вектором.
Тоді формули (12.15) набувають вигляду:
прийнято називати хвильовим вектором.
Тоді формули (12.15) набувають вигляду:
![]() ,
,
![]() .
(12.16)
.
(12.16)
Дуже часто в конкретних обчисленнях використовується комплексна форма представлення:
![]() ,
,
![]() .
(12.17)
.
(12.17)
Оскільки фізичний смисл мають тільки дійсні величини, то вважається, що на останньому кроці, після всіх проміжних перетворень, потрібно виділяти дійсну частину від комплексних функцій.
в) Поляризація плоских хвиль
Розглянемо
тепер більш детально питання про напрямки
напруженостей електричного і магнітного
полів у плоских хвилях. Будемо розглядати
тільки хвилю
![]() ,
оскільки аргументація для зворотної
хвилі є цілком аналогічною. Введемо у
площині, перпендикулярній до вісі
,
оскільки аргументація для зворотної
хвилі є цілком аналогічною. Введемо у
площині, перпендикулярній до вісі
![]() ,
два взаємно перпендикулярних орти
,
два взаємно перпендикулярних орти
![]() і
і
![]() .
Тоді напруженість хвилі
.
Тоді напруженість хвилі
![]() можна представити у вигляді суми двох
незалежних хвиль:
можна представити у вигляді суми двох
незалежних хвиль:
![]() .
(12.18)
.
(12.18)
Зрозуміло,
що напрямок результуючої хвилі
![]() буде
залежати від поведінки функцій
буде
залежати від поведінки функцій
![]() і
і
![]() .
Якщо
.
Якщо
![]() і
і
![]() ,
то напрямок результуючої хвилі буде
залишатись незмінним:
,
то напрямок результуючої хвилі буде
залишатись незмінним:
![]() .
(12.19)
.
(12.19)
Таку хвилю прийнято називати плоско-поляризованою.
Якщо
![]() і
і
![]() ,
то напрямок результуючої монохроматичної
хвилі
,
то напрямок результуючої монохроматичної
хвилі
![]() (12.20)
(12.20)
буде обертатись проти ходу годинникової стрілки. Хвилю такого типу називають циркулярно-поляризованою.
Якщо
![]() і
і
![]() ,
то хвилю
,
то хвилю
![]() (12.21)
(12.21)
називають еліптично-поляризованою.
При переході до комплексного представлення плоско-, циркулярно- і еліптично-поляризованих хвиль ми враховуємо, що
 .
.
Тоді, формули (12.19) – (12.21) переписуються у вигляді:
![]() - плоска
поляризація,
- плоска
поляризація,
![]() -
циркулярна поляризація, (12.22)
-
циркулярна поляризація, (12.22)
![]() -
еліптична поляризація.
-
еліптична поляризація.
г) Сферичні електромагнітні хвилі
Для
встановлення структури найпростіших
сферичних електромагнітних хвиль,
скористаємось явним виглядом потенціалів
поля на великих відстанях від компактної
системи зарядів і токів, тобто на
відстанях
![]() ,
де
,
де
![]() -
діаметр системи. В цьому випадку система
може розглядатись як точкова, а її
електромагнітне поле, як утворене
сукупністю точкових мультипольних
моментів. Просторово-часова залежність
електромагнітних потенціалів і
напруженостей електромагнітного поля,
утворених точковими мультиполями,
визначається комбінацією:
-
діаметр системи. В цьому випадку система
може розглядатись як точкова, а її
електромагнітне поле, як утворене
сукупністю точкових мультипольних
моментів. Просторово-часова залежність
електромагнітних потенціалів і
напруженостей електромагнітного поля,
утворених точковими мультиполями,
визначається комбінацією:
![]() ,
в якій явно враховуються ефект запізнення
сигналу (
,
в якій явно враховуються ефект запізнення
сигналу (![]() ).
У згоді з (10.30) і (10.32), головні внески в
скалярний і векторний потенціали мають
структуру:
).
У згоді з (10.30) і (10.32), головні внески в
скалярний і векторний потенціали мають
структуру:
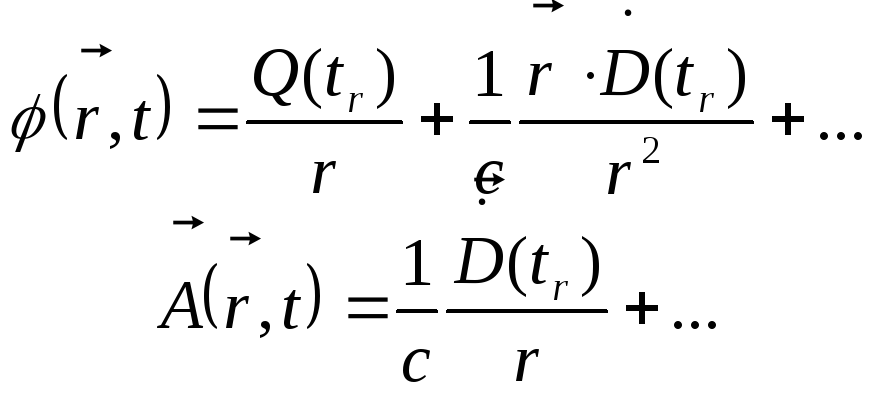 (12.23)
(12.23)
де
![]() і
і
![]() позначають заряд і дипольний момент
системи, а
позначають заряд і дипольний момент
системи, а
![]() .
Підставляючи значення потенціалів
(12.23) в формули:
.
Підставляючи значення потенціалів
(12.23) в формули:
![]() і
і
![]() ,
неважко впевнитись, що напруженості
електричного і магнітного полів
визначаються співвідношеннями:
,
неважко впевнитись, що напруженості
електричного і магнітного полів
визначаються співвідношеннями:
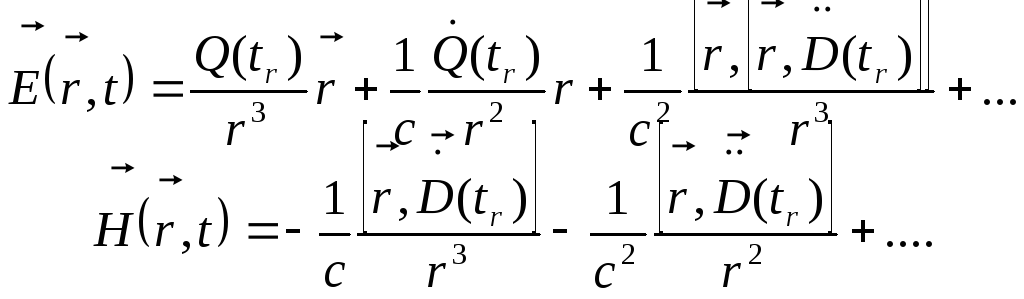 (12.24)
(12.24)
В
подальшому природно накласти вимогу
про незалежність заряду системи від
часу, що приводить до
![]() .
Крім того, будемо утримувати в (12.24)
тільки внески, які мають максимальний
порядок величини, тобто убувають за
законом
.
Крім того, будемо утримувати в (12.24)
тільки внески, які мають максимальний
порядок величини, тобто убувають за
законом
![]() :
:
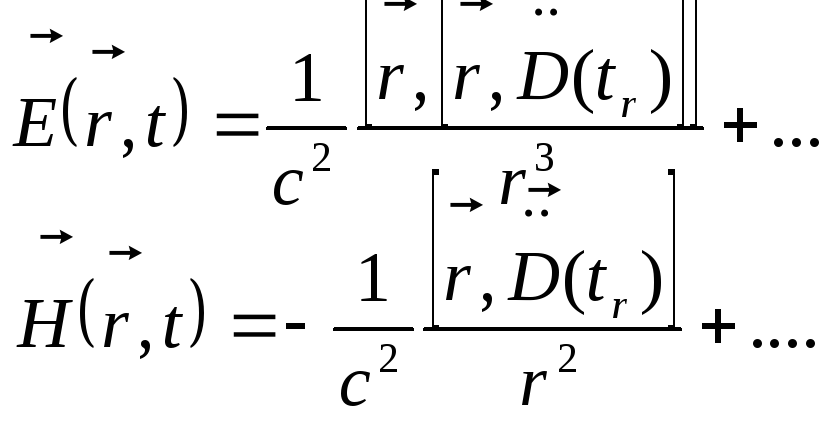 (12.25)
(12.25)
Неважко бачити, що
![]() ,
,
![]() ,
,
![]() ,
,
і
![]() .
.
З цих співвідношень випливає, що
1) вектори
![]() ,
,
![]() і
і
![]() утворюють
трійцю взаємно перпендикулярних
векторів, подібну до тієї, яку утворюють
орт
утворюють
трійцю взаємно перпендикулярних
векторів, подібну до тієї, яку утворюють
орт
![]() ,
що задає напрямок розповсюдження, і
напруженості полів для плоскої
електромагнітної хвилі. Подібно до
останньої вектори
,
що задає напрямок розповсюдження, і
напруженості полів для плоскої
електромагнітної хвилі. Подібно до
останньої вектори
![]() і
і
![]() змінюються синфазно, а їх модулі
дорівнюють один одному;
змінюються синфазно, а їх модулі
дорівнюють один одному;
2)
просторово-часова залежність сигналу
визначається комбінацією
![]() ,
де
,
де
![]() є константою розмірності часу, тобто
фронт хвилі віддаляється від системи
зарядів і токів за законом
є константою розмірності часу, тобто
фронт хвилі віддаляється від системи
зарядів і токів за законом
![]() ;
;
3) модулі
напруженостей полів при віддалені від
центру зменшуються за законом
![]() .
.
Локальна подібність властивостей електромагнітних полів в плоскій і сферичній хвилях є цілком очікуваною. Але глобально хвилі суттєво відрізняються одна від одної: в першому випадку фронт хвилі є плоским, а в другому – сферичним (на достатньо великих відстанях від компактної системи, яка їх утворює).
Розглянемо
тепер структуру сферичних хвиль в ССК.
Нехай полярна вісь ССК співпадає з
напрямком вектора
![]() .
В змінних ССК його напрямок визначається
комбінацією:
.
В змінних ССК його напрямок визначається
комбінацією:
![]() .
.
Оскільки
![]() ,
то
,
то
 (15.26)
(15.26)
Формули
(15.26) відповідають дуже простій будові
сферичних хвиль: вектори напруженостей
електричного і магнітного полів за
своїм напрямком співпадають з напрямками
дотичних до меридіану і паралелі, які
проходять через довільну точку на
сферичній поверхні. Модулі
![]() і
і
![]() мають
однакову величину. Таку ж саму структуру
повинні мати і найпростіші сферичні
хвилі, які збігаються до центру:
мають
однакову величину. Таку ж саму структуру
повинні мати і найпростіші сферичні
хвилі, які збігаються до центру:
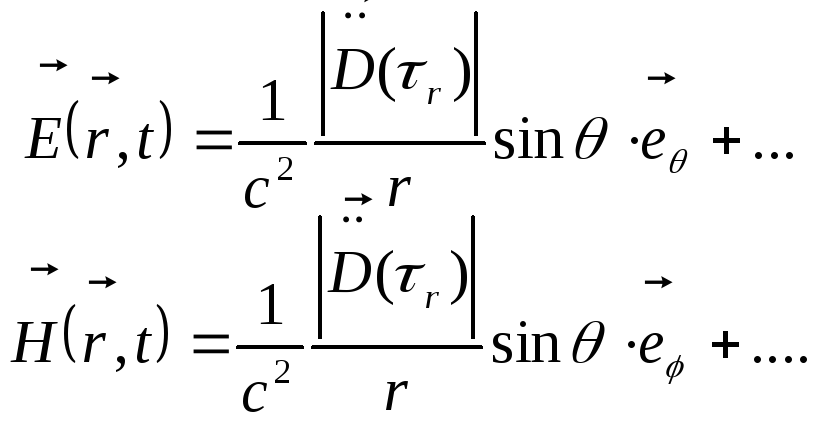 ,
(15.27)
,
(15.27)
де
![]() .
.
в) Вісесиметричні циліндричні електромагнітні хвилі
Тут ми скористаємось загальним методом, який міг бути застосованим і в попередніх випадках. Будемо шукати розв’язок хвильового рівняння для векторного потенціалу
![]() ,
(15.28)
,
(15.28)
у вигляді
![]() ,
де
,
де
![]() - орт ЦСК, направлений вздовж вісі
симетрії. Неважко впевнитись, що при
- орт ЦСК, направлений вздовж вісі
симетрії. Неважко впевнитись, що при
![]() функція
функція
![]() ,
(15.29)
,
(15.29)
задовольняє рівнянню:
![]() (15.30)
(15.30)
де
![]() .
Переходячи від
.
Переходячи від
![]() до безрозмірної змінної
до безрозмірної змінної
![]() ,
ми отримуємо рівняння
,
ми отримуємо рівняння
![]() ,
,
яке співпадає з рівнянням для нульової функції Бесселя. На цій основі ми знаходимо, що
![]() .
.
Остаточно, векторний потенціал електромагнітного поля, яке має осьову симетрію, приймає наступний вигляд:
![]() .
(15.31)
.
(15.31)
Звідси
і формул
![]() і
і
![]() випливає, що напруженості поля дорівнюють:
випливає, що напруженості поля дорівнюють:
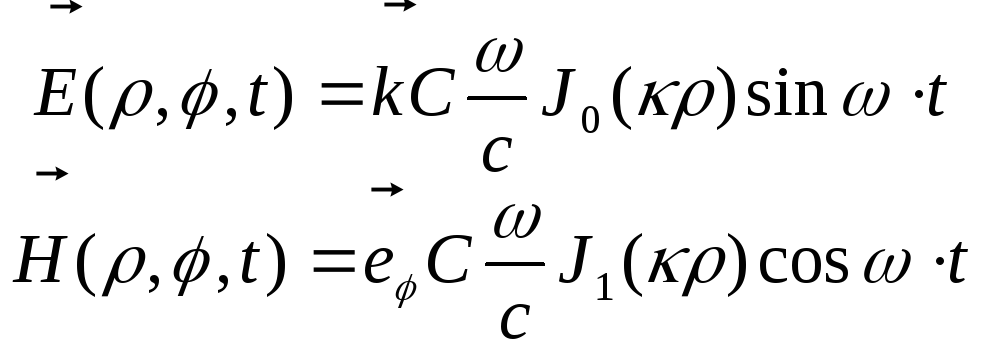 (15.32)
(15.32)
На достатньо великих відстанях від вісі симетрії функції Бесcеля мають асимптотики:
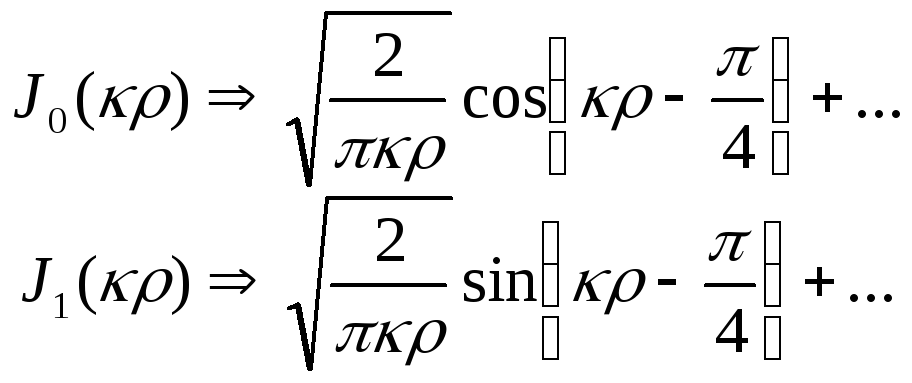 (15.33)
(15.33)
Комбінуючи (15.32) і (15.33), знаходимо наступні асимптотики напруженостей електричного і магнітного полів:
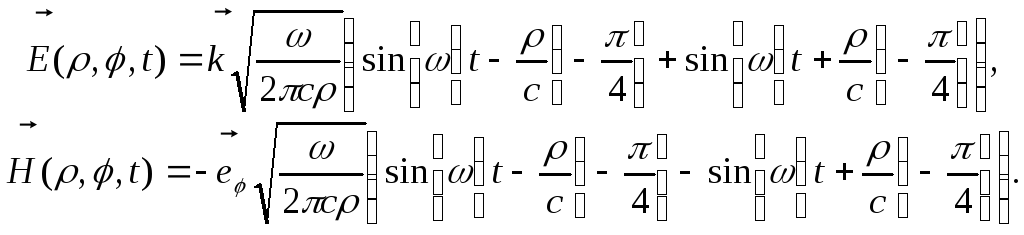 (15.34)
(15.34)
На достатньо далеких відстанях від вісі симетрії циліндричні електромагнітні хвилі, як бачимо, є локально плоскими, тобто для хвиль, що розбігаються, напруженості полів задовольняють наступним співвідношенням ортогональності:
![]() і
і
![]() .
.
В загальному випадку, напруженості електричного і магнітного полів в циліндричних хвилях є суперпозиціями хвиль (15.32), тобто мають вигляд:
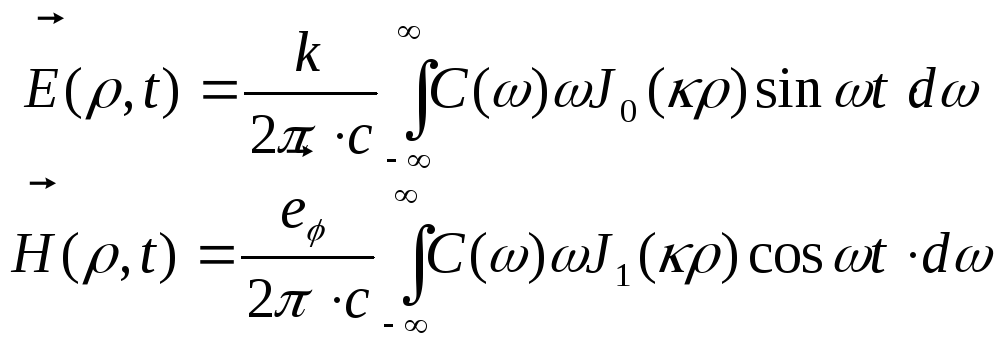 ,
(15.35)
,
(15.35)
де
![]() - довільна функція частоти. В конкретних
задачах її вигляд визначається початковими
і граничними умовами.
- довільна функція частоти. В конкретних
задачах її вигляд визначається початковими
і граничними умовами.
г) Застосування загального методу для плоских і сферичних хвиль
Напруженості електричного і магнітного полів у плоскій хвилі можна представити у вигляді:
![]() ,
,
![]() .
.
Функції
![]() і
і
![]() задовольняють рівнянням Гельмгольца:
задовольняють рівнянням Гельмгольца:
![]() ,
,
![]() .
.
і мають структуру:
![]() .
.
Комбінуючи () і (), отримуємо:
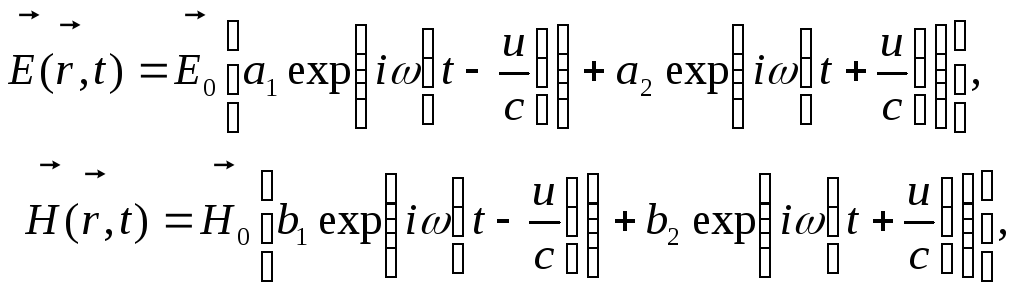
або
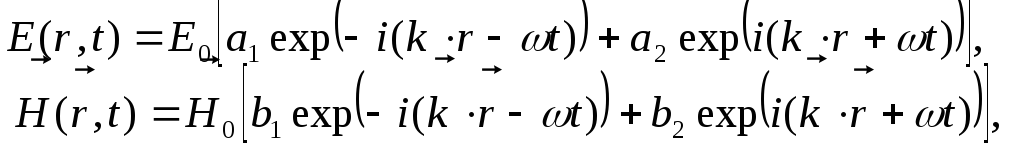
Загальний вигляд плоских хвиль визначається формулами:
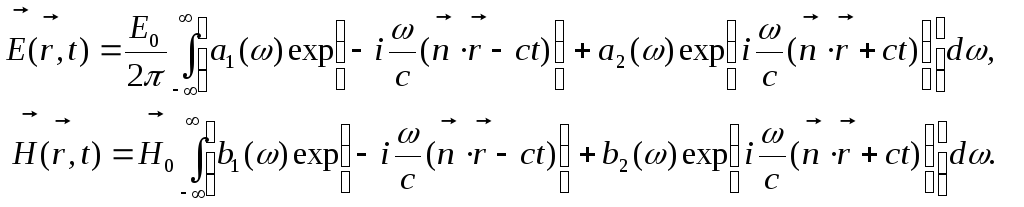 (12.36)
(12.36)
Сферичні хвилі будуються цілком аналогічним чином.
