Для студентов / (1)Векторы / (10)Ротор векторного поля в криволінійних координатах

Ротор векторного поля в криволінійних координатах

Для знаходження явного вигляду в криволінійних координатах будемо виходити з виразу , який є коректним в довільній СК. В криволінійних координатах оператор набла мають структуру (див.()):

,

а вектор представляється у вигляді: або . Розглянемо результат обчислення в обох цих випадках.

а) Контраваріантні компонент

Згідно означення , ми отримуємо:

. (13.1)

Врахуємо, що

,

де - символи Кристофеля (див. ()). Підставляючи цей вираз для похідної від базисного вектора в (13.1) і замінюючи індекси, по яким відбувається сумування, знаходимо:

. (13.2)

Оскільки векторний добуток також є вектором, його можна представити у вигляді лінійної комбінації векторів , які утворюють базис криволінійної СК: . Коефіцієнти розкладу разом з компонентами метричного тензору є незалежними характеристиками криволінійної СК. Їх прийнято називати структурними коефіцієнтами криволінійної СК. Як наслідок, можна надати вигляд:

. (13.3)

Для знаходження контраваріантних компонентів достатньо обидві частини (13.3) помножити скалярним чином на вектор . Враховуючи, що , остаточно знаходимо:

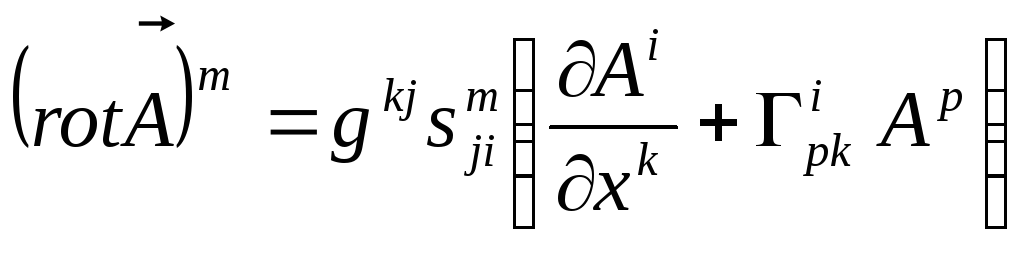. (13.4)

Бачимо, що поява додаткових коефіцієнтів в (13.3) і (13.4) суттєво ускладнює розрахунки в криволінійних СК. Але перехід до коваріантних компонентів векторного поля і приводить до суттєвого спрощення ситуації.

б) Коваріантні компонентів

В цьому випадку

. (13.5)

В розділі () було встановлено, що

,

завдяки чому вираз (13.5) для приймає вигляд:

. (13.6)

Оскільки символи Кристофеля є симетричними відносно перестановок

нижніх індексів: , то . На останньому

кроці було враховано, що зміна порядку векторів під знаком векторного добутку приводить тільки до зміни його знаку на протилежний. Як наслідок,

формула (13.6) значно спрощується:

. (13.7)

Додамо до (13.7) такий самий вираз, в якому змінено порядок розташування німих індексів. У такий спосіб знаходимо:

.

Тут скористаємось тим, що векторний добуток представити лінійною комбінацією базисних векторів:

,

завдяки чому коваріантні компоненти набувають вигляду:

, (13.8)

де

. (13.9)

Вираз (13.8) є дуже близьким до відповідного виразу в ДСК.

б) в ДСК

Добре відомо, що компоненти в тривимірній ДСК дорівнюють:

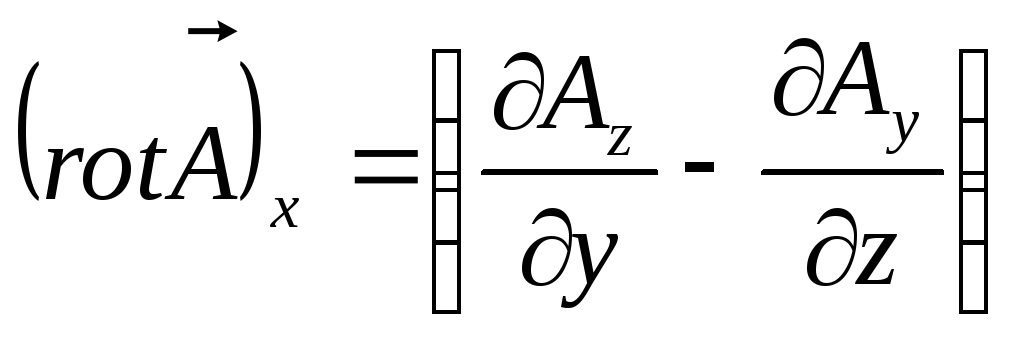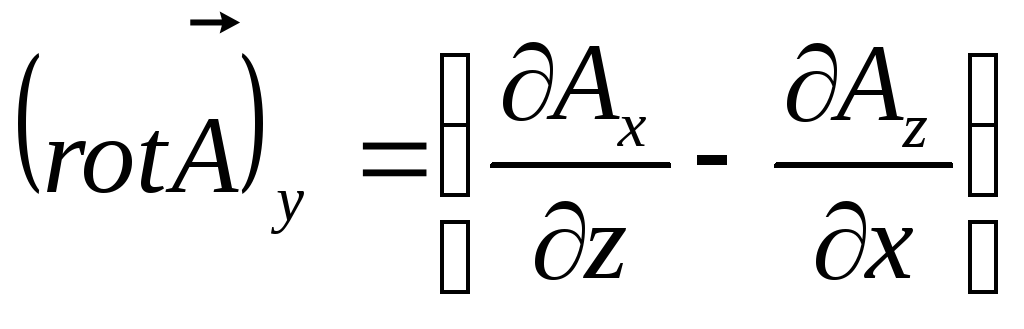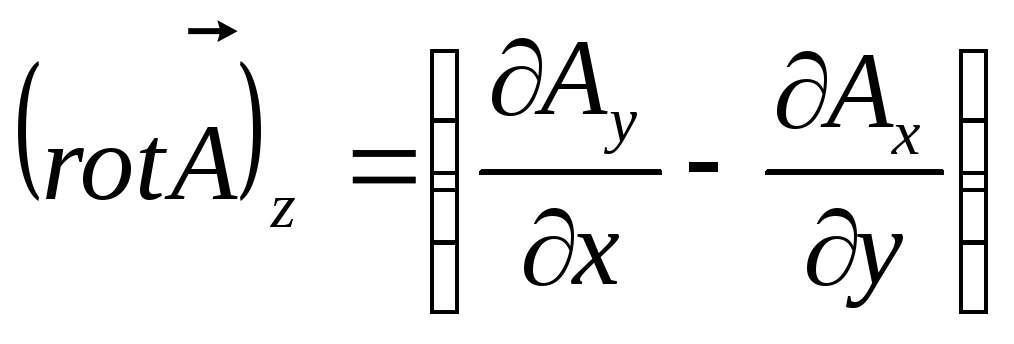, , , (13.10)

Порівняємо їх з компонентами, які відповідають (13.8). Врахуємо, що в ДСК . Як наслідок,

,

де є повністю антисиметричний тензор третього рангу. Підставляючи його в (13.8), отримуємо:

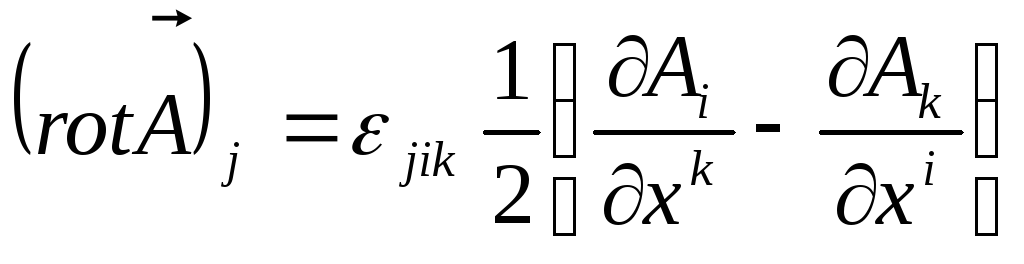, (13.11)

що є повністю еквівалентним (13.10) (множник ½ втрачається завдяки властивостям перестановочної симетрії тензора ).

Антисиметричний тензор

, (13.12)

пов'язаний з компонентами в ДСК співвідношенням (13.11) прийнято називати дуальним до вектора . Зрозуміло, що завихрення векторного поля можна з рівним успіхом описувати як за допомогою вектора , так і дуального до нього антисиметричного тензора .

Наш аналіз показує, що компоненти тензора відтворюють завихрення векторного поля і в загальному випадку, оскільки вони відповідають коваріантним компонентам в криволінійній СК (див. (13.11)).

а) Теорема Стокса

За звичай, теорема Стокса формулюється для векторних полів (див. ()):

.

Переходячи до компонентів, цю формулу в ДСК можна переписати у вигляді:

, (13.13)

де компоненти векторного елемента площини дорівнюють:

. (13.14)

Використовуючи тепер співвідношення (13.10) і означення (13.12), ліву частину формули (13.13) можна подати у змішаних векторно-тензорних змінних:

.

Права частина цієї формули стає згорткою двох антисиметричних тензорів, якщо тензорні елементи площі утворити за правилом:

. (13.15)

Тоді

.

Остаточно формула (13.13) набуває вигляду:

. (13.16)

Для переходу від ДСК до довільної криволінійної СК надамо формулі (13.15) більш загального вигляду. Оскільки в ДСК , то . В довільній криволінійній СК останнє рівняння можна переписати, зокрема, у вигляді:

Завдяки цьому,

. (13.17)