Для студентов / Методички / (1)Методичка - ВЕД / ЧI_Р5

РОЗДІЛ 5. МАГНІТОСТАТИКА

5.1 Основні методи точного розв’язування задач магнітостатики

1. Безпосереднє підсумування.

Векторний потенціал визначається виразом:

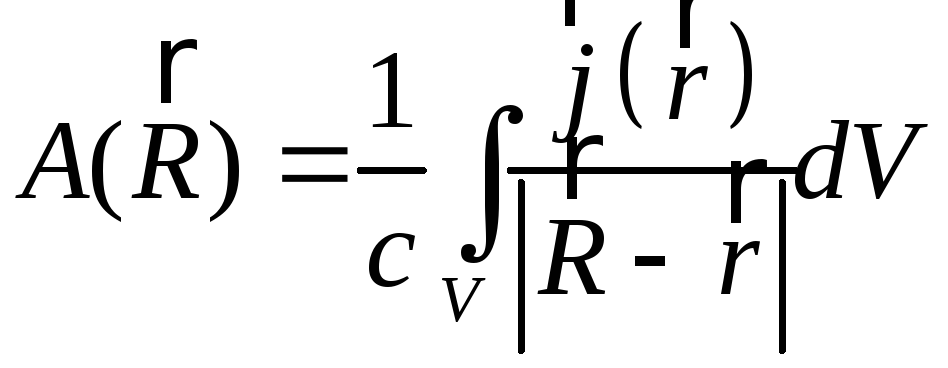. (5.1)

Напруженість магнітного поля, пов'язана з формулою:

. (5.2)

Можна, також, використовувати закон Біо-Савара, згідно з яким

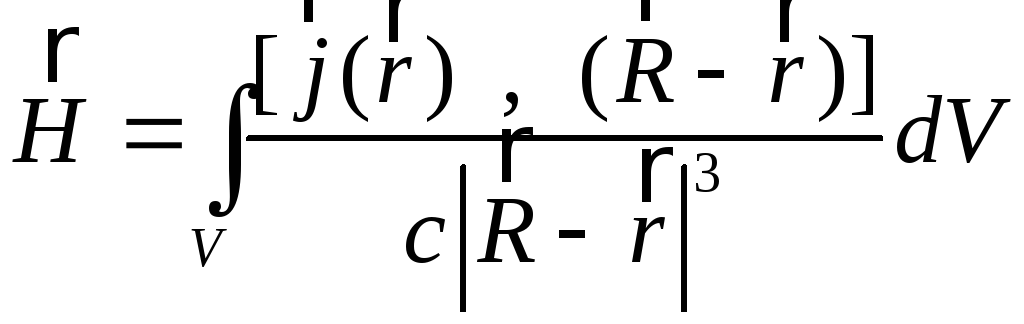(5.3)

для неперервно розподілених токів, або

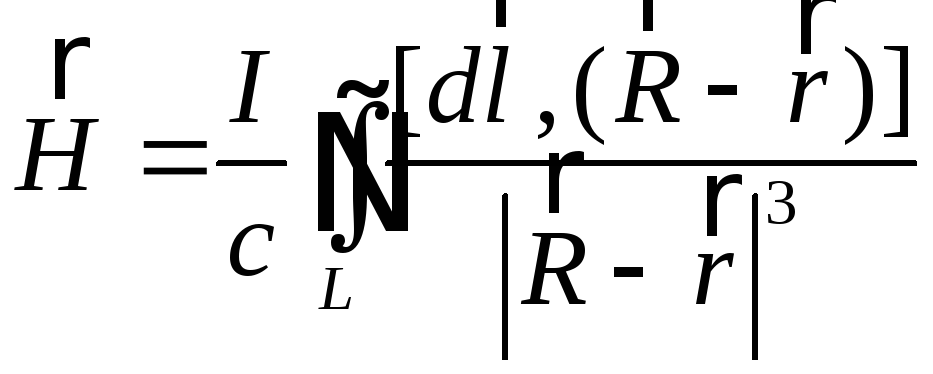(5.4)

для лінійних токів.

2. Для симетричних систем доцільно використовувати теорему про цирку-

ляцію вектора напруженості магнітного поля:

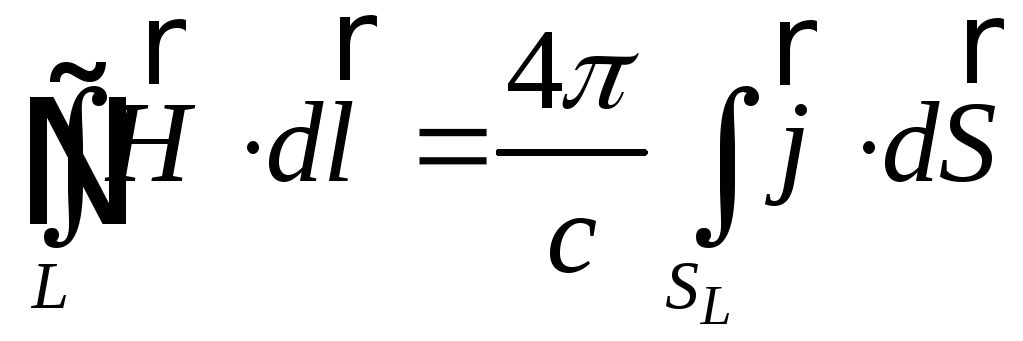. (5.5)

3. Інтегрування рівняння Пуассона:

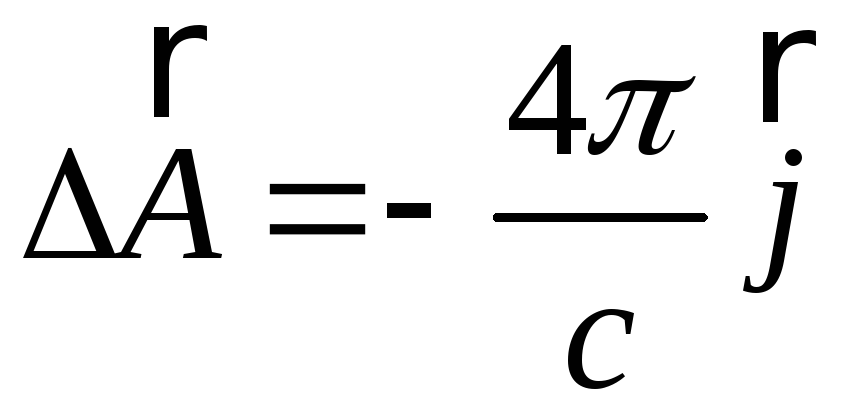. (5.6)

3. Інтегрування рівнянь Максвела:

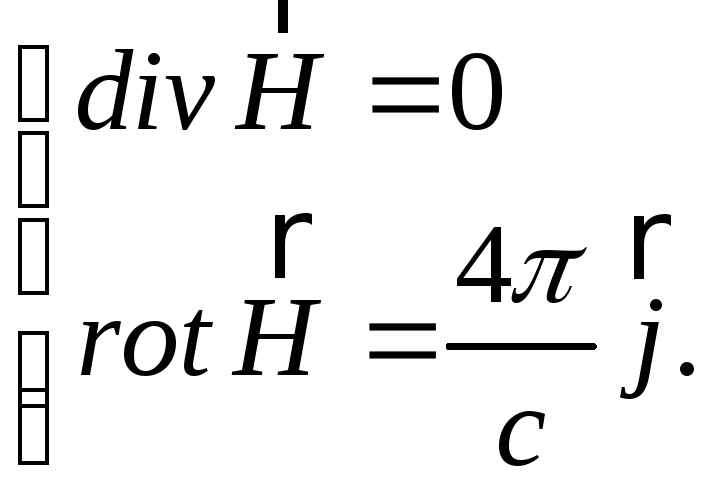(5.7)

Задача. Визначити напруженість магнітного поля, котре утворюється в вакуумі тонким прямолінійним нескінченним провідником, по якому тече ток .

Використаємо метод безпосереднього підсумування. Вибиремо начало відліку в точці (Рис.8),

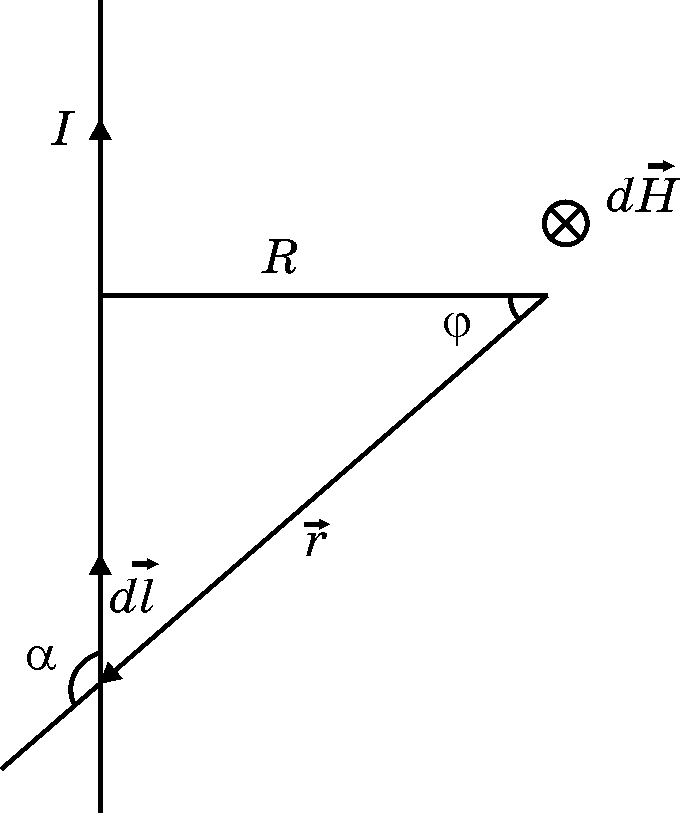
Рис. 8. Магнітне поле тонкого прямолінійного нескінченного провідника.

Тоді:

.

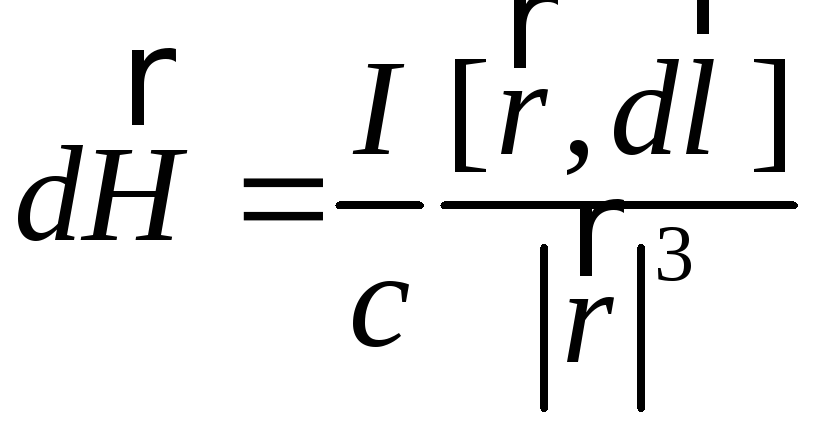Із визначення векторного добутку знаходимо напрямок вектора :

.

Модуль вектора дорівнює:

.

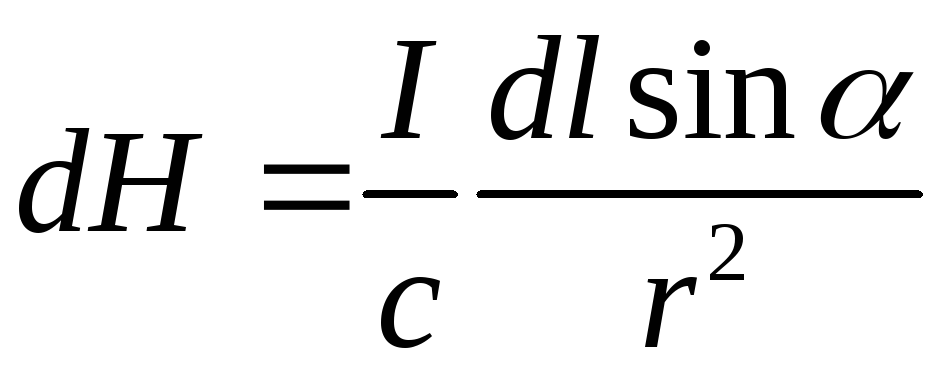Оскільки всі елементи спрямовані однаково, можно твердити, що , при цьому:

.

Використання теореми про циркуляцію вектора напруженості магнітного поля дозволяє швидше одержати розв’язок. Вибираємо контур з радіусом , таким чином, що провідник проходе перпендикулярно до контура через його центр. Тоді:

.

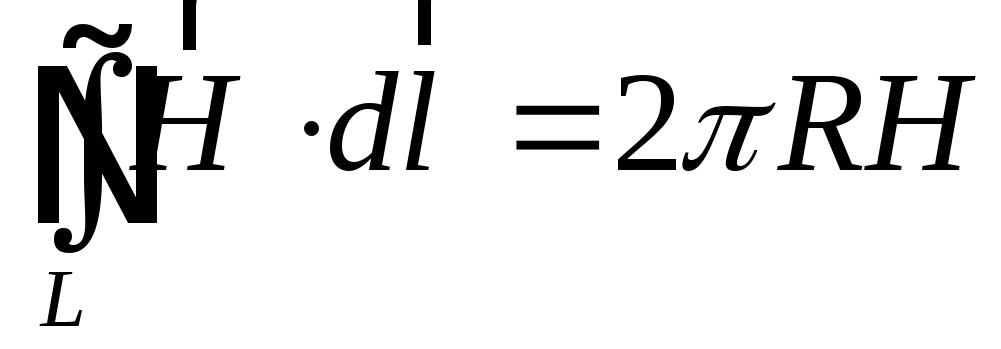З іншого боку:

.

Звідки маємо:

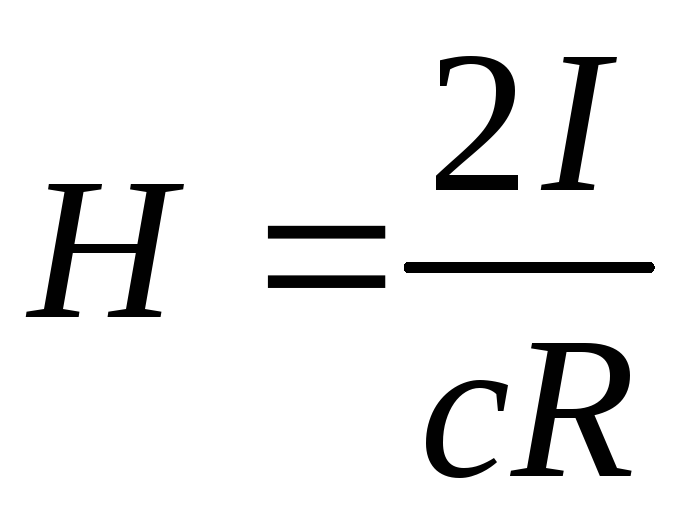. (5.8)

Знайдемо розв’язок за допомогою рівнянь максвелла (4.3), які в даній задачі

приймають вигляд:

.

Згідно з симетрією задачі: . Неважко впевнитись, що перше рівнян-ня задовольняється тотожно. Друге рівняння в циліндричних координатах має вигляд:

.

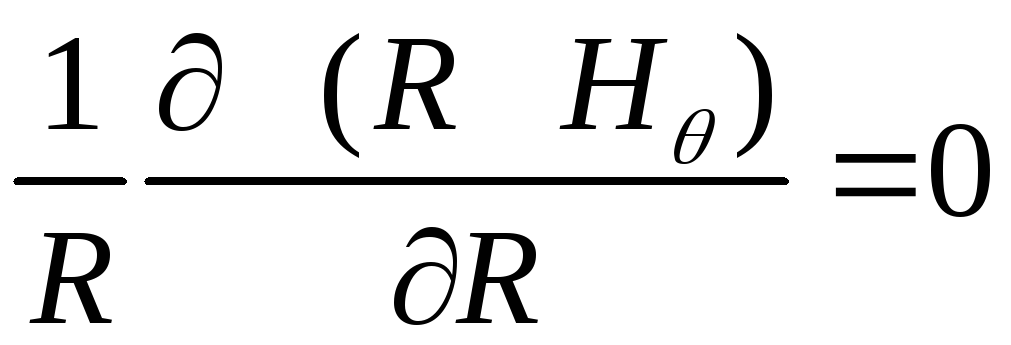Розв’язок:

.

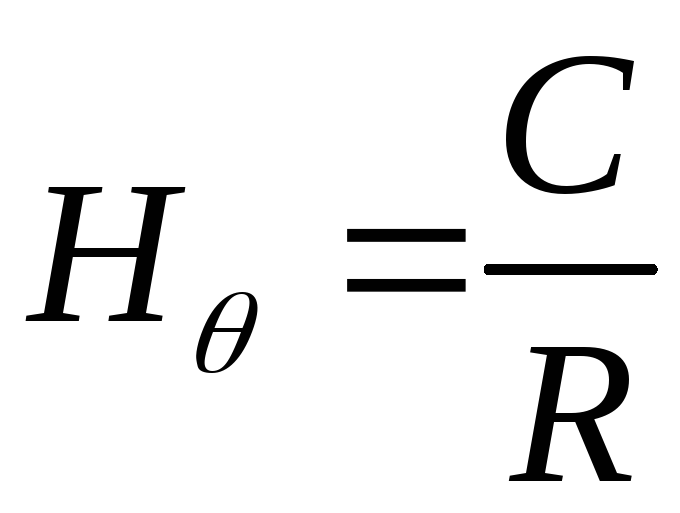Для визначення константи треба було б розглядати лінійний ток як граничний випадок току, який протікає через поперечний переріз циліндричного провідника (див. слідуючу задачу). Таким чином можна знайти:

.

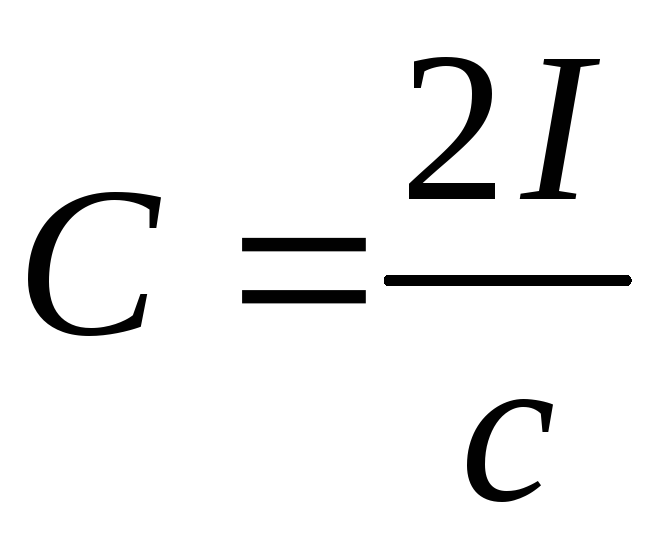Задача. Вдовж циліндричного провідника радіуса тече однорідний ток . Визначити векторий потенціал та напруженість магнітного поля.

Використаємо метод інтегрування рівняння Пуасона. Для внутрішньої області:

.

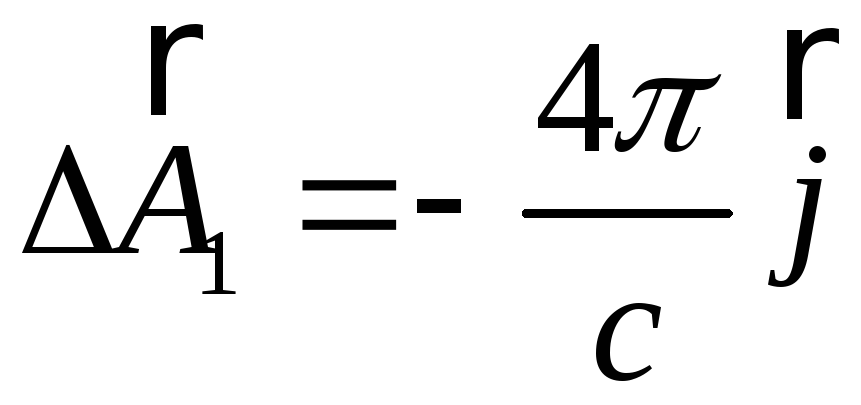Оскільки в циліндричній системі координат , то можна твердити, що . Таким чином:

.

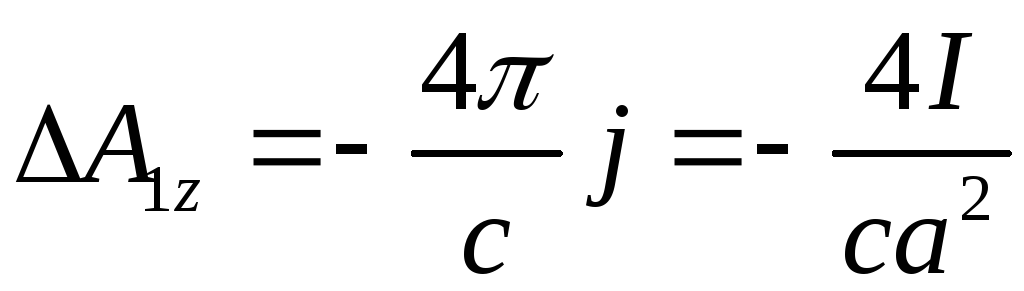Оскільки система має циліндричну симетрію, залежить тільки від . Тоді:

.

Розв’язок цього рівняння:

.

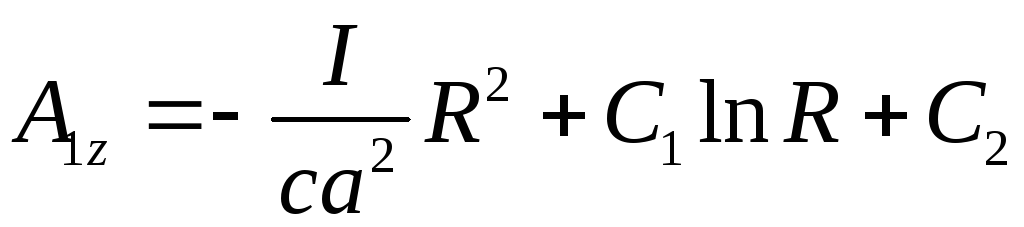Із умови обмеженості поля в точці маємо: . Для зовнішньої області:

.

Розв’язок цього рівняння аналогічний попередньому:

.

Без обмеження загальності можна вважати . Таким чином, маємо розв’язок:

;

.

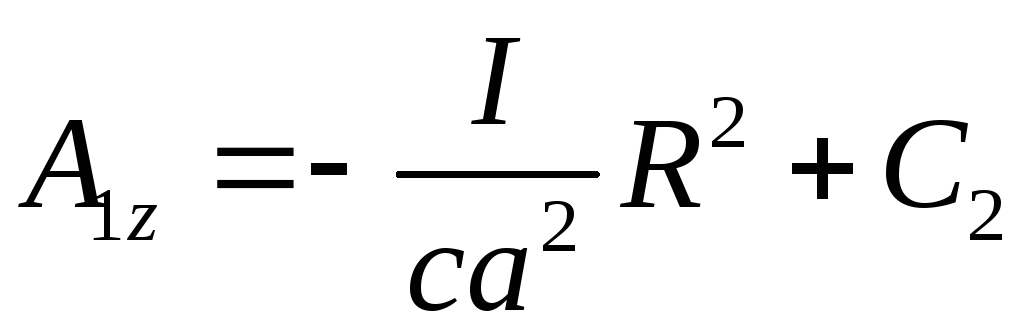Із умови неперервності векторного потенціала знаходимо зв’язок між константами:

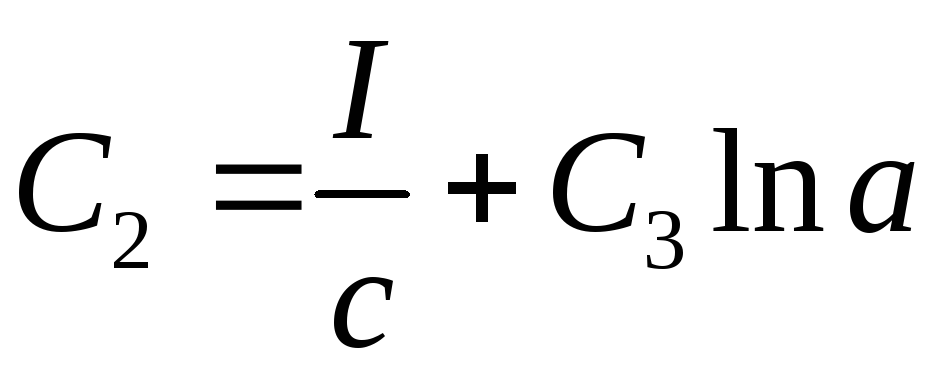. (5.9)

Напруженість магнітного поля знаходимо за формулою (5.2). Тоді маємо:

;

.

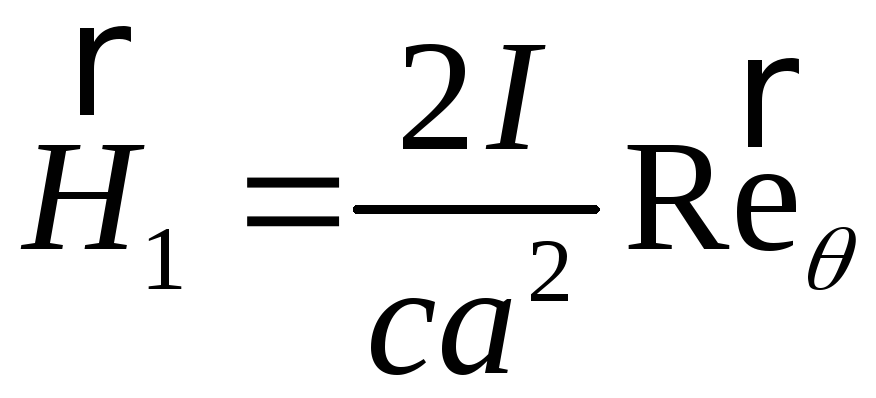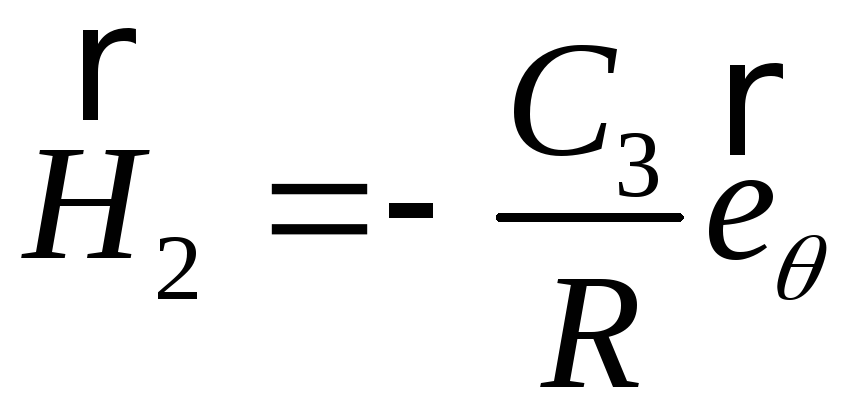Із граничної умови знаходимо константу :

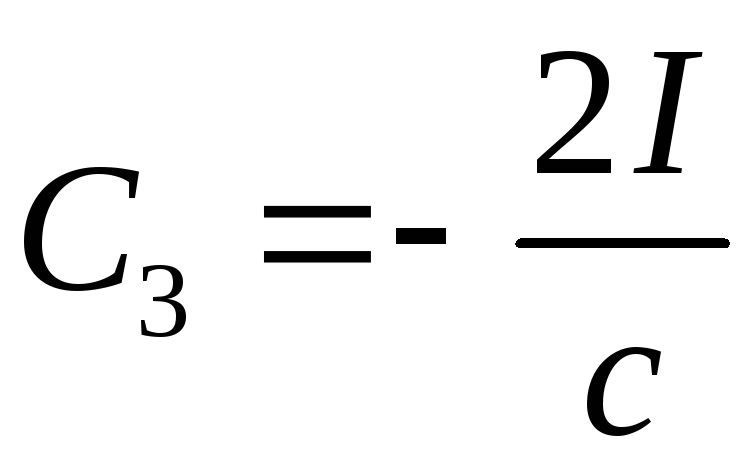. (5.10)

Таким чином

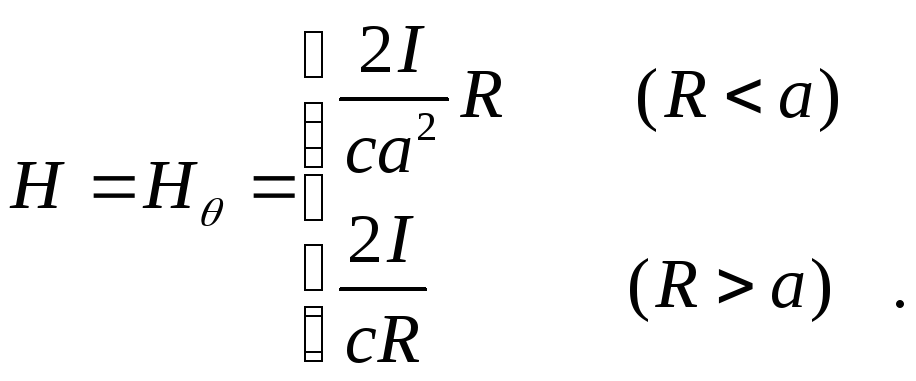
Враховуючи (5.9) і (5.10) знаходимо константу :

.

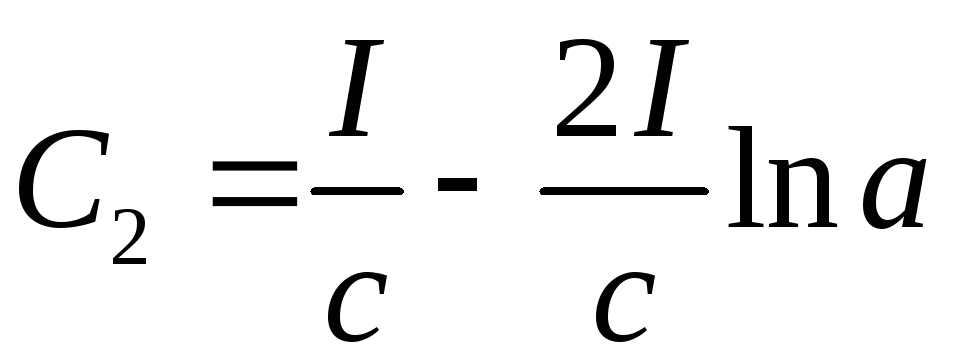Остаточно, векторний потенціал дорівнює:

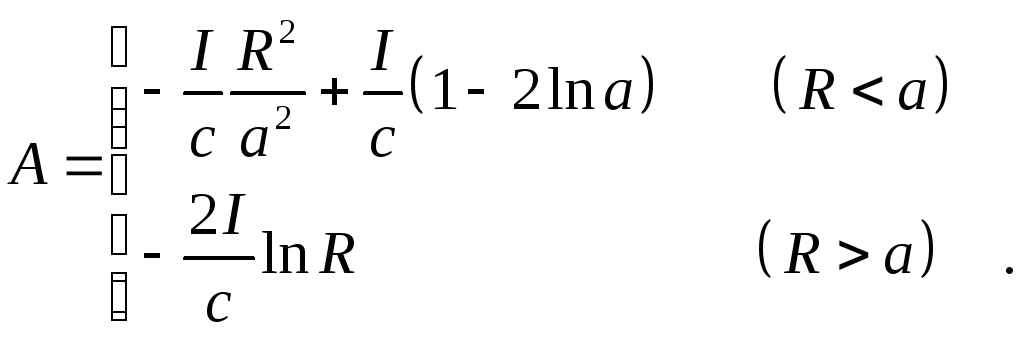(5.11)

Задачі.

1) В циліндричному провіднику радіуса просвердлено круглий канал радіуса , ось якого паралельна до осі циліндра і розташована від неї на відстані . По металевій частині циліндра тече однорідний ток, спрямований вдовж осі. Визначити величину і напрямок магнітного поля.

2) Вдовж нескінченої плоскої полоси, котра має ширину тече ток, який рівномірно розподілений за її шириною з густиною поверхневого тока . Визначити магнітне поле. Розглянути його поведінку на великій відстані від полоси.

3) Знайти векторний потенціал і напруженність магнітного поля, яке утворюється током, що тече по кільцю радіуса . Окремо розглянути випадок, коли точка спостереження знаходиться на великій відстані від кільця.

4) Визначити векторний потенціал і напруженість линійного соленоіда., який має витків на одиницю довжини, а ток дорівнює . Одержати результат:

а) за допомогою підсумування полів окремих витків;

б) за допомогою граничного переходу у формулі для тороїдальної катушки.

5) З якою силою взаємодіють нескінченно довгий циліндричний провідник, по поверхні якого тече ток , і лінійний ток кінцевої довжини. (Вважати, що лінійний провідник, довжиною , є паралельним до осі циліндричного провідника і знаходиться на відстані від неї.

6) Заряд рухається вдовж кола радіуса з лінійною швидкостю . Визначити:

а) гіромагнітнє відношення (відношення магнітного момента до механічного);

б) середнє значення векторного потенціала і напруженості магнітного поля.

7) Знайти силу і обертальний момент , які діють на замкнутий тонкий провідник з током в однородному магнітному полі . Відповідь одержати для довільного контура. Обговорити випадки контурів у вигляді:

а) рамки з током (вісь рамки перпендикулярна до поля);

б) кругового витка.

8) По нескінченно довгому порожньому циліндру тече ток з постійною густиною . Внутрішній та зовнішній радіуси циліндра дорівнюють відповідно і . Вдовж осі циліндра проходить лінійний провідник, по якому тече ток тії ж величини в протилежному напрямку. Визначити параметри магнітного поля.

9) Сфера радіуса обертається з кутовою швидкісьтю навколо одного зі своїх диаметрів. Заряд сфери рівномірно розподілений за її об’ємом. Визначити:

а) магнітний момент сфери;

б) напруженість магнітного поля всередині сфери та поза її межами.

10) За допомогою максвелівського тензора натягів обчислити силу взаємодії у повітрі між двома паралельними нескінченними прямолінійними токами. Сили токів і , відстань між ними .

5.2 Мультипольний розклад в магнітостатиці

Подібно до того, як в електростатиці скалярний потенціал розкладається в ряд за мультиполями, в магнітостатиці можна розкласти в ряд векторний потенціал . Оскільки магнітні заряди не існують, перший член такого розкладу завжди дорівньює нулеві. Перший, відмінний від нуля, внесок дорівнює:

, (5.12)

де -магнітний момент системи.

Він визначається за формулою:

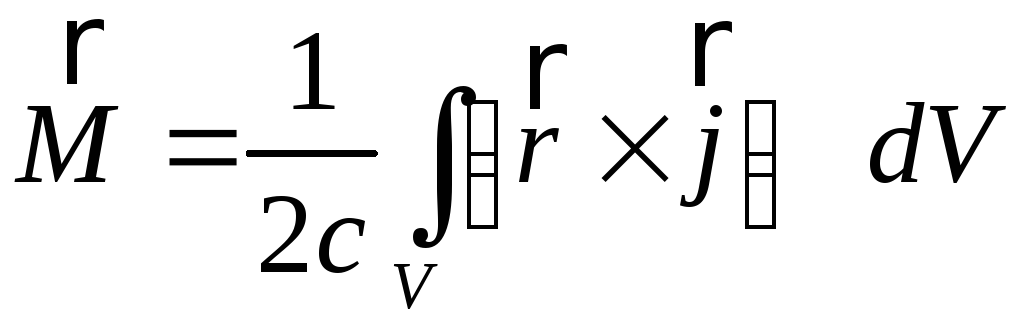. (5.13)

Задача. Знайти векторний потенціал магнітного поля, яке утворюється круговим током з радіусом кола .

Формула (74) для лінійного тока повина бути переписаною у вигляді:

,

де -одиничний вектор, дотичний до кола у точці, яка задається радіус-вектором .

Неважко бачити, що

,

де -одиничний вектор, перпендикулярний до круга. Завдяки цьому

.

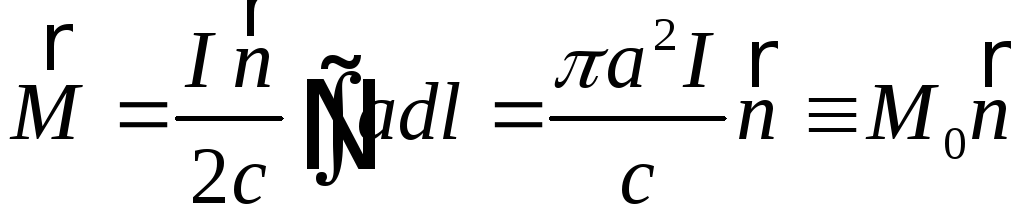Векторний потенціал у магнітодіпольному наближенні, згідно з (73), дорівнює:

.

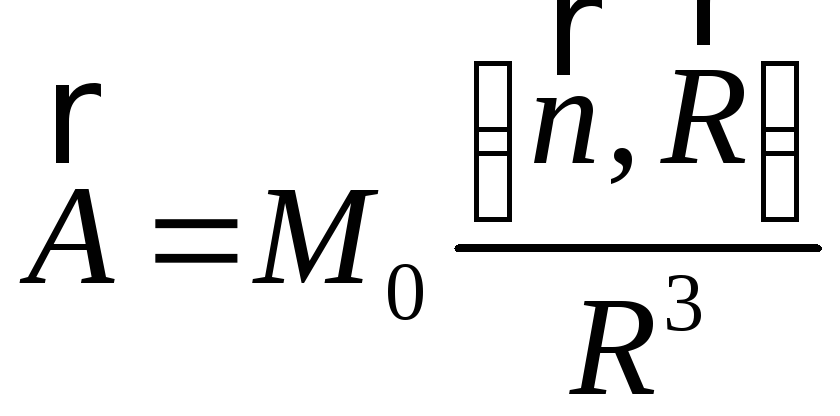У циліндричних координатах з віссю , направленою вдовж , вектор має компоненти:

.

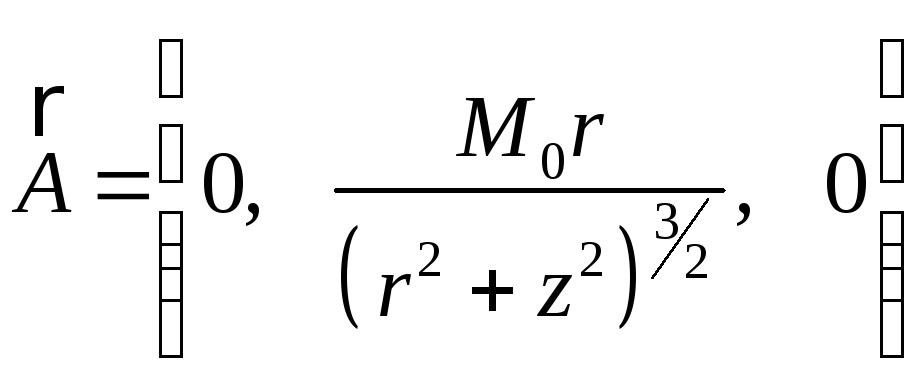Задача для самостійного розв’язування.

Сфера радіуса повертається навколо свого діаметра з кутовою швидкістю навколо одного зі своїх діаметрів. Заряд сфери рівномірно розподілен за об’ємом. Визначити магнітний момент сфери.