Для студентов / Методички / (1)Методичка - ВЕД / ЧI_Р3

РОЗДІЛ 3. ДИФЕРЕНЦІЙНІ ОПЕРАЦІЇ: ГРАДІЄНТ, ДИВЕРГЕНЦІЯ, РОТОР

3.1 Похідна за напрямком та градієнт

Нехай задано скалярне поле , де - довільна точка простору. Проведемо через точку пряму в напряку та виберемо на ній іншу точку .

Похідною скалярного поля за напряком в точці називається ліміт:

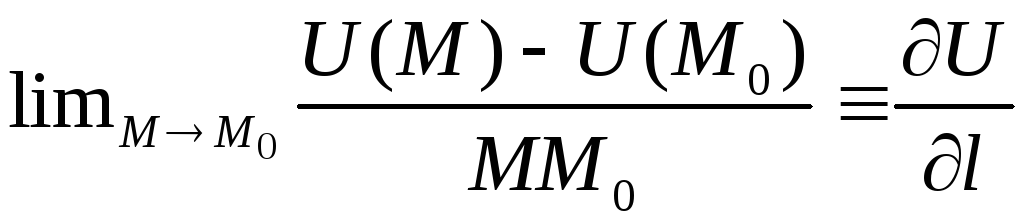(3.1)

Через будь-яку точку можна провести нескінчену множину прямих, тому в кожній точці існує нескінчено багато похідних за напрямком.

Градієнтом скалярного поля в точці називається вектор , який задовольняє таким умовам:

а) він за напрямком співпадає з напрямком найшвидшого зростання функції ;

б) його модуль дорівнює швидкості зростання функції в цьому напрямку.

В довільних ортогональних координатах:

. (3.2)

Приклад: Обчислити градієнт функції .

Оскільки функція залежить лише від модуля радіус-вектора, доцільно користуватись сферичними координатами. В них:

.

Нехай задано стаціонарне (яке не залежить від часу) векторне поле . Якщо існує така скалярна функція , що для кожної точки поля виконується умова:, то поле називається потенційним, а функція - скалярним потенціалом векторного поля .

Електростатичне поле є потенційним полем. Зв’язок напруженості поля зі скалярним потенціалом дається формулою:

. (3.3)

Вектор в кожній точці поля перпендикулярний до поверхні , тому силові лінії електростатичного поля перпендикулярні до поверхнєй рівня (Рис.7).

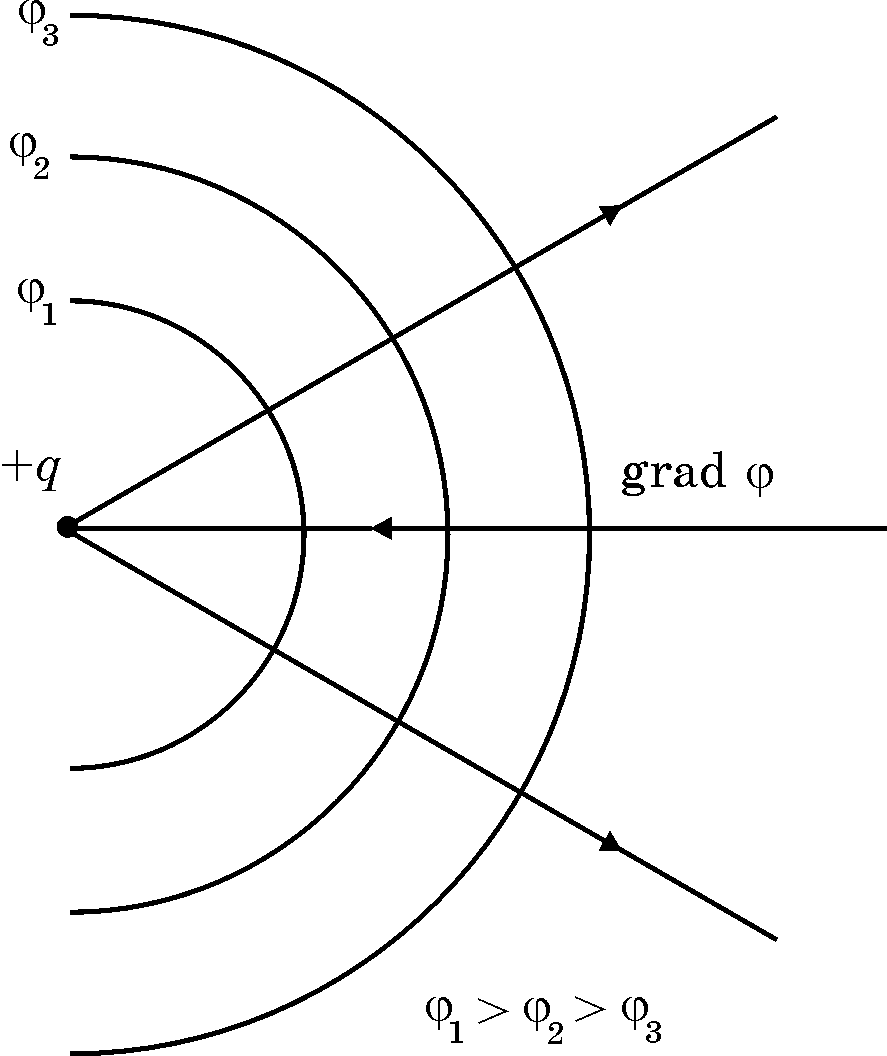
Рис. 7. Силові лінії електростатичного поля та поверхні рівня.

Задача. Потенціал поля, яке утворюється точковим зарядом , дається формулою: 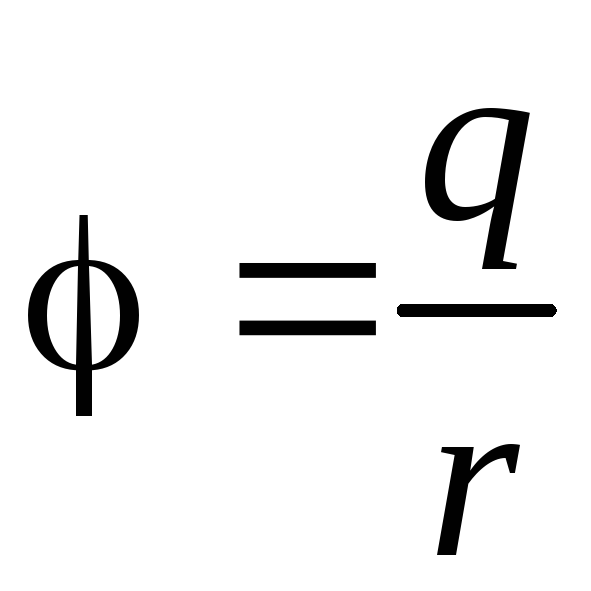. Знайти напруженість поля.

Напруженість поля знаходимо за формулою:

.

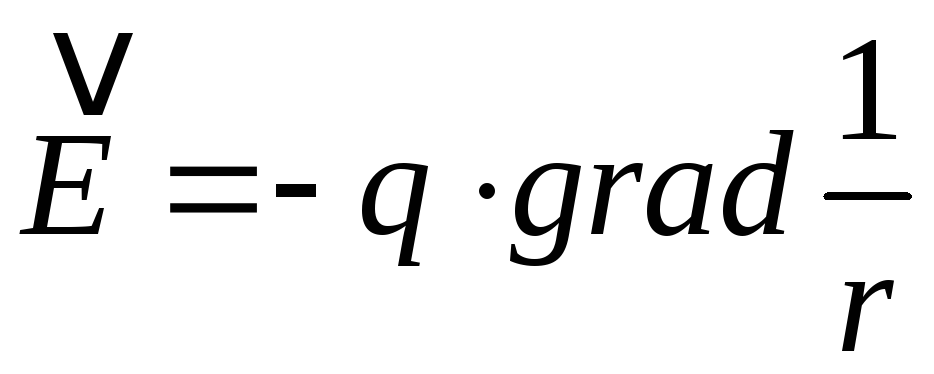В сферичних координатах:

,

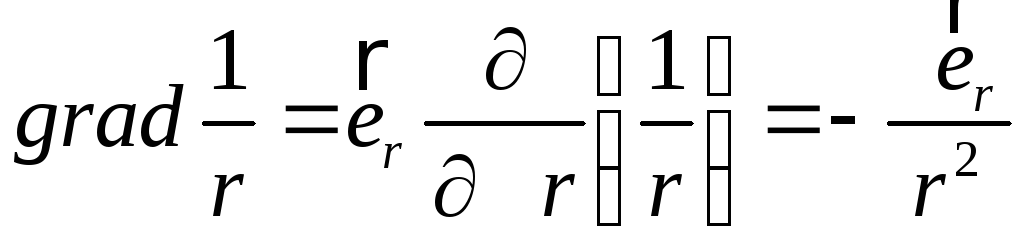тоді:

.

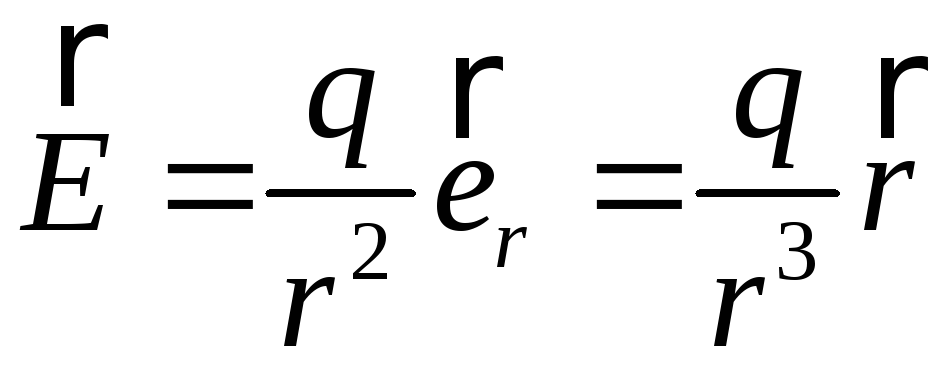Поверхні рівня є сферами, а силові лінії спрямовані вдовж радіус-векторів.

Циркуляція вектора потенційного поля вдовж будь-якого замкнутого контура дорівнює нулеві. Оскільки електростатичне поле є потенційним, можна твердити:

, (3.4)

де - будь-який замкнутий контур.

3.2 Дивергенція в довільних криволінійних ортогональних координатах

Нехай задано векторне поле . Побудуємо навколо точки поверхню , яка охоплює об’єм . Дивергенцією векторного поля в точці називається границя:

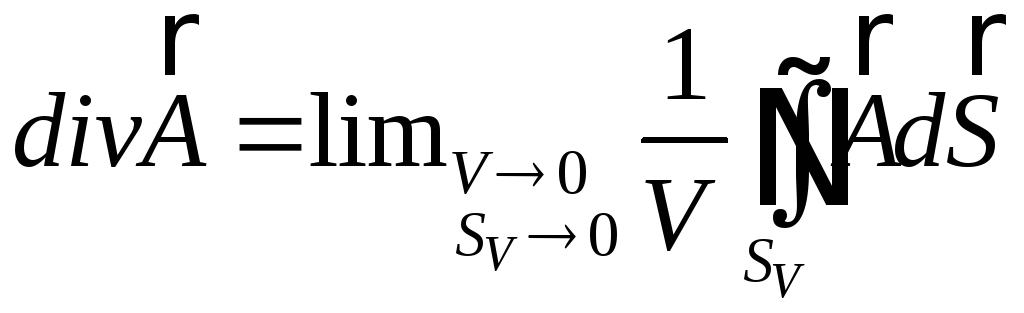. (3.5)

Виберемо як поверхню криволінійного паралеліпипеда, яка утворена координатними поверхнями. Тоді

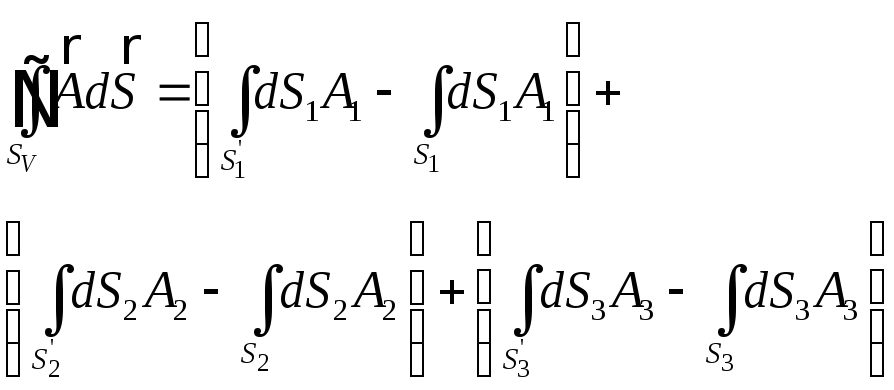(3.6)

Тут , , -поверхні, які проходять через початок координат, а , , -поверхні, які зсунуті з початку координат на , , .

Розглянемо детальніше різницю інтегралів у першій скобці. Оскільки , то

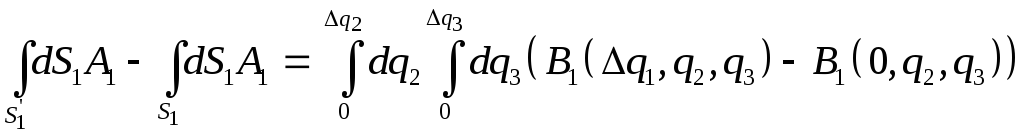, (3.7)

де .

Тепер використаємо тотожність

.

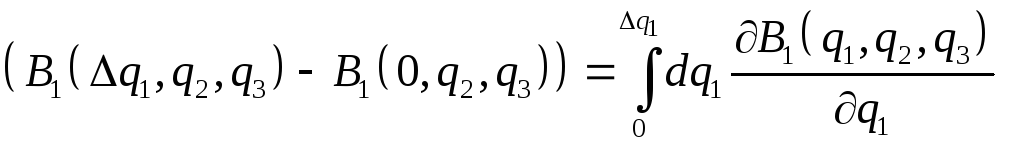Враховуючи також, що , формулу (3.7) можна переписати у вигляді

.

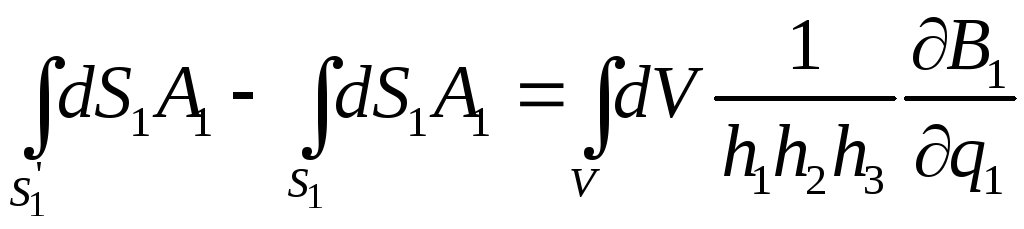Аналогічно можна перетворити і дві інші різниці інтегралів у (3.6). Тому

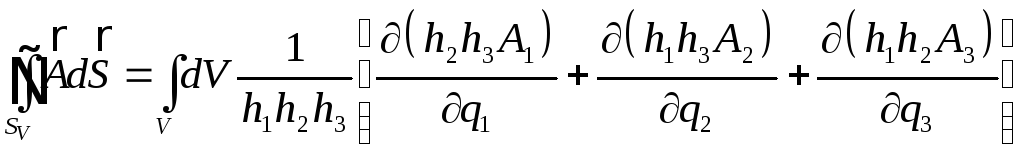
Скориставшись теоремою про середнє

,

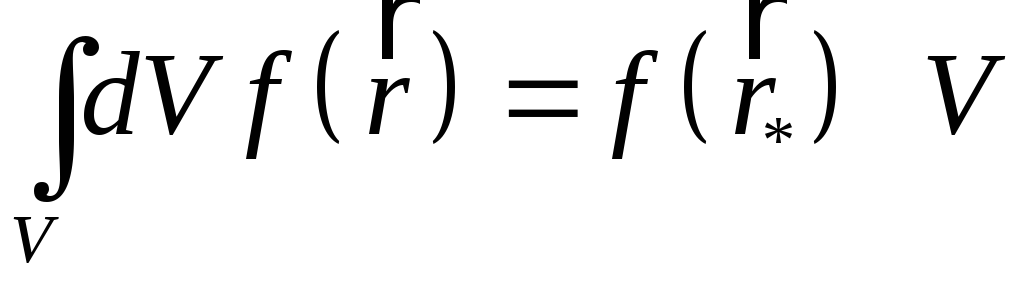де , знаходимо:

. (3.8)

З (3.5) та (3.8) витікає, що дивергенція довільного поля у криволінійних ортогональних координатах дорівнює:

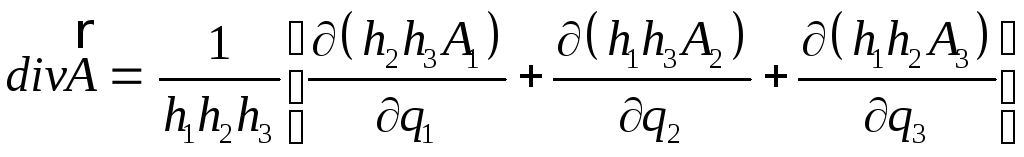. (3.9)

Приклад: обчислити дивергенцію радіус-вектора.

В декартових координатах:

,

тому

.

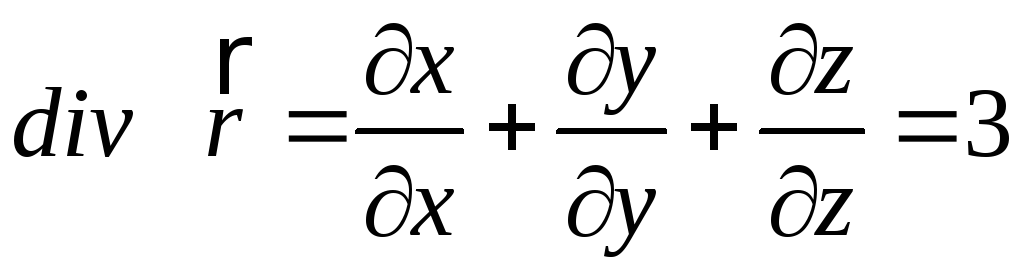Приклад. Обчислити .

В сферичних координатах:

,

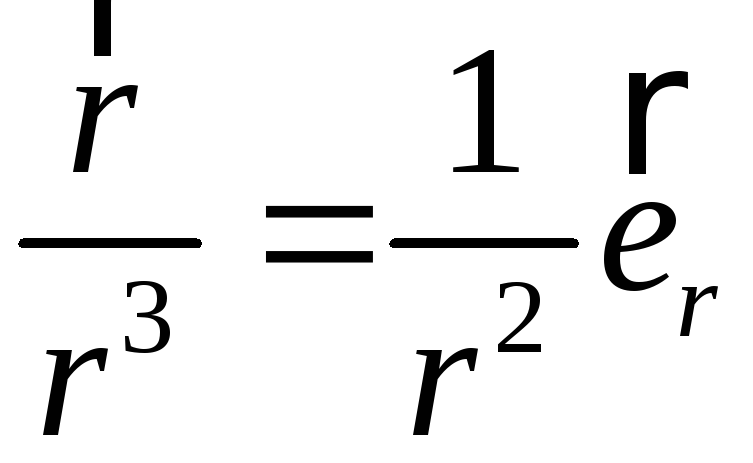тому

.

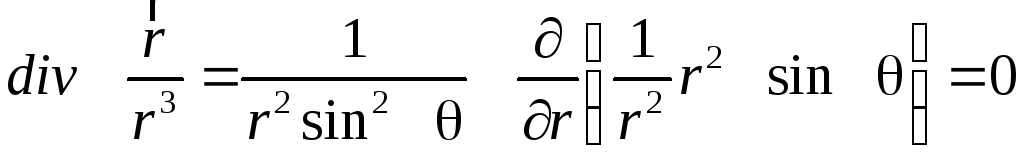3.3 Ротор в довільних криволінійних ортогональних координатах

За визначенням, проекція вектора на довільний напрямок , задається виразом:

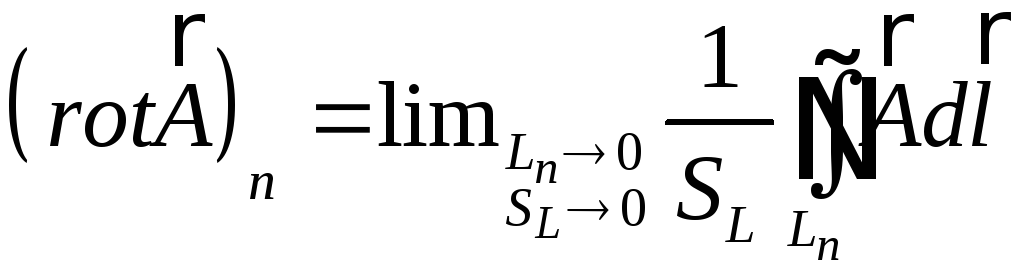, (3.10)

де - контур, який належить поверхні, що перпендикулярна до вектора , ‑ площа поверхні, яку охоплює контур .

Нехай вектор направлений вдовж базисного вектора , а контур має форму криволінійного паралелограма, утвореного координатними лініями і . В цьому випадку:

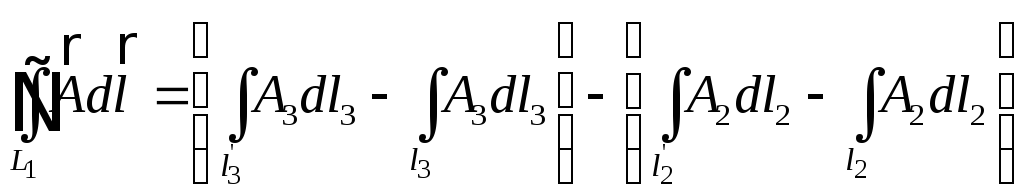, (3.11)

де і -сторони паралелограма, які проходять через початок координат, а і - сторони паралелограма, які зміщени на та відповідно.

Неважко бачити, що

,

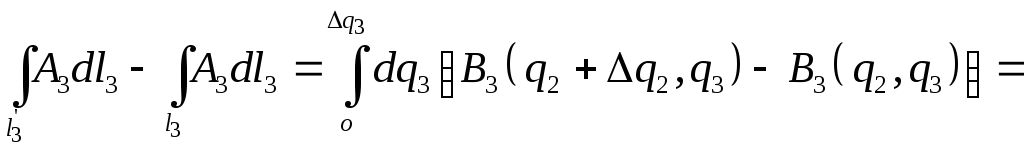
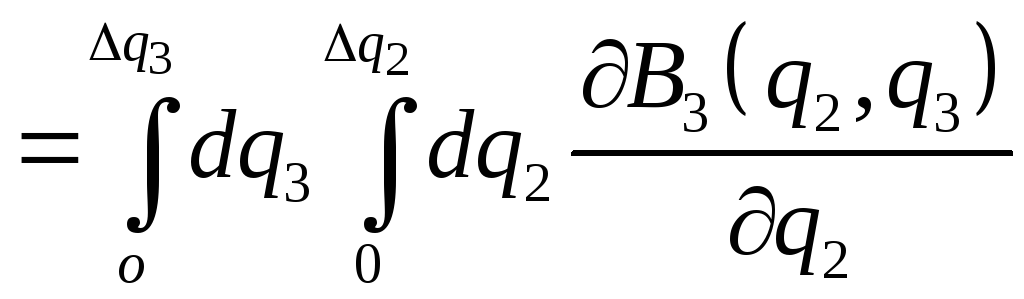де .

Друга різниця інтегралів у (3.11) перетворюється аналогічно. Враховуючи, що

,

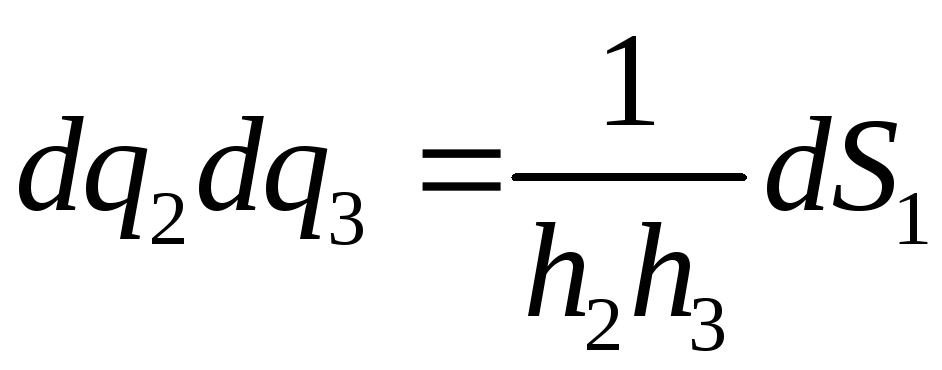циркуляцію вектора по контуру можна представити у вигляді

.

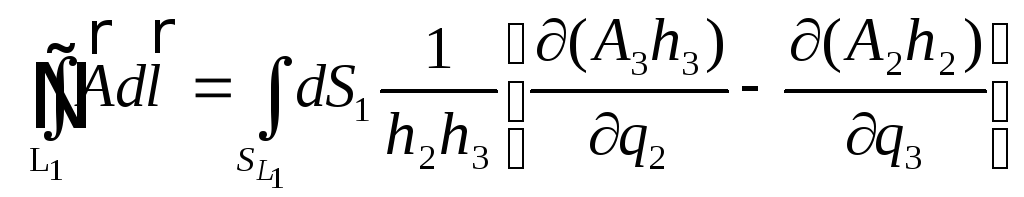За допомогою теореми про середне:

,

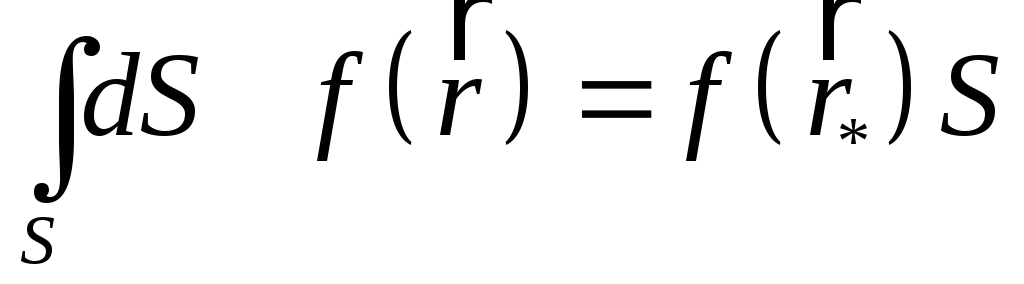ми знаходимо

. (3.12)

З (3.10) та (3.12) витікає, що

. (3.13)

Таким чином можна побудувати і дві інші компоненти вектора .

Остаточний результат можна представити у вигляді детермінанту:

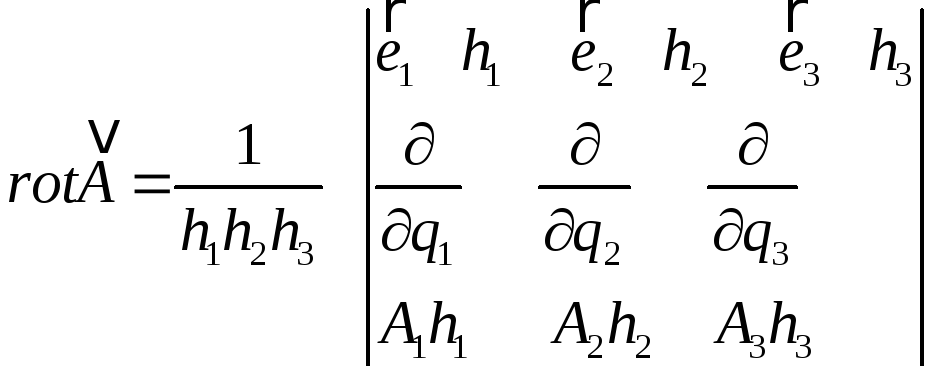. (3.14)

Неважко бачити, що розклад детермінанта за елементами першої строки якраз і приводить до проекцій на базисні орти, подібних до (3.13).

Приклади:

1) обчислити :

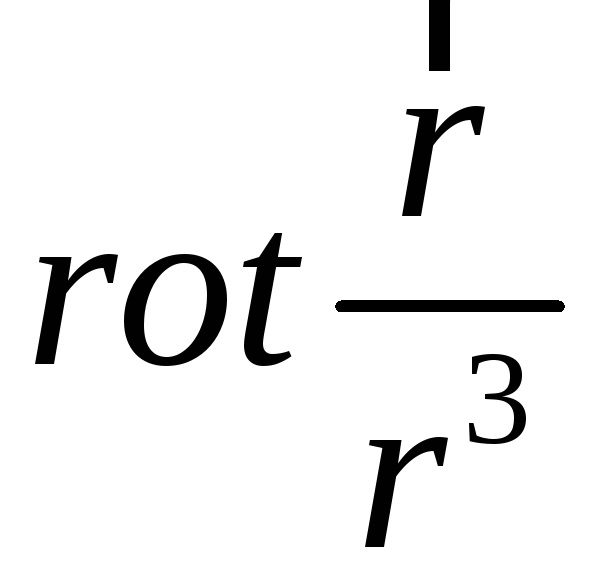а) відповідь 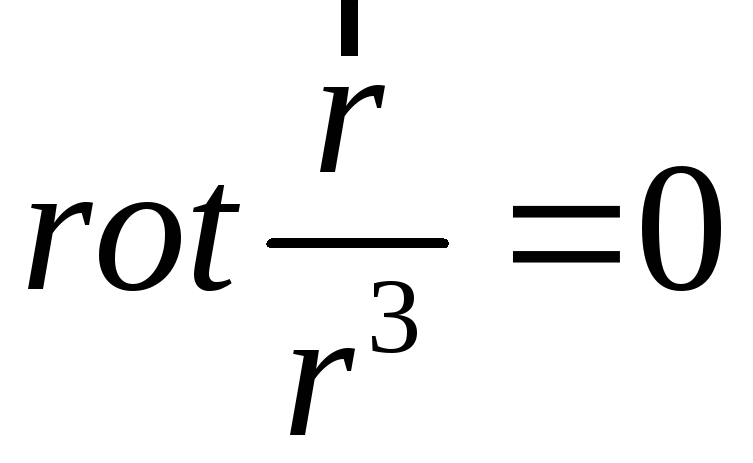можна написати зразу, якщо врахувати, що лініями поля є радіуси-вектори, які в принципі не можуть утворювати вихрьових структур.

б) при формальному підході враховуємо, що вектор має такі сферичні координати: 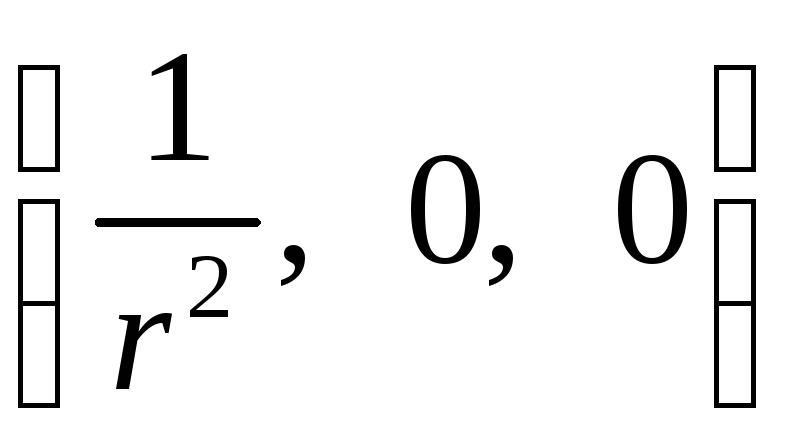. При підстановці їх у (3.14) знаходимо, що .

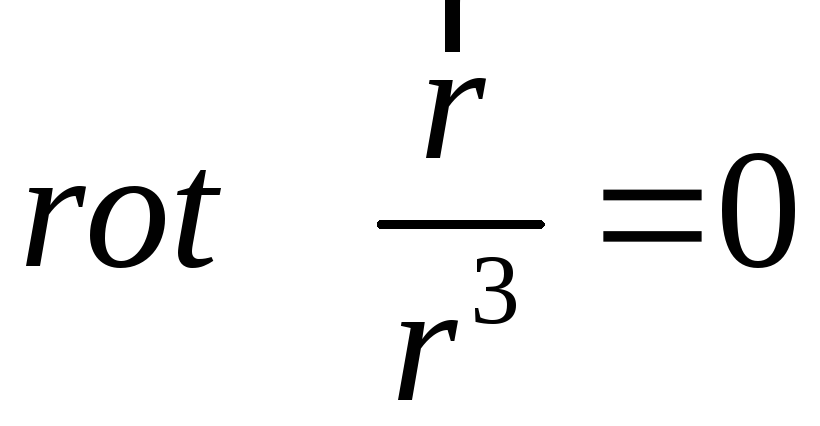2) обчислити .

Вибираємо сферичну систему координат таким чином, щоб полярна вісь збігалась з вектором . Тоді . Згідно з (3.14)

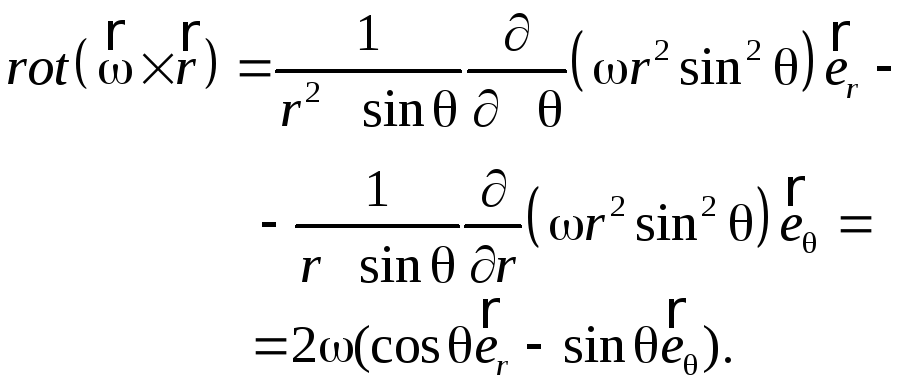
Оскільки , де -орт в напрямку полярної осі (), остаточно маэмо:

.

3.4 Операторний метод

Введемо векторний диференційний оператор:

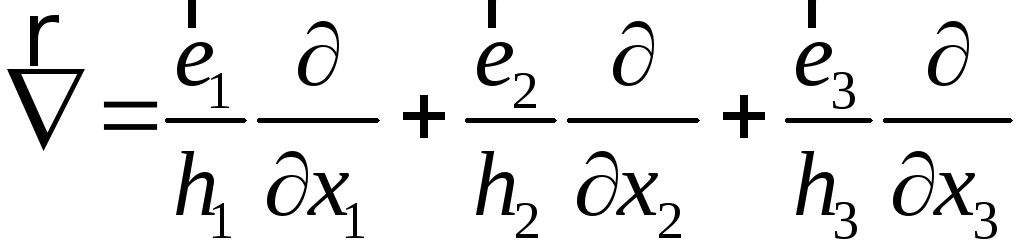, (3.15)

який називається оператором набла.

За допомогою оператора набла основні диференційні операції записуються у такому вигляді

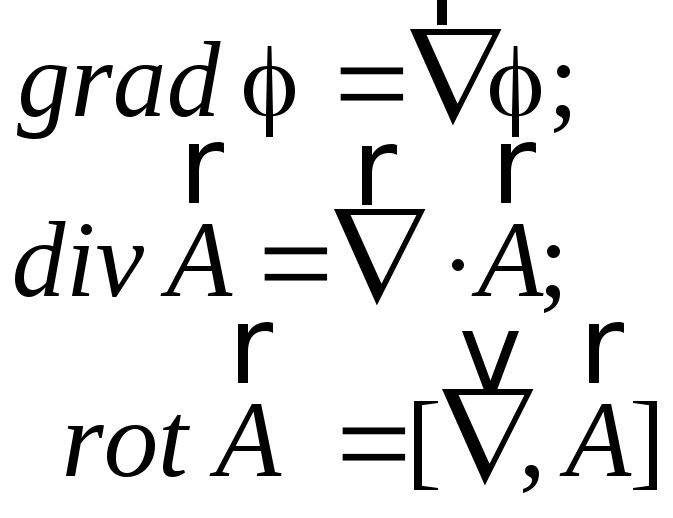. (3.16)

Дифференцюючий комплекс можна записати у такому вигляді:

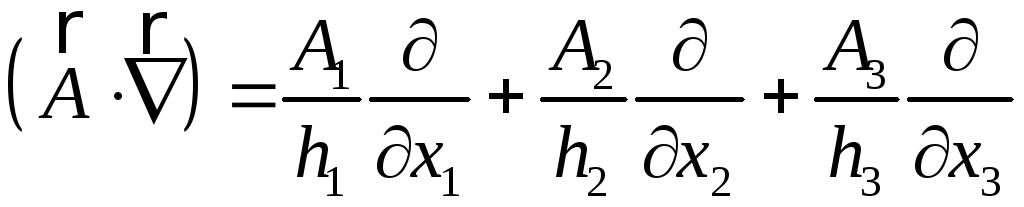. (3.17)

Оператор називають оператором Лапласа, або лапласіаном (дельта).

В довільних ортогональних координатах:

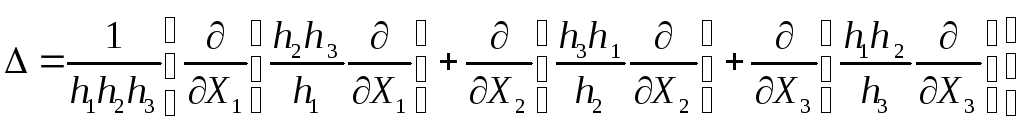(3.18)

Задача. Спростити вирази: , де і - векторні поля.

Завжди слід пам’ятати правило, що вектор-оператор набла діє тільки на функції, які стоять праворуч від нього. Тому байдуже: - постійний вектор або залежить від координат. Спростити вираз – це означає перетворити його так, щоб оператор діяв тільки на один вектор, тобто праворуч від стояв один вектор.

Лінійний оператор має дві властивості:

1. - оператор диференційний. Його дія на складну функцію визначається

правилами диференцювання:

, (3.19)

де - діє тільки на .

2. - вектор. Правила перестановки вектора з іншими векторами повині визначатися правилами векторної алгебри.

Дифференцюючі комплекси і є скалярами, тому правила

перестановки комплексів і векторів і повині бути такі, як у скаляра і векторів:

,

,

Підставляючи ці вирази в (3.19), одержуємо:

.

Задачі для самостійного розв'язку.

1) Спростити вирази: ; ; ;; ;

;;.

2) Обчислити: ; ; ; ; ; ; ; ; ; ,

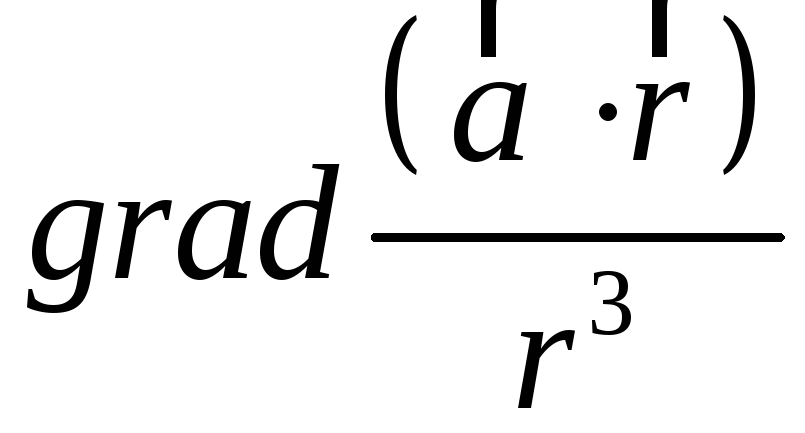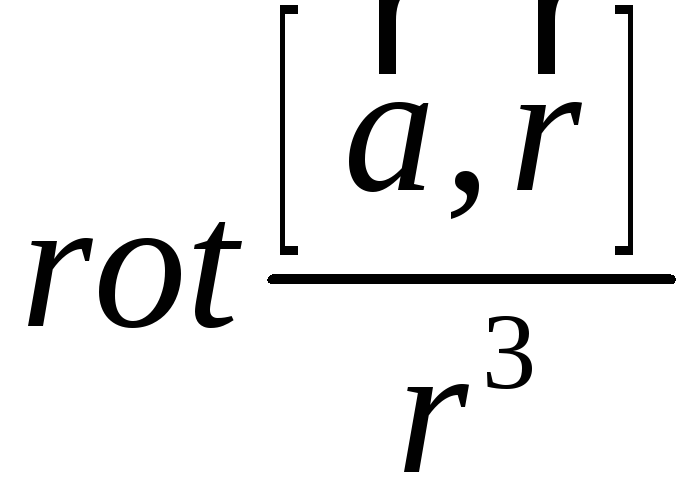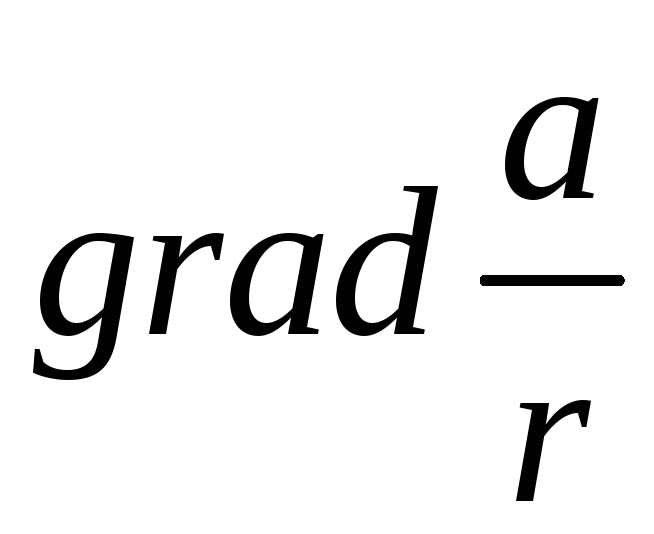де - постійний вектор, - його абсолютне значення.

Часто буває доцільним використання теореми Остроградського-Гауса:

,

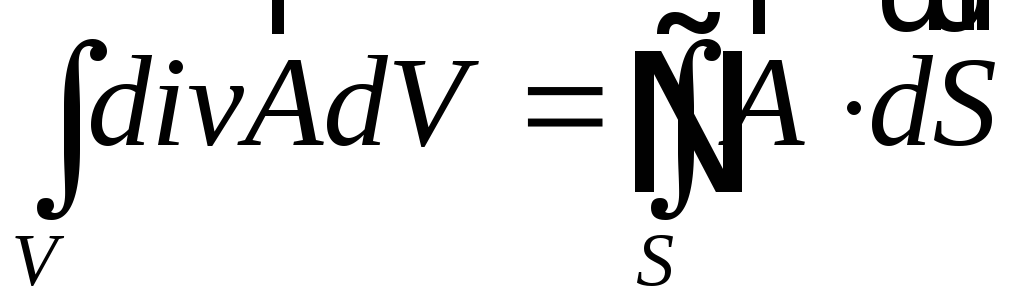де - поверхня, яка охоплює об’єм .

Задача. Використовуючи теорему Остроградського-Гауса довести тотожність:

.

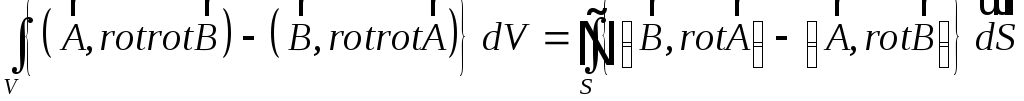Задача. Довести, що .

Ця формула віддалено нагадує формулу Гауса-Остроградського: 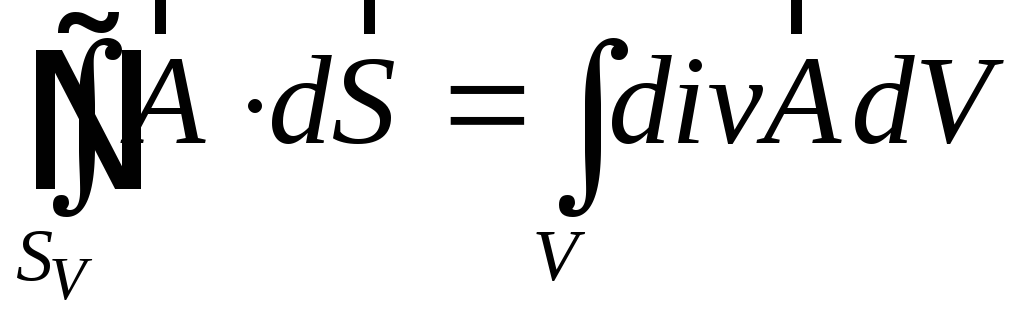. Але вона точно зводиться до неї після домноження лівої частини на постійний вектор . Тоді, згідно з теоремою Гауса-Остроградського:

.

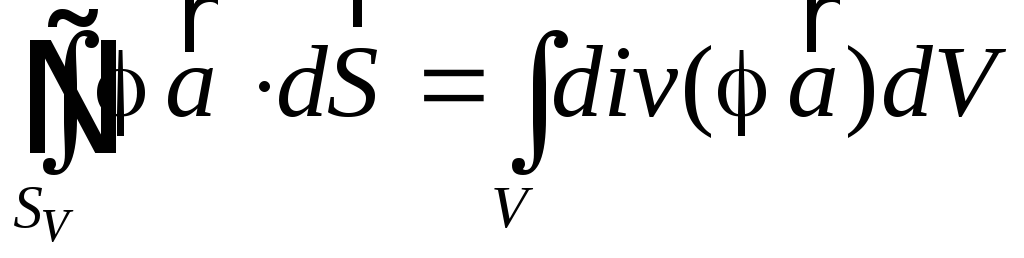Оскільки , то

.

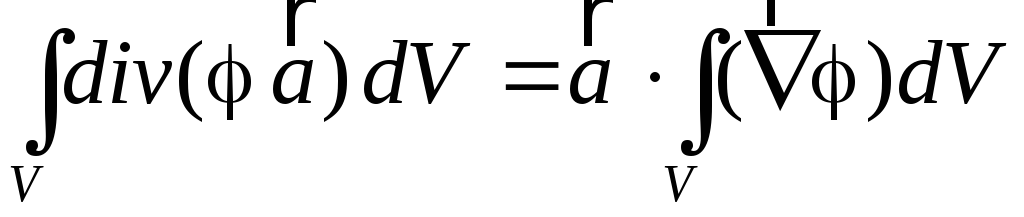Таким чином, ми маємо рівняння

,

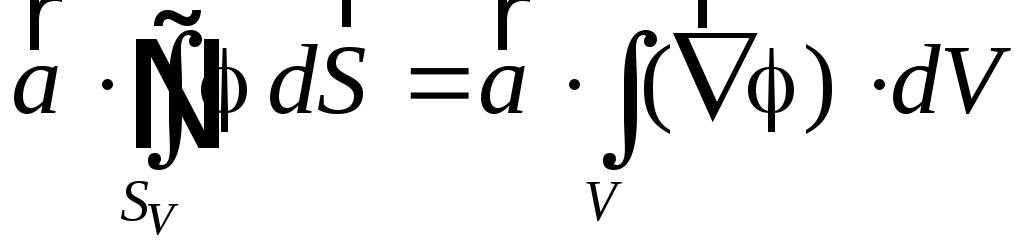яке виконується при довільному . А це і доводить вихідне рівняння.

Задача. Інтеграл , взятий по довільному замкнутому контуру, перетворити в інтеграл по поверхні, яка спирається на цей контур.

Нехай буде ортом, дотичним до контура у його довільній точці . Тоді

,

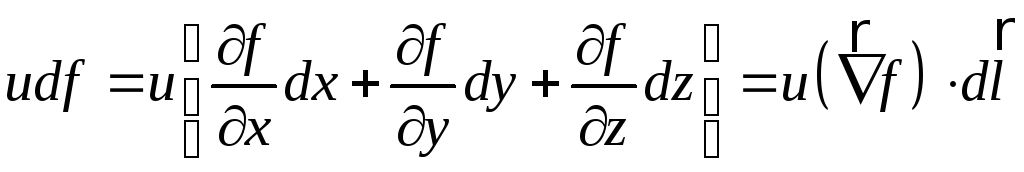де .

Тоді інтеграл за теоремою Стокса перетворюється наступним чином:

.

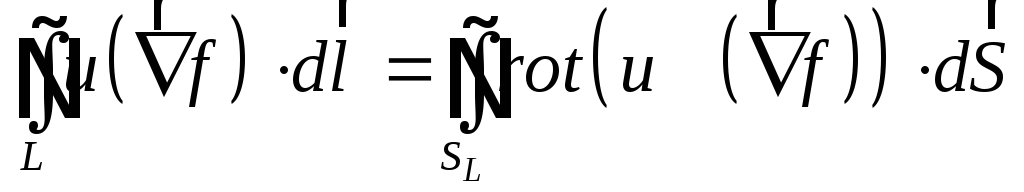Значення неважко отримати за допомогою рівняння:

так, як . У такий спосіб ми отримуємо:

.
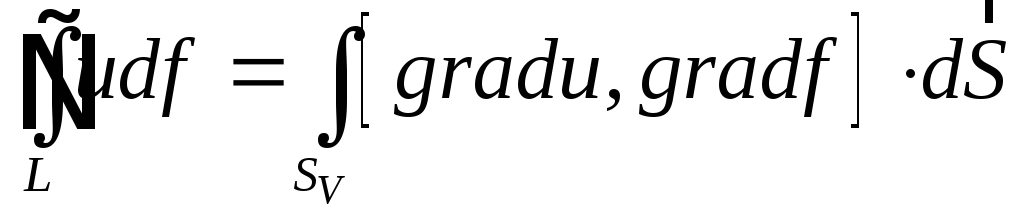