Для студентов / Методички / (3)Методичка - ЕСС / (3)Ємності конденсаторів

Ємності конденсаторів

Задача 1. Знайти ємність сферичного конденсатора, радіуси обкладинок якого дорівнюють і , , а діелектрична проникненість між обкладинками змінюється за законом . Розглянути окремі випадки: а), б) і в) .

Розв’язок:

За означенням, ємність конденсатора визначається співвідношенням:

, (1)

де і - заряди зовнішньої і внутрішньої обкладинок конденсатора, а - різниця потенціалів між ними. Таким чином, для розв’язку треба встановити зв'язок між і .

З умови задачі випливає, що електричне поле всередині конденсатора є радіально симетричним: , а . Різниця потенціалів між обкладинками і напруженість поля між ними пов’язані рівнянням:

. (2)

Для знаходження напруженості електричного поля скористаємось рівняннями електростатики:

(3)

і граничними умовами:

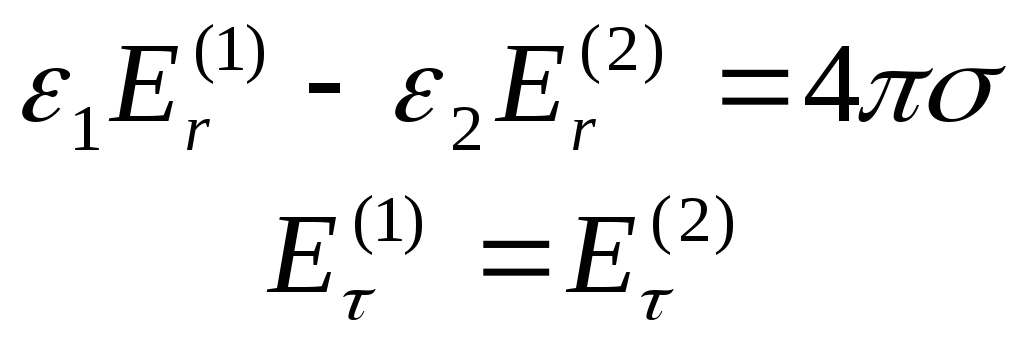, (4)

де - поверхнева густина заряду на внутрішній обкладинці конденсатора. Оскільки електричне поле є радіально симетричним, то другі рівняння в (3) і (4) задовольняються тотожньо. Перше з рівнянь (3) приймає вигляд:

і призводить до розв’язку:

. (5)

Враховуючи, що зовні конденсатора електричне поле відсутнє, тобто , з першого рівняння (4) знаходимо:

. (6)

Комбінуючи (2), (5) і (6), знаходимо:

. (7)

Остаточно, з (1) і (7) випливає, що ємність сферичного конденсатора, заповненого діелектриком з проникненістю , дорівнює:

. (8)

а) В найпростішому випадку, коли ,

. (9)

Ємність плоского конденсатора. Розглянемо тепер граничний випадок, коли , але так, що . Локально сферичний конденсатор перетворюється в плоский. Очевидно, що

,

де

(10)

- ємність плоского конденсатора з розрахунку на одиницю площі. Якщо пластини плоского конденсатора мають площу , то його ємність дорівнюватиме:

. (11)

б) В другому випадку

,

так що

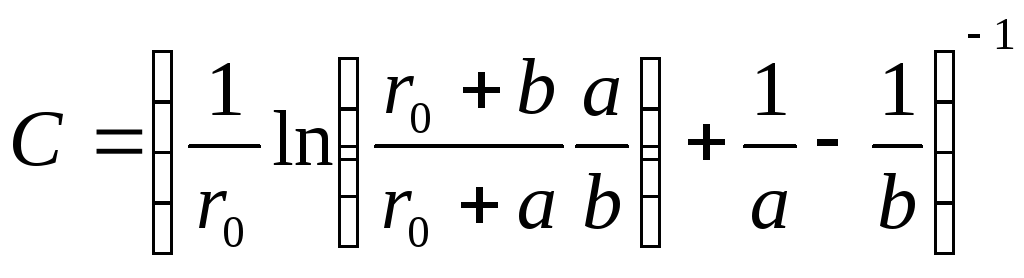, (12)

де є характерна відстань, на якій змінюється діелектрична проникненість прокладки конденсатора. Якщо , результат (12) переходить в (9). В протилежному випадку, коли , формула (12) з точністю апроксимується виразом:

. (13)

Зауваження 1: Діелектрична проникненість речовини повинна задовольняти нерівності: . Перша нерівність відображає той факт, що діелектрична проникненість речовини не може бути меншою від діелектричної проникненості вакуума, яка приймається за одиницю. Друга нерівність пов’язана з тим, що переважна більшість діелектриків має проникненість, меншу за діелектричну проникненість води. Тому, вираз є коректним тільки тоді, коли , а товщина діелектричної прокладки є меншою від .

в) В третьому випадку

, (14)

де .

Зауваження 2: Тут також повинна задовольнятись нерівність: або у більш зручному вигляді: .

Задача 2. Знайти ємність плоского конденсатора в присутності провідної сфери, відстань до якої набагато перевищує радіус сфери і розміри конденсатора. Площа пластин конденсатора, відстань між ними і діелектрична проникненість прокладки дорівнюють відповідно , і .

Розв’язок:

З фізичної точки зору сфера буде впливати на конденсатор наступним чином:

1) На далеких відстанях від плоского конденсатора його поле буде полем диполя, утвореного зарядами обкладинок;

2) Поле конденсатора диполя поляризує провідну сферу і вона набуває дипольного моменту;

3) В свою чергу поле поляризованої сфери буде змінювати значення різниці потенціалів між обкладинками конденсатора.

Як наслідок, ємність плоского конденсатора в присутності провідної сфери буде змінюватись. Для розв’язку поставленої задачі треба розглянути наступні допоміжні задачі:

а) Різницю потенціалів між обкладинками плоского конденсатора в однорідному зовнішньому полі напруженості ;

б) Дипольний момент, який індукується на провідній сфері зовнішнім однорідним електричним полем;

в) Ємність плоского конденсатора в присутності провідної сфери.

а) Для простоти, розглянемо спочатку випадок, коли є перпендикулярним до пластин плоского конденсатора, на яких заряди є відсутніми. Розглянемо поведінку потенціалу електричного поля вдалині від кінців конденсатора. В цьому випадку значення потенціалу будуть залежати тільки від однієї координати: . Нехай одна з пластин конденсатора знаходиться в точці , а друга - в точці . Розв’язки рівнянь Лапласа в областях: 1) , 2) і 3) , очевидно, будуть мати вигляд:

,

,

.

Константи повинні задовольняти умовам 1) неперервності потенціалів на пластинах конденсаторів і 2) неперервності нормальних похідних від потенціалів, оскільки поверхневі заряди на пластинах конденсатора є відсутніми. З другої умови випливає:

і

.

Таким чином,

,

,

.

Одну з констант, а саме , можна покласти рівною нулю, що випливає з умови неоднозначності вибору потенціалу. Тоді з неперервності потенціалу випливає, що . Зрозуміло, що константа , тобто

,

,

.

З усього цього робимо висновок, що внесення незарядженого плоского конденсатору в зовнішнє поле, напруженість якого є перпендикулярною до пластин конденсатора, не порушує неперервність потенціалу і напруженості електричного поля. Разом з тим, різниця потенціалу між обкладинкою, яка розташована в точці і має позитивний заряд з її внутрішнього боку, і другою дорівнює:

. (15)

б) Якщо вектор напруженості зовнішнього поля буде направленою під деяким кутом до обкладинок конденсатора, то можна представити у вигляді:

,

де - одиничний вектор, перпендикулярний до обкладинок конденсатора. Зрозуміло, що поздовжня складова напруженості поля приведе до перерозподілу зарядів на пластині, внаслідок чого силові лінії поля стануть перпендикулярними до обкладинок. Але різниця потенціалів між пластинами буде обумовленою тільки нормальною складовою, так що

. (16)

в) Розглянемо тепер дипольний момент, який індукується на провідній сфері однорідним електричним полем . Знайдемо потенціали і поля зовні і зсередини сфери. Приймемо до уваги, що розподіл зарядів на поверхні сфери є вісе-симетричним, внаслідок чого потенціали є функціями відстані від центра сфери до довільної точки і кута між відповідним радіусом-вектором і вектором :

, .

Потенціали і задовольняють рівнянням Лапласа:

, ,

і граничним умовам:

, (17)

. (18)

Враховано, що в рівновазі потенціал провідної сфери повинен бути однаковим в різних точках. Потенціали і , як розв’язки рівнянь Лапласа, мають структуру:

,

де - поліноми Лежандра, , , …

З умови обмеженості потенціалів при і , випливає, що

, (19)

, (20)

Враховуючи постійність потенціала на поверхні сфери, знаходимо, що відмінними від нуля є тільки , і , причому = і . Таким чином,

,

.

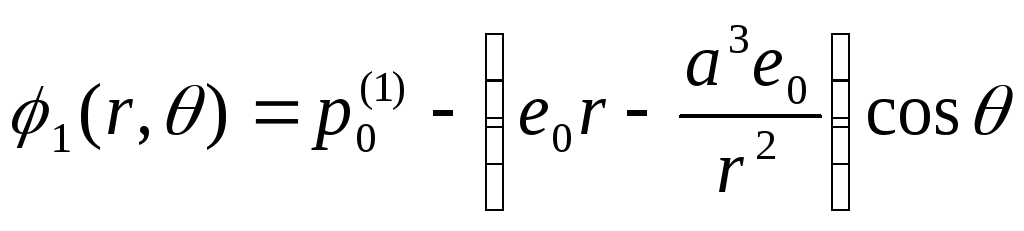Оскільки далеко від сфери потенціал поля повинен співпадати з потенціалом зовнішнього поля, то константу треба прирівняти нулю. Доданок до потенціалу зовнішнього поля на великих відстанях від сфери:

співпадає з потенціалом диполя, дипольний момент якого дорівнює:

. (21)

Коефіцієнт пропорційності в (21) інтерпретується як коефіцієнт поляризує- мості провідної сфери в зовнішньому однорідному електричному полі.

г) Знайдемо тепер ємність конденсатора у присутності провідної сфери. Заряджений конденсатор на великій відстані від нього утворює поле диполя:

, де , - одиничний вектор, перпендикулярний до обкладинок конденсатора. Напруженість поля в околі провідної сфери, таким чином, дорівнює:

.

Згідно (19) сфера набуває індукованого дипольного моменту:

.

В свою чергу в околі плоского конденсатора сфера утворює квазі-однорідне зовнішнє поле:

.

Згідно (16) це поле призводить до зміни різниці потенціалів між обкладинками конденсатора на величину:

Таким чином, ємність плоского конденсатора в присутності провідної сфери дорівнює:

.

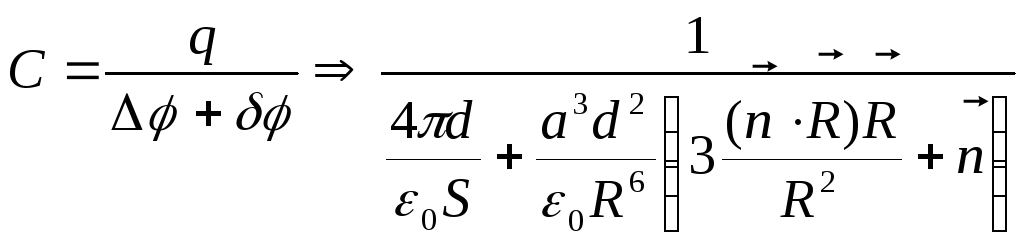Враховуючи малість доданку, можна написати:

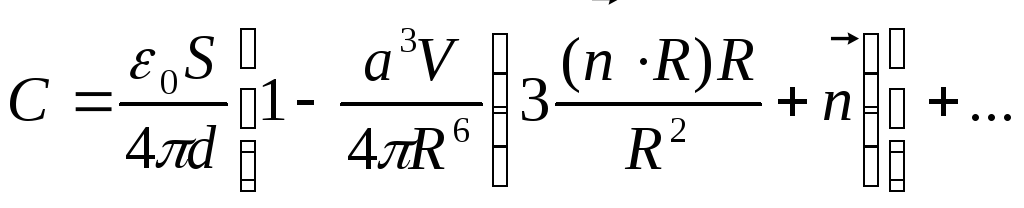, (22)

де - об’єм плоского конденсатору.

Задача 3. Дві сфери, радіуси яких дорівнюють і , знаходяться на відстані одна від одної. Сфери отримують заряди і . Знайти потенціали сфер, а також потенціальні і ємнісні коефіцієнти.

Розв’язок:

Розв’язок цієї задачі передбачає знаходження потенціалу зовні обох сфер і всередині кожної з них. Для вирішення цих задач бажано скористатись бісферичною системою координат, що є дуже громіздким.

Замість цього ми скористаємось наближеним підходом. На першому кроці поле першої сфери (радіуса ) будемо вважати відомим. Вносимо в нього другу сферу і розраховуємо ті зміни, до яких це призводить. На другому кроці будемо вважати фіксованим поле вже другої сфери і розраховуємо поправки до вихідного поля першої сфери. Далі ця процедура може бути продовженою стільки раз, скільки вимагає точність розв’язку задачі.

а) Знайдемо потенціали сфери на першому кроці. Нехай сфера радіуса отримує заряд . Вихідний потенціал сфери і зовні сфери дорівнюють:

, .

В околі точки цей потенціал приймає вигляд:

. (23)

Потенціал зовні і всередині другої сфери задається розкладами (див. (19) і (20)):

(24)

і

. (25)

Як і завжди, коефіцієнти розкладів знаходимо з граничних умов:

(26)

. (27)

Тут враховується, що на провідній сфері значення потенціалу є фіксованим.

З (25) і (26) легко знаходимо:

. (28)

Так само, з (23), (24) і (26) випливає, що

, , (29)

і

. (30)

Для знаходження коефіцієнтів і врахуємо, що сумарний заряд, індукований на сфері радіуса , повинен дорівнювати нулю, тобто

.

Разом з (27), це призводить до значення:

,

а також

. (31)

Таким чином, внесення другої сфери в електричне поле першої сфери, як це випливає з (25), (28) і (31), призводить то того, що сфера набуває потенціал:

. (32)

Внаслідок перерозподілу заряду на другій сфері буде змінюватись і потенціал першої сфери, але цей ефект буде більш високого порядку малості.

Якщо друга сфера отримує власний заряд її потенціал буде становити:

. (33)

В тому ж наближенні, потенціал першої сфери дорівнюватиме:

. (34)

Другі доданки в формулах (33) і (34) описують вплив однієї сфери на другу.

Рівняння (33) і (34) можна переписати, також, у вигляді:

(35)

(36)

Надамо рівнянням (33) і (34) матричного вигляду:

, , (37)

де

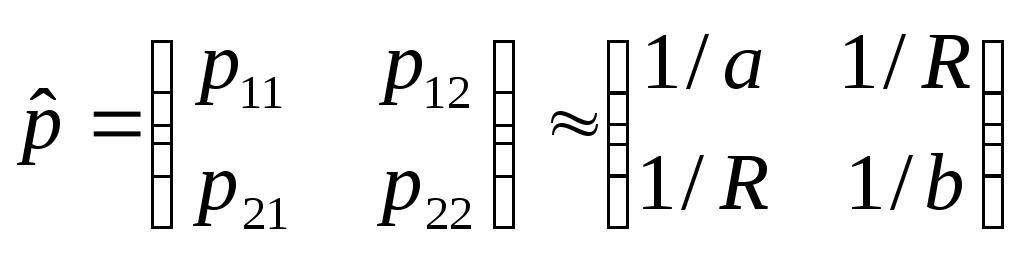(38)

будемо називати матрицею потенціальних коефіцієнтів.

Так само можна подати і рівняння (35), (36):

, , (39)

де

- (40)

матриця ємнісних коефіцієнтів. За своїм смислом матриця є взаємно оберненою по відношенню до :

, (41)

і навпаки

. (42)

Матриці потенціальних (38) і ємностних (40) коефіцієнтів задовольняють цим умовам тільки наближено. Так

(43)

відрізняється від (38) внесками порядку , що є наслідком наближеного методу знаходження потенціальних і ємнісних коефіцієнтів.

б) На другому кроці розрахуємо зміну потенціалу першої сфери під впливом поля індукованих зарядів другої сфери. З формул (24) і (29) випливає, що електричне поле, утворене індукованими зарядами другої сфери, описується

формулою

. (44)

Вводячи заряд-зображення

,

який знаходиться в точці

,

формулу (44) можна переписати у вигляді:

, (45)

де . В області знаходження першої сфери потенціал (45) трансформується в поле диполя:

, (46)

де - дипольний момент другої сфери.

Неважко впевнитись, що потенціал першої сфери змінюється на величину:

. (47)

Аналогічно буде змінюватись і потенціал другої сфери під впливом індукованих зарядів першої сфери. Таким чином,

, (48)

, (49)

а відповідні потенціальні коефіцієнти і дорівнюють:

, . (50)