Для студентов / Методички / (2)Методичка - СТО-УКР / (3)CTO(укр)

Задача 9. Ракета рухається прямолінійно з постійним прискоренням відносно своєї супроводжуючої системи. Скільки часу (за «земним годинником») ракета буде набирати швидкість: ?

Розв’язок:

Скористаємось формулою (), яка встановлює зв'язок між прискоренням ракети в ССВ і ЛСВ, яка пов’язується з Землею:

, (55)

і врахуємо, швидкість ССВ відносно Землі співпадає зі швидкістю ракети в даний момент часу : . Оскільки , то (55) можна переписати у вигляді рівняння для швидкості ракети:

, . (56)

Після розділення змінних

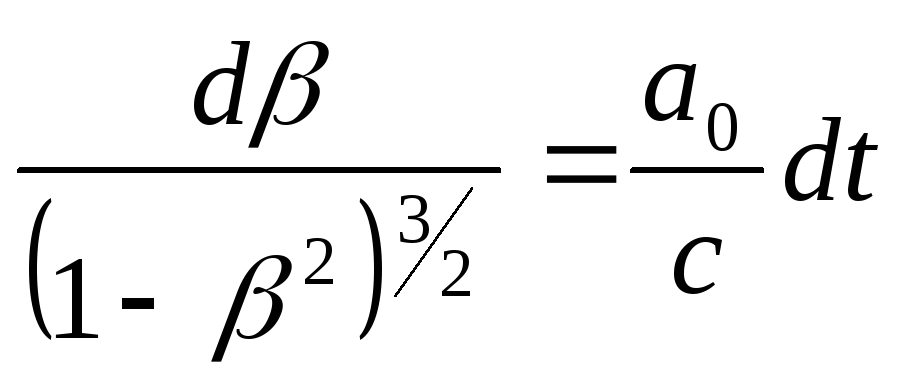
воно легко інтегрується:

, (57)

де - постійна інтегрування. Приймаючи, що при ракета є нерухомою, ми знаходимо, що . Неважко бачити,що залежність швидкості ракети від часу описується рівнянням:

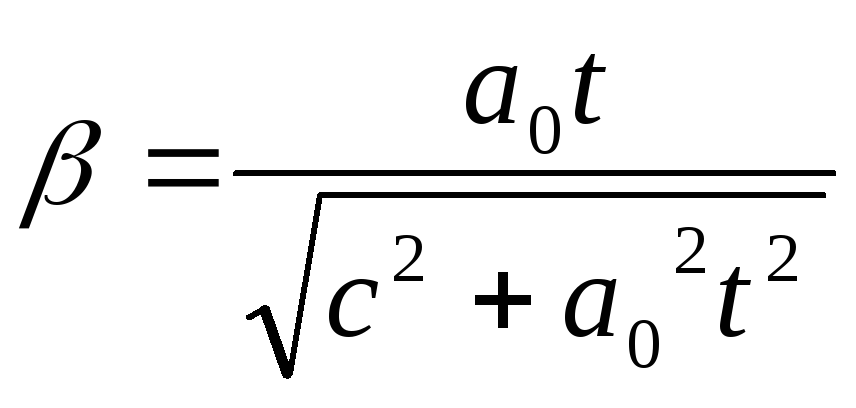. (58)

Час розгону ракети до швидкості безпосередньо знаходиться з (57):

.

Підставляючи в неї , знаходимо:

. (59)

Задача 10. Узагальнити перетворення Лоренца на випадок довільної орієнтації вектора відносно систем та .

.

Розв’язок:

Перетворенням Лоренца (7) і (8) можна надати наступне нове тлумачення. Координати точки можна інтерпретувати як проекції радіус-вектора точки на напрямок вектора швидкості (-координата) і на площину, перпендикулярну до ( і - координати). У згоді з цим радіус-вектор представляється у вигляді суми

, (61)

де і – його складові, направлені вздовж вектора швидкості і перпендикулярно до нього.

Так само можна розкласти і вектор :

. (62)

Поздовжня і поперечна проекції та радіус-вектора перетворюються подібно до координат точки та у формулах (7) і (8), тобто

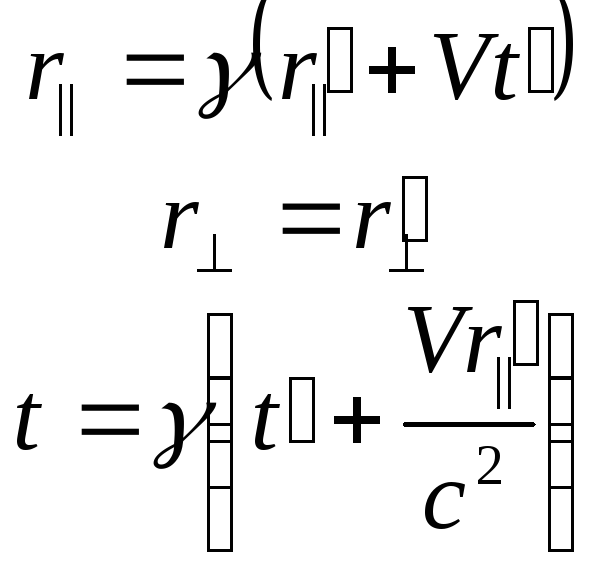, (63)

Оскільки вектор швидкості точки може бути направленим у просторі будь-яким чином, формули (63) бажано переписати у векторній формі:

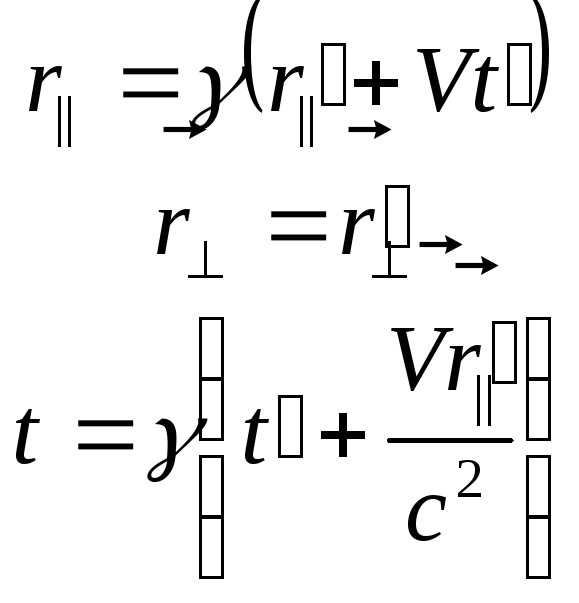, (64)

З (64) і (61) та (62) випливає, що

(65)

і

, (65)

де враховано, що .

Побудуємо тепер поздовжні і поперечні складові радіус-вектора у явному вигляді. Введемо одиничний вектор , направлений вздовж швидкості відносного руху ІСВ та . Тоді проекція радіус-вектора на напрямок швидкості дорівнює: , а сама поздовжня складова представляється добутком проекції на відповідний одиничний вектор:

. (66)

У згоді з цим поперечна складова радіус-вектора має структуру:

.

Подібні формули мають місце і для

, . (67)

Підставляючи (67) у (65), отримаємо шукане перетворення

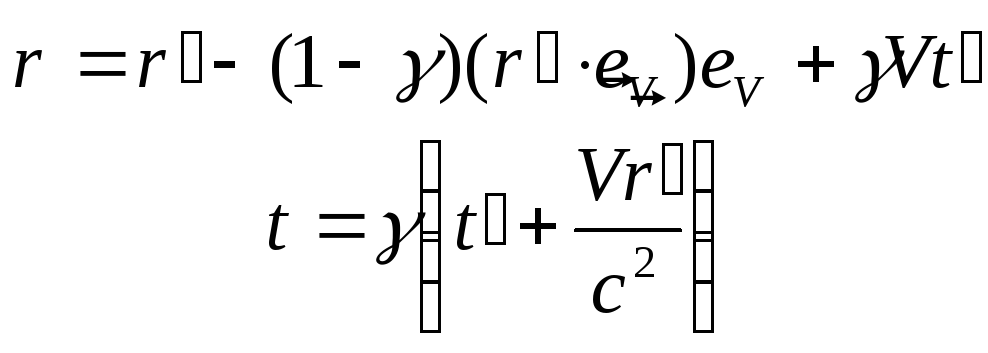(71)

Задача 11. Знайти закон перетворення швидкості точки у випадку довільної орієнтації вектора відносно систем та .

Розв’язок:

Для одержання відповіді на поставлене питання достатньо обчислити диференціали і , спираючись на формули (71), і поділити перший з них на другий. В силу лінійності співвідношень (71), диференціали і дорівнюють:

, (72) . (73)

Поділимо тепер на і врахуємо означення векторів швидкостей в системах відліку та : і . Після тривіальних перетворень знаходимо:

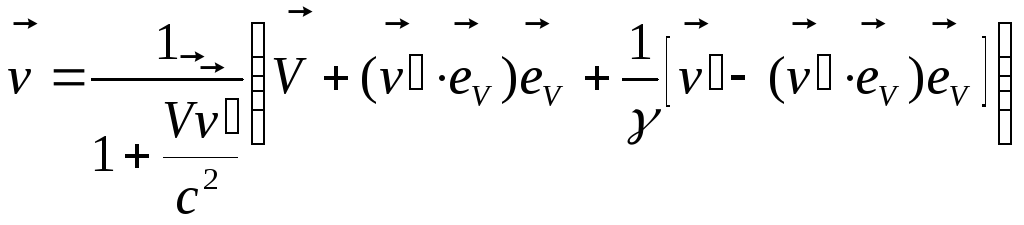. (74)

Це і є загальна формула закону додавання швидкостей у випадку довільної орієнтації вектора відносно систем відліку та .

Чотиривимірні вектори (чотири-векторы)

а) чотиривимірний радіус-вектор. З метою спрощення кінематики спеціальної теорії відносності є доцільним перейти від просторових координат точки і змінної часу до 4-х однотипних координат , утворених за правилом: , , і , де - уявна одиниця. Сукупності координат ставиться у відповідність 4-х радіус-вектор . Квадрат його довжини визначається стандартним чином: , де , а по індексам, що повторюються, виконується сумування: .

Перепишемо тепер перетворення Лоренца (7) і (8) у 4-х вимірному вигляді. З алгебраїчної точки зору перетворення Лоренца мають лінійний характер, тому у 4-х вимірному просторі вони набувають матричної форми:

, (76)

де і є компонентами 4-х радіус-вектора в ІСВ і відповідно. Неважко впевнитись, що матриця перетворення має вигляд:

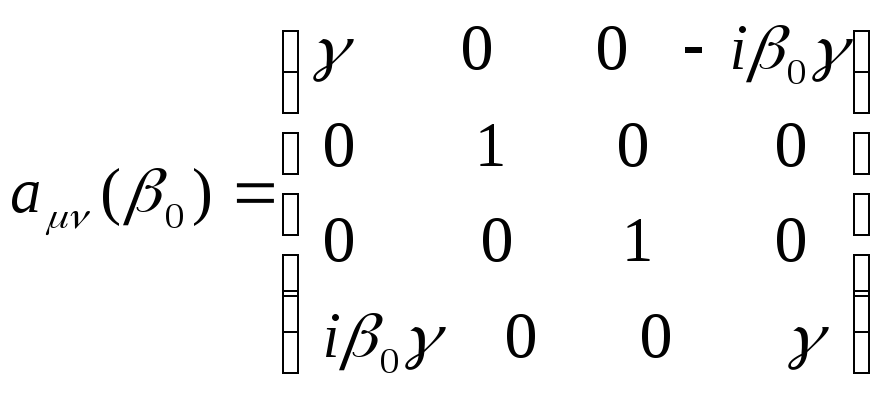, (77)

де, як і раніше, і

Оберненому перетворенню:

, (78)

відповідає матриця , яка відрізняється від (77) тільки знаком відносної швидкості однієї ІСВ відносно другої, тобто . Переходу від до в (77) формально відповідає операція транспозиції матриці: , або . За своїм смислом є матрицею, оберненою до , що дозволяє написати наступні співвідношення:

.

Квадрат інтервалу для нескінчено близьких подій представляється у вигляді:

, (79)

тобто, квадрат диференціала 4-х радіус-вектора є інваріантним відносно перетворень Лоренца, або перетворень (76) чи (78).

Оскільки

, (80)

то матриця повинна задовольняти наступним умовам ортогональності:

і . (81)

Друге з рівнянь (81) можна записати у вигляді

. (82)

Виходячи з того, що детермінант добутку матриць дорівнює добутку детермінантів: , а , з (82) знаходимо: , або . Оскільки при перетворення Лоренца стає тотожнім і для нього , ми робимо висновок, що завжди

. (83)

В справедливості (83) можна переконатись і прямим підрахунком на основі (77).

Якщо набір яких-небудь чотирьох величин при переході від однієї ІСВ до іншої перетвор.ється як чотири-радиус-вектор, то кажуть, що величини утворюють чотирих-вектор. Тобто усі чотири-вектори перетворюються за законом

; . (81)

Диференцюючи обидів частини (81), бачимо, що диференціали компонент будь-якого чотири-вектора утворюють чотири-вектор. В окремісті, чотири-вектор утворюють величины :

. (82)

З урахуванням (71) формулу (78) можна узагальнити на випадок довільного напрямку відносної швидкості :

, (79)

де

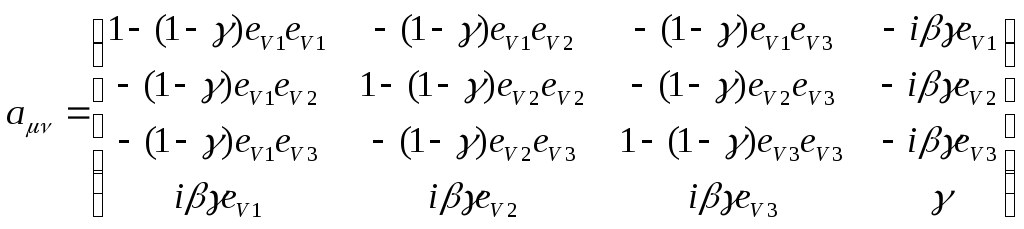. (80)