Для студентов / Методички / (2)Методичка - СТО-УКР / (1)CTO(укр)

РОЗДІЛ 1. РЕЛЯТИВІСТСЬКА КІНЕМАТИКА

Перетворення координат, часу та швидкості

Наведемо порівняльні характеристики перетворень Галілея, які пов’язують час і просторові координати точки в двох різних інерціальних системах відліку класичної фізики, з перетвореннями Лоренца, які відігріють ту ж саму роль в фізиці, яка спирається на Айнштайнівські постулати відносності.

а) перетворення Галілея. Розглянемо дві інерціальні системи відліку (ІСВ) та , яки рухаються відносно одна одної так, як показано на Рис. 1. Нехай – швидкість системи відносно системи , яку ми будемо вважати

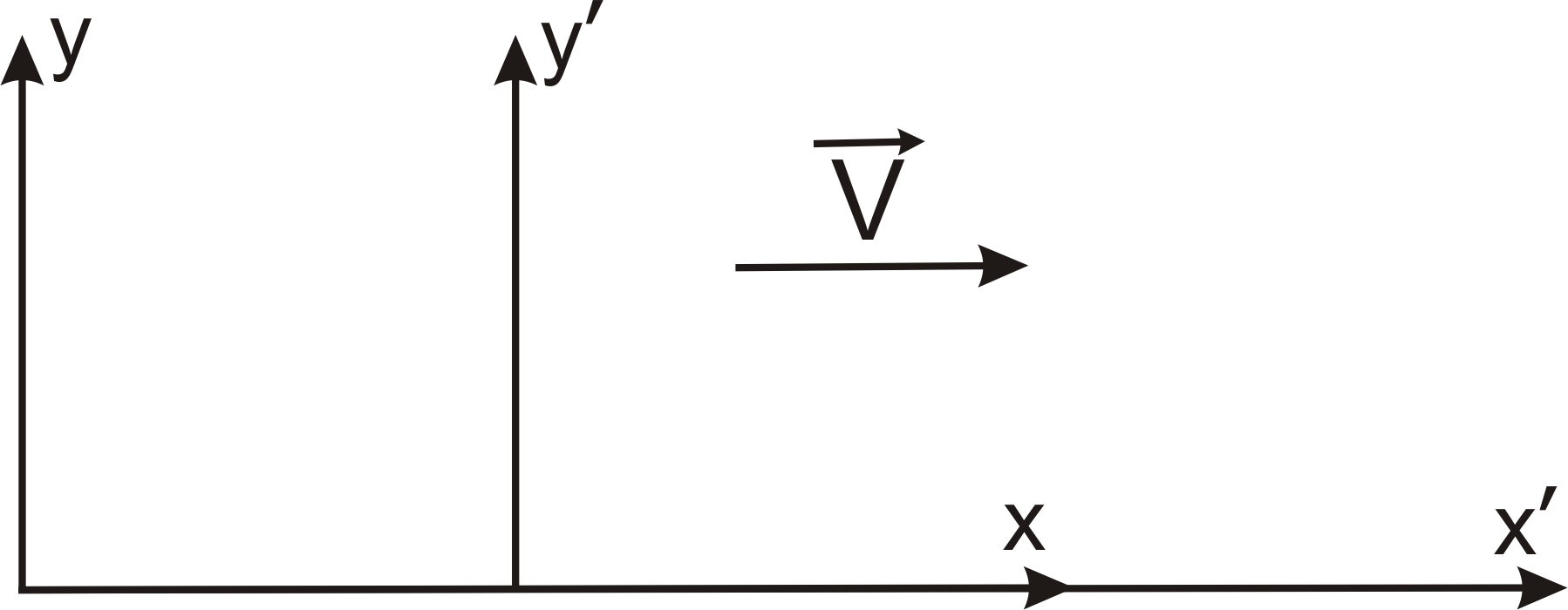
Рис. 1. Взаємний рух двох інерційних систем відліку.

нерухомою. Припускається, що годинники в ІСВ та синхронізовані, при чому у момент, коли точки та збігалися, вони показували . Принципово важливим є питання відносно того, як перетворюються координати та час материальної точки при переході від однієї системи до іншої.

В класичній механіці постулюється, що плин часу має абсолютний характер, а зв'язок між просторовими координатами надається формулами

(1)

Перетворення (1) називаються перетвореннями Галілея.

Виконуючи диференціювання (1) за часом, отримуємо закон перетворення компонент швидкості:

. (2)

Відстань між двома точками і в ІСВ дорівнює:

; (3)

Так само визначається відстань між тими ж самими точками в ІСВ :

. (4)

Підставляючи в праву частину вираз (3) значення координат (1), отримаємо праву частину виразу (4), тобто .

Величини, які не змінюють свого значення при перетвореннях координат і часу, називають інваріантами відповідного перетворення. Таким чином, відстань між двома матеріальними точками є інваріантом перетворень Галілея.

Оскільки кінці жорсткого стержня можуть служити прикладом двох просторових точок, ми робимо висновок, що його довжина є інваріантом перетворень Галілея. В найпростішому випадку, коли стержень орієнтується вздовж вісі -ів, його довжина визначається різницею координат його кінців: . (5)

З (1) також випливає, що , тобто проміжки часу є також інваріантними відносно перетворень Галілея.

З (1) випливає і класичний закон додавання швидкостей. Якщо швидкість точки в ІСВ дорівнює , то її швидкість в ЛСВ визначається за формулою:

, (6)

де . Перетворення Галілея, одначе, знаходяться у протиріччі з постулатами спеціальної теорії відносності (СТВ)

б) перетворення Лоренца. В релятивістській фізиці, яка спирається на Айнштайнівські постулати відносності, перетворення Галілея змінюються на перетворення Лоренца:

, (7)

де введено позначення , .

Обернене перетворення має вигляд

. (8)

Безпосередньо з (7) і (8) видно, що відстань між двома просторовими точками і проміжки часу, які визначаються за формулами класичної фізики, не є інваріантними відносно перетворень Лоренца. Більш того, відстань між двома просторовими точками починає залежати від часу, а проміжки часу – від координат точки, що з фізичної точки зору є неприйнятним. Звідси випливає, що в рамках теорії відносності, заснованій на Айнштайнівських постулатах, повинні бути встановлені нові означення довжини рухомого об’єкту і проміжків часу між двома подіями.

Довжина нерухомого стержня визначається за різницею показань прикладеної до нього лінійки. Якщо стержень, або якийсь інший фізичний об’єкт рухається, то прикласти до нього лінійку неможливо (її можна прикласти тільки в системі відліку, відносно якої стержень є нерухомим). Ця проблема особливо загострюється, коли швидкість стержня є більшою від характерних швидкостей, властивих вимірювальному приладу. Але координати початку і кінця стержня можна визначити, зробивши його миттєву фотографію. Довжиною рухомого стержня потрібно називати саме різницю координат його кінця і початку, визначених за допомогою миттєвої фотографії.

ІСВ, відносно якої тіло в даний момент часу є нерухомим, будемо називати супроводжуючою системою відліку (ССВ). Довжину стержня, яку вимірюють у ССВ за допомогою нерухомої відносно тіла лінійки, називають його власною довжиною.

Нехай стержень, що має власну довжину , рухається відносно лабораторної системи відліку (ЛСВ) із швидкістю так, як показано на Рис. 2. В ЛСВ довжина стержня , за означенням, дорівнює:

, (9)

де та – координати начала та кінця стержня відповідно, які вимірюються в один і той же момент часу за показаннями годинника ЛСВ. Саме такі координати точок визначаються за допомогою швидкісного фотографування стержня нерухомим спостерігачем в ЛСВ.

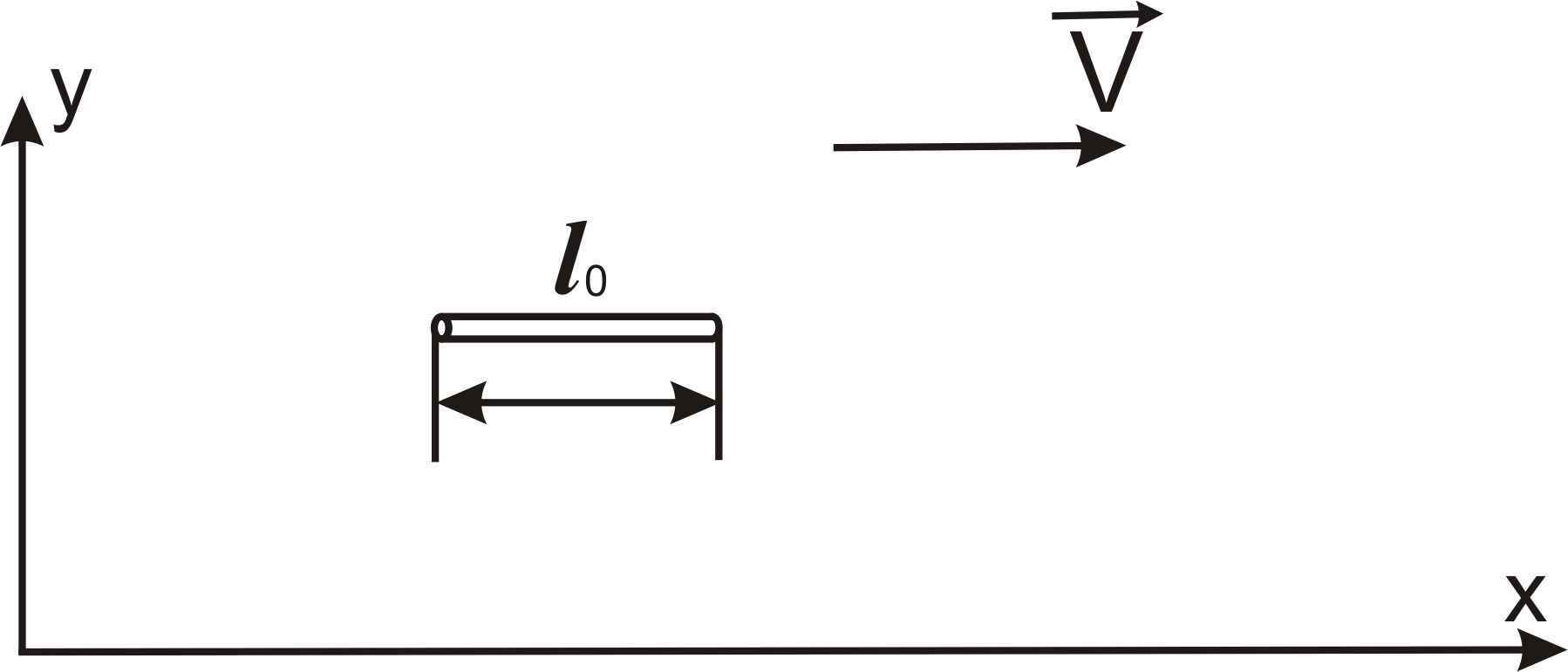
Рис. 2. Рух стержня відносно ЛСВ.

Напрямок стержня та його швидкості збігається з напрямком вісі X .

При фіксованому значенні з (8) випливає

, (10)

тобто, у згоді з означенням, або

. (11)

Таким чином, довжина стержня є максимальною в ССВ . В ЛСВ вона зменшується з ростом швидкості стержня . Це явище називається лоренцевим скороченням.

З перетворень Лоренца випливає, що у випадку, кола стержень є орієнтованим перпендикулярно вектору швидкості, скорочення його довжини не відбувається: , оскільки .

Перейдемо тепер до визначення співвідношення між проміжками часу в різних ІСВ. Проміжок часу між двома подіями 1 і 2, який вимірюється нерухомим відносно тіла годинником, називається власним проміжком часу.

Нехай ІСВ , відносно якої тіло є нерухомим, зміщується відносно ЛСВ зі швидкістю , а події 1 і 2 відбуваються в моменти часу і відповідно. За означенням, проміжок часу між подіями 1 і 2 в ЛСВ визначається як різниця показань і нерухомого відносно ЛСВ годинника, які відповідають одному й тому ж місцезнаходженню годинника в ІСВ . Таким чином,

. (12)

З (7) випливає, що

,

тобто

. (13)

При наближенні швидкості тіло до світлової () . Відбувається так зване релятивістське уповільнення часу.

Закон додавання швидкостей теж модифікується. Переходячи від (7) і (8) до диференціалів координат і часу

, , ,

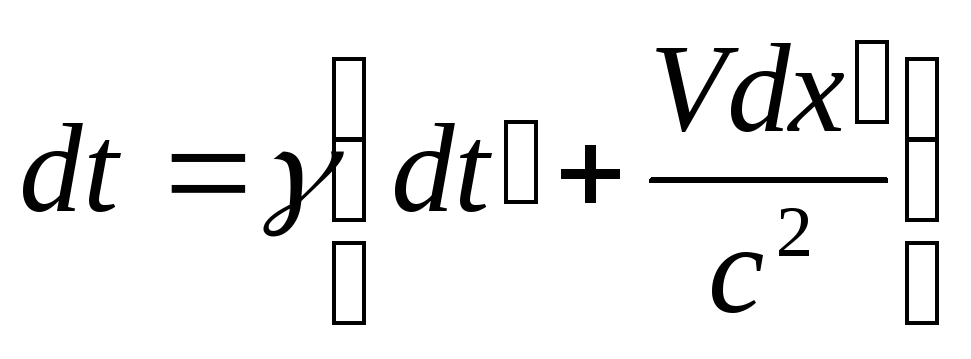
і використовуючи стандартні означення та , для компонентів швидкості в системах відліку та знаходимо:

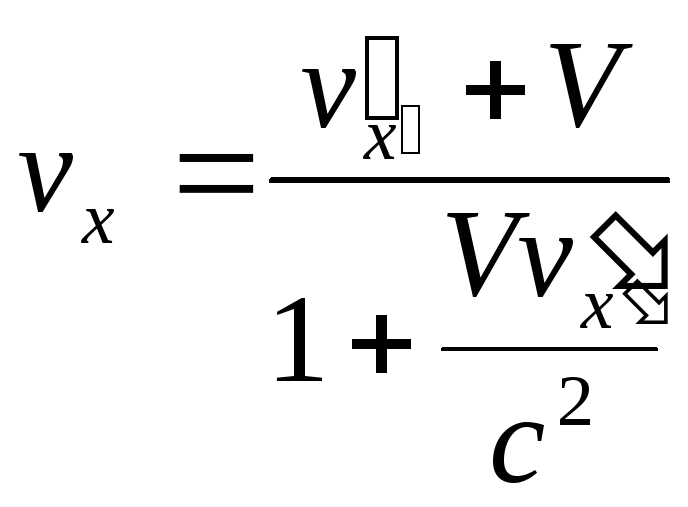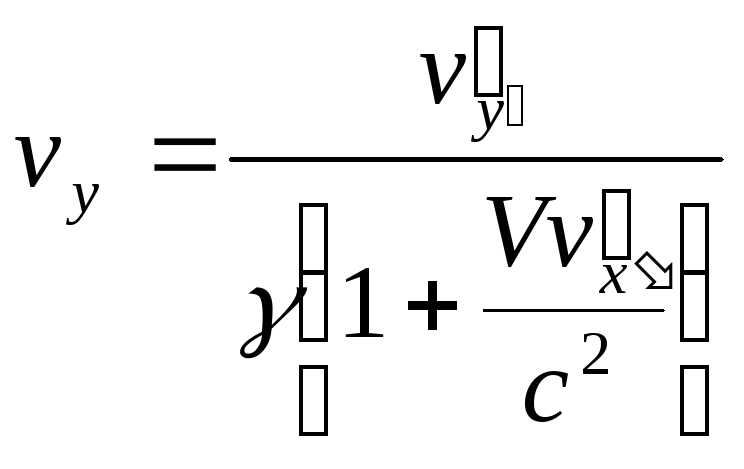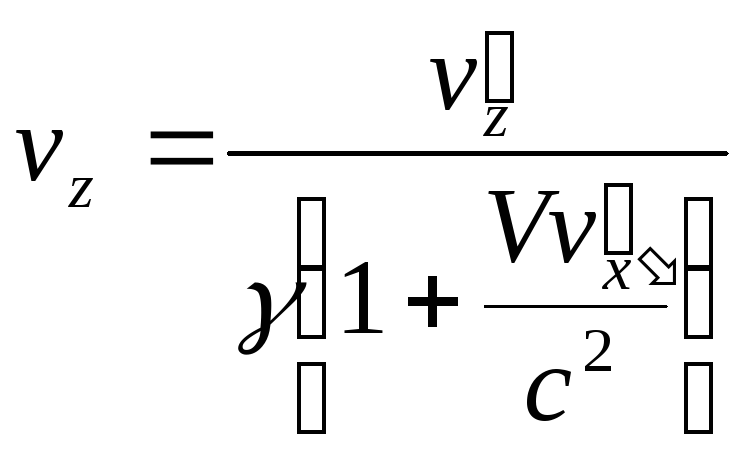, , . (14)

Підкреслимо, що в граничному випадку, коли , формули (11), (13) і (14) переходять до (6), тобто кінематика класичної фізики є граничним випадком для кінематики спеціальної теорії відносності.

в) Просторово-часовий інтервал. Нехай та будуть координатами яких-небудь двох подій. За означенням, просторово-часовим інтервалом , або просто інтервалом, між цими подіями називається величина, що задається співвідношенням:

. (15)

Найважливішою властивістю інтервала є те, що він є інваріантним відносно перетворень Лоренца.

Для двох нескінченно близьких подій інтервал приймає вигляд:

, (16)

де - швидкість об’єкта в ЛСВ.

Задача 1. Стержень, власна довжина якого дорівнює , рухається відносно деякої ІСВ із швидкістю . Найти довжину стержня в системі , якщо:

а) кут між напрямком стержня та вісью в системі дорівнює (рис.3а),

б) кут між напрямком стержня та вісью в системі дорівнює (рис.3б);

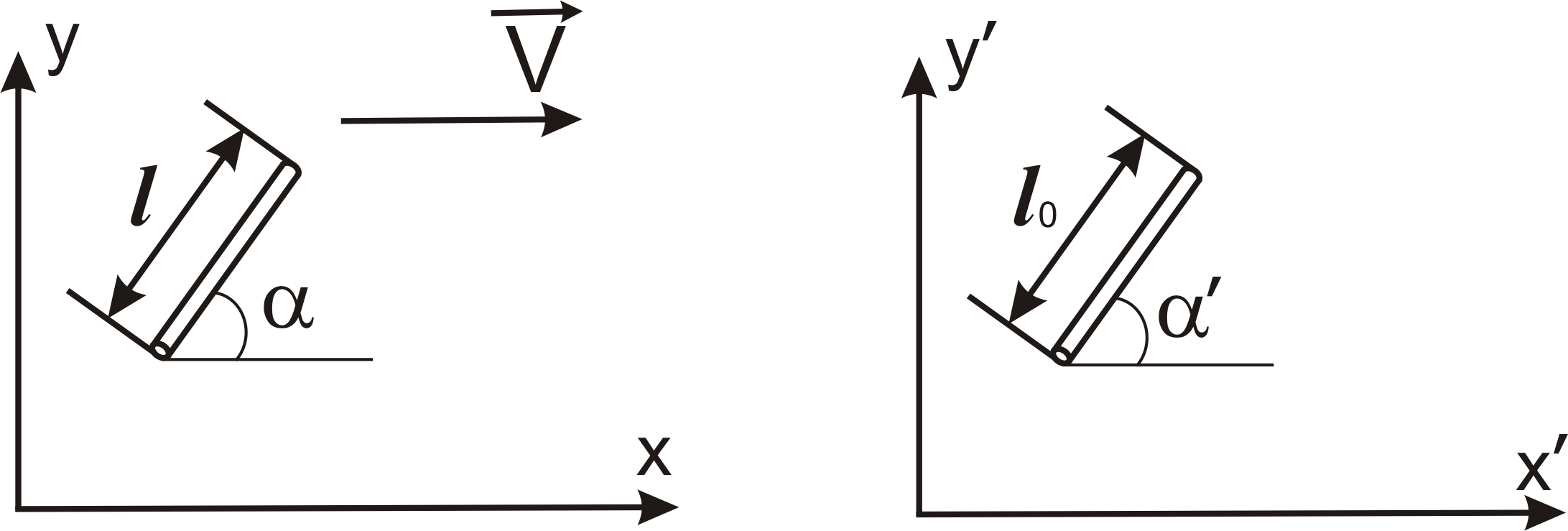
а) б)

Рис. 3. Рух стержня, напрямок якого не співпадає з вісью :

(а) – в ЛСО; (б) – в ССО.

Розв’язок:

а) Довжина стержня в системі може бути представлена у вигляді

, (10)

де і , складові, направлені вздовж швидкості і перпендикулярно їй. В системі має місце аналогічне співвідношення 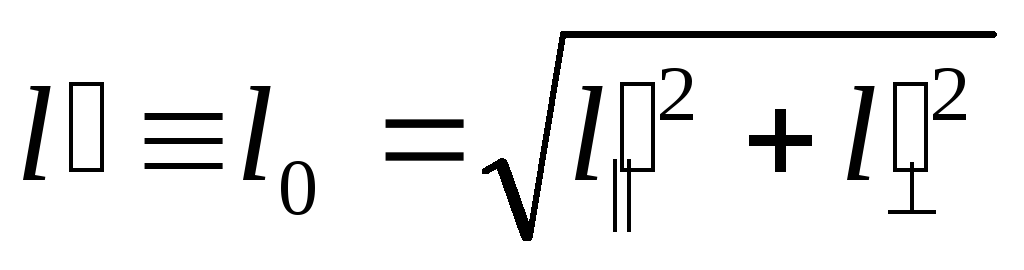, де

і . (11)

Вище було показано, що поздовжна складова довжини стержня змінюється за законом

, (12)

а поперечна залишається незмінною:

. (13)

Таким чином, закон перетворення довжини стержня має наступний вигляд:

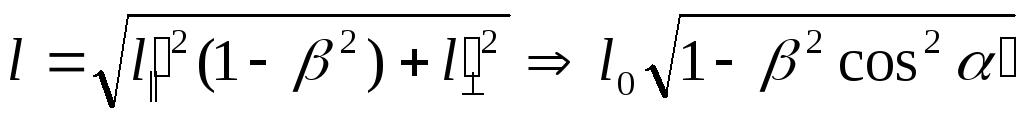. (14)

В граничних випадках, коли стержень є орієнтованим вздовж швидкості його руху () і перпендикулярно до неї (), значення його довжини, як і повинно бути, співпадають зі знайденими вище.

б) Тут також потрібно скористатись законами перетворення (12) і (13) поздовжніх і поперечних складових довжини стержня. Але на відміну від (12) і (13) перепишемо їх у вигляді

, (15)

Поздовжні і поперечні складові довжини стержня в системі пов’язані з стандартним чином:

і . (16)

Довжина стержня в , яка є супроводжуючою системою відліку для нього, співпадає з його власною довжиною: . З іншого боку, дорівнює

, (17)

Підставляючи в (17) значення і , які надаються формулами (15) і (16), отримуємо:

. (18)

Після тривіальних перетворень (18) остаточно знаходимо наступне значення довжини стержня в системі :

. (19)

В граничних випадках () і () результат (19) повністю погоджується з отриманими вище оцінками.

Задача 2. ІСВ рухається відносно «нерухомої» ІСВ зі швидкістю , що направлена вздовж їхніх і осей. В ІСВ вздовж її вісі на протязі з постійною швидкістю рухається матеріальна точка. В момент часу вона знаходилась в точці , яка, в свою чергу, співпадала з початком координат ІСВ . Знайти:

1. закон руху материальної точки в обох ІСВ,

2. співвідношення між часами руху та пройденими шляхами.

Розв’язок:

В ІСВ закон руху точки має тривіальний вигляд:

. (20)

Для находження закону руху в ІСВ підставимо (20) у перетворення Лоренца (5):

, (21)

. (22)

Шуканий закон руху знаходиться шляхом виключення з (21) і (22) спільного множника . Таким чином,

, (23)

де

(24)

є швидкістю руху точки відносно ІСВ . Формула (24) представляє собою результат релятивістського складання швидкостей точки і системи відліку і, як і повинно бути, співпадає з першою з формул (14).

Співвідношення між проміжками часу та руху точки безпосередньо прямує з (22):

, (25)

де , , . Тут доречно скористатись наступною тотожністю (яка перевіряється елементарним чином):

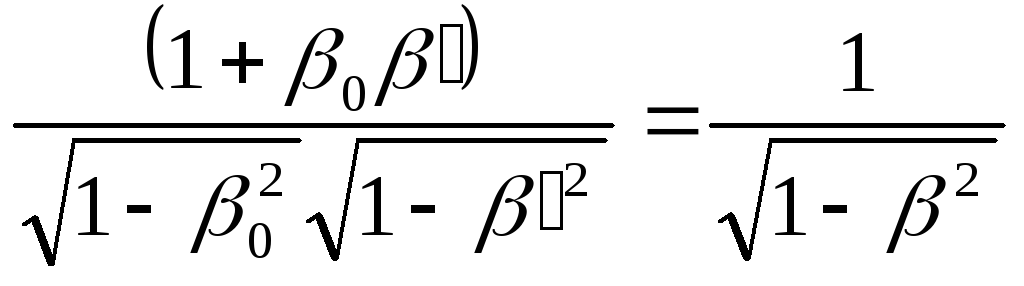, (26)

де . Як наслідок, формула (25) приймає вигляд:

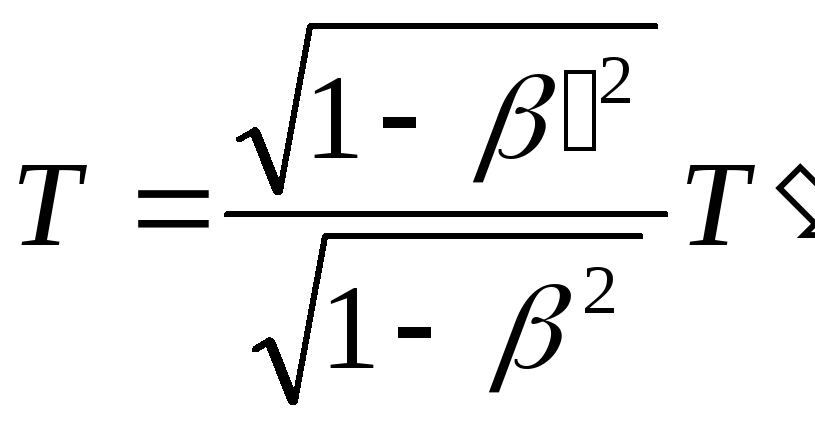. (27)

Якщо точка буде нерухомою в ІСВ , то та . У цьому випадку, формула (27) переходить у стандартний закон перетворення проміжків часу (10).

Підставляючи в (21) , знаходимо наступне співвідношення між пройденими шляхами:

. (28)

Як бачимо, воно вельми суттєво відрізняється від стандартного закону перетворення довжин відрізків (11).

Для більш чіткого розуміння причини такої відмінності, обчислимо у такий самий спосіб відстань між двома точками в ЛСВ , якщо вони рухаються відносно неї з однаковою швидкістю і в ССВ їх розділяє відстань .

Нехай в початковий момент часу точка, яка рухається в ІСВ зі швидкістю , має координату . Тоді формули перетворення (21) і (22) переходять у

, (29)

. (30)

Виключаючи , знаходимо наступний закон руху матеріальної точки в ІСВ :

, (31)

де, як і раніше, . Так саму структуру має і закон руху другої матеріальної точки

, (32)

для якої =. За означенням, відстань між вказаними точками становить:

.

Підставляючи сюди значення координат точок з (31) і (32), знаходимо:

. (33)

Якщо точки та рухаються разом з ІСВ , тобто їх швидкість відносно ІСВ дорівнює нулю, то і відстані між точками, які задаються формулою (33), задовольняють співвідношенню: , тотожному (11).