Практикум по математическому анализу

Практикум по математическому

анализу

Функция. Способы задания. Классификация функций. Числовая последовательность

1.Способы задания функций. График функции.

2.Классификация функций.

3.Числовая последовательность. Предел числовой последовательности.

Теоретическая часть:

Функция одной переменной: основные понятия

Множество действительных чисел х, удовлетворяющих неравенству а≤х≤b,

называется отрезком и обозначается [ a;b ].

Множество

действительных чисел х,

удовлетворяющих неравенству

a<х<b, называется интервалом и обозначается (а; b).

Интервал

( x - ; x )

, где

> 0 называется

- окрестностью точки х.

Тогда

- окрестностью + называется

(

;+ );

- окрестностью -

называется (- ; - ); - окрестностью называется (-

; -

)U( ;+ ).

Величины в математике делятся на постоянные и переменные. Постоянной называется величина, которая в условиях данного

эксперимента сохраняет одно и то же значение.

Переменной называется величина, которая в условиях данного эксперимента может принимать различные значения.

Рассмотрим две переменные величины х и у и пусть у зависит от х. Зависимость у от х, при которой каждому значению переменной х

соответствует единственное, вполне определенное, значение переменной у,

называется функциональной.

Пусть даны два множества Х и У.

Определение: Функцией, отображающей Х в Y, называется соответствие, при котором каждому элементу хєХ соответствует единственный элемент уєY. Обозначается это так: f : X Y . Множество Х называется областью определения функции, множество Y – областью значений функций. Значение функции в точке х обозначается f(x).

Способы задания функции бывают следующие:

1)	аналитический способ;
2)	графическое задание;
3)	табличный способ;
4)	перечисление множества пар вида x; f x и так далее.

Функция определяет однозначное соответствие в одну сторону, но не требуется, чтобы обратное соответствие в одну сторону, но не требуется, чтобы обратное соответствие тоже было однозначным. Однако, если

соответствие	f : X Y , определяемое данной функцией,			является взаимно
однозначным,	то	функция	называется обратимой,	а соответствие
Y X называется обратной функцией и обозначается f 1 .
Приняты обозначения: область определения - D f ; множество значений -
f . При этом всегда		f D f f	Y , где Y– область значений.

Если функция усмотрена из конкретной практической задачи, то ее область определения может быть заранее не дана. И тогда ее установить из данной задачи.

Если функция задана формулой и практическое происхождение формулы неясно, а также область определения функции не указана, то условились под областью определения этой функции понимать область определения соответствующего аналитического выражения.

			Классификация функций
Определение: Функция f называется неубывающей (невозрастающей)
на множестве Х,		если для любых х1 и х2 х1		Х , х2 Х . Из того, что	х2	x1
следует, что	f x2	f x1	f x2 f x1 .
f (x)		-	неубывающая	(невозрастающая)		на
def	x1 X x2 X x2 x1 f x2 f x1 ( f x2 f x1 ) .
X x1 , x2

Невозрастающие и неубывающие функции называются монотонными. Если в предыдущем определении между значениями функции будет

стоять знак строгого неравенства, то функция будет называться возрастающей и убывающей (функция тогда называется строго монотонной).

Определение: Функция f называется ограниченной на множестве Х, если множество ее значений f(x), принимаемых на данном множестве Х, является ограниченным.

Определение: Функция f называется четной (нечетной), если выполняется:

1) Область определения симметрична относительно точки х=0, т.е. x :

x D f x D f .

2)

x D f

:

f ( x) f (x)

f ( x) f (x)

График четной функции симметричен относительно оси ОY (осевая симметрия). График нечетной функции симметричен относительно начала координат (центральная симметрия).

Определение: Функция f называется периодической с периодом T>0, если:

1) x : x D f x T D f

2) x : x D f f (x T ) f x .

Числовая последовательность. Предел числовой последовательности

Определение: Числовой последовательностью называется заданная на множестве всех натуральных числе: f 1 , f 2 , f 3 , ..., f n , f n 1 , ...

функция,

или								, ... x
x	, x	2	, x	, ..., x	n	, x	n 1		n
1			3

xn - общий член последовательности.

Способы задания последовательности могут быть такие же, как и у других функций:

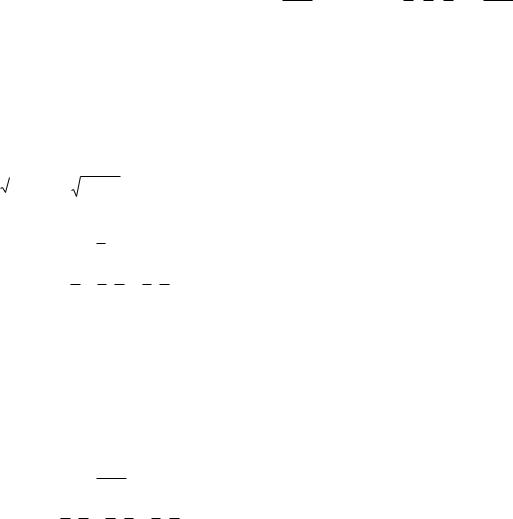
1. Аналитический. Например,

	x			n	,	т.е. x			1	,	2	,	3	, ...,	n	, ...
		n		n 1			n		2		3		4		n 1

2. «Кусочный». Например,

	1		, если n нечетное
		n
xn				x		1, 0,	1		1
	0		если n четное, т.е.					, 0,		, 0, ...
					n	3		5

Вотличие от других функций для последовательности есть

своеобразный способ

x1			xn 1		2 xn n N
	2;

Рассмотрим примеры:

задания	–	рекуррентный.	Например,
т.е.

1)

x	n

	x		1			n	1
		n					n
		1;		1	;		1
				2			3

(рис. 21)

	;	1	;	1	;	1	; ...
		4		5		6

Какую бы малую окрестность точки х=0 мы ни взяли, вне этой окрестности окажется лишь конечное число членов. Другой такой точки нет. Точка х=0 является пределом этой последовательности. Запишем это так:

lim 1 n

2)

3)

x	n

	1			0 .
	n							т.е. xn
	xn n,
	x			1				n		n
		n							n 1
					1	;	2		;	3	;	4
					2		3			4		5

1;2;3;4 ... Эта последовательность предела не имеет.

	;	5	;	6	; ... . Члены последовательности как угодно близко
		6		7

подходят к точкам 1 и -1.

Однако вне окрестности точки х=1 имеется бесконечное число членов данной последовательности. Поэтому 1 не является пределом этой последовательности, аналогично -1 тоже не является пределом.

Определение 1: Число а называется пределом последовательности xn ,

если какую бы малую окрестность точки а мы ни взяли, вне этой окрестности будет находиться лишь конечное число членов последовательности. Запишем

это так:

lim x	n	a

или xn a .

Если последовательность имеет предел, то она называется сходящейся.

В противном случае – расходящейся.	xn ,
Определение: Точка а называется пределом последовательности

если какую бы малую окрестность этой точки мы ни взяли, все члены последовательности. Начиная с некоторого номера, попадут в эту окрестность, т.е.

def

lim xn a U a, N n n N xn U a,

или

		def	N n n N x
lim x	n	a 0		n	a

1.Теорема: Всякая сходящаяся последовательность может иметь только один предел.

Если из данной последовательности удалить часть ее членов, так что в последовательности останется бесконечное число членов, и, если оставшиеся члены заново пронумеровать в прежнем порядке, то получится новая последовательность, которая называется подпоследовательностью данной последовательности.

2.Теорема:Если последовательность сходится, то любая ее подпоследовательность также сходится к тому же пределу.

3.Теорема:Всякая сходящаяся последовательность является ограниченной.

Замечание. Обратное утверждение неверно. Последовательность может

быть ограниченная, но расходящаяся. Например, xn 1 n .
			4. Теорема:Пусть даны		(xn ) и		уn .	Причем	n : xn yn , и пусть
	xn a, yn b . Тогда справедливо					a b .
			5. Теорема: Пусть	xn yn		zn .	Если	крайние	последовательности
	xn , zn имеют одинаковый предел, то и промежуточная последовательность yn
также сходится и имеет тот же предел.
			Определение: Последовательность n называется						бесконечно малой,
если она стремится к 0.
			Определение: Под окрестностью +∞ мы будем понимать любой
интервал вида Е, , где				Е 0	,	под окрестностью -∞ интервал , E , а
под окрестностью ∞ - объединение интервалов , E E, . Неравенство
	x		E означает: «х принадлежит Е – окрестности ∞».
			Определение: Последовательность				xn называется бесконечно большой,

если какую бы окрестность бесконечности мы ни взяли, вне этой окрестности останется лишь конечное число членов в последовательности.

Записывается это так:		lim xn	или	xn . Бесконечно	большая
последовательность является расходящейся.
Всякая	бесконечно	большая	последовательность		является

неограниченной. Обратное утверждение неверно, т.е. последовательность может быть неограниченной, но не стремиться к бесконечности.

Например:

1)1;2;1;3;1;4;1; ...

2)xn 1 1 n n , т.е. xn 0;4;0;8;0;12; ...

Теорема: 1) Если n - бесконечно малая последовательность, члены

которой отличны от нуля, то xn 1 - бесконечно большая.

n

2) Если

xn

- бесконечно большая последовательность, члены которой

отличны от нуля, то n		1		- бесконечно малая последовательность.
		x
			n

Практические задания:

1. Найти область определения функции:

а) f (x)

б)f(x)=

	1		ln(2x 1)
		2
	3x x		2
	2x
3 2x x2

в)f (x)=

	х		1
		3	х 3

lg(

2х

3

)

2. Для функции найти ей обратную

а) y 2x 5	б) y	x 3	в) y	4 5x
	2

3.Найти значение функции при данных значениях переменной:

f (x)=

lg(5 x)
x	2	x

, х=4; х=с

4.Исследовать функцию на четность, нечетность

х

4

3

2

f(x)=

x

ln(1

x

)

sin x

5.Даны функции, заполните таблицу:

1)y=3x2+sin x;

2) y+ln xy=cos

x

;

y

4)y=cos(2x+3);

5) y=(5x3+2x)ln x;

7) y=cos(x3+2y)-sin3x;

8)y=arccos(

3х2 2х

);

5х 3

3)y=tg(x2+7x);

6)y +5x+y=ln y;

x

9)y-3x2+cos3x=5.

	Функция		Функция	задана	Функция	Функция не
	задана	в			является	является
			в неявном виде
	явном виде				сложной	сложной

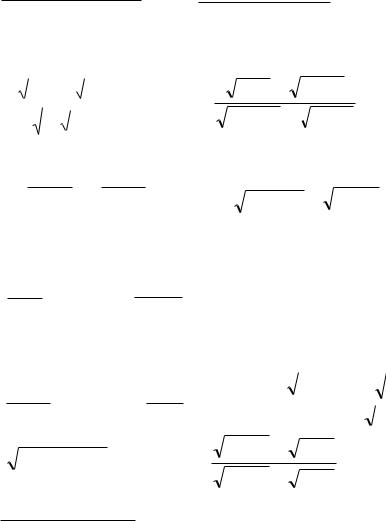
6. Вычислить пределы числовых последовательностей

1.

lim	(3 n)
		n)
n (3

2 2

(3 n)

(3 n)

2 2

.

2.

	(3 n)	4	(2 n)		4
lim						.
		4		4
n (1 n)			(1 n)

7. Вычислить пределы числовых последовательностей

1.

lim

n3

5n2

4 9n8 1

. 2.

n (n n)

7 n n2

	n 1				n	2	1
lim		3					5		.
n 3	3n		3		4	n		1

8. Вычислить пределы числовых последовательностей

1. limn n(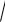n2 1 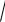n2 1) . 2.

lim n(	n(n 2)	n	2
n

3)

.

9. Вычислить пределы числовых последовательностей

1.

	n 1		n
lim		.
n	n 1

2.

		2n 3		n 1
lim		2n 1	.
n

Задания для самосоятельного решения:

1.

					n	4
	n	2	1
lim			2	.
n		n

2.

	n 1		n 2
lim		.
n	n 3

	lim		n5	8 n n(n2 5))
3.									.
						n
	n

4.

6.

	lim (		n	2
	n
		(3 n)				4
	lim
						3
	n (1 n)

3n 2

(2

(1

							n	3	1		n 1
n)				.	5.	lim		3				.
						n 3	n		1		n 1
n)		4
			.
n)	3

Предел функции в точке

1. Техника вычисления предела функции в точке

2.Техника вычисления предела функции на бесконечности.

Теоретическая часть:

Рассмотрим функцию y=f(x).Придавая переменной х различные значения, получим х1; х2; х3;...хn...- последовательность значений аргумента. Ей соответствует: f(x1);f(x2); f(х3); …; f(xn);… - последовательность соответствующих значений функции.

Если из того, что любая последовательность значений аргумента, взятая из области определения функции и -окрестности точки х0 (хn х0) сходится к х0 (x х0) следует, что последовательность соответствующих значений функции сходится к числу А (f(х) А), то число А называется пределом функции f(x) в точке х0.

Обозначение:

lim n x0

f(x)

A

.

Если

lim n x0

f(x)

0

, то функция f(х) называется бесконечно малой в

окрестности точки х0.

Например: функция у=х-4 при х

Если	lim f(x)		или	lim
	n x			n x
		0			0

4 является бесконечно малой.

f(x) , то функция называется

бесконечно большой в окрестности точких0.

Замечание. Данные выше определения справедливы и при x ± Бесконечно малые функции обладают следующими свойствами:

1) алгебраическая сумма любого конечного числа бесконечно малых функций в окрестности некоторой точки есть

бесконечно малая в окрестности той же точки;

.

функция

2)произведение любого конечного числа бесконечно малых функций в окрестности некоторой точки есть функция, бесконечно малая в окрестности той же точки;

3)произведение бесконечно малой функции в окрестности некоторой точки на функцию ограниченную, есть функция, бесконечно малая в окрестности той же точки.

Бесконечно малые функции в окрестности некоторой точки х0			(х) и
(х) называются бесконечно малыми одного порядка малости, если
lim	(x)	c 0 .
x x0	( x )

Если с=0 то		(х) называется
высокого порядка		малости по

бесконечно

сравнению с

малой функцией

(х). Бесконечно

более

малые

функции (х) и

	если	lim	(x)
			( x )
		x x0

(х) называются эквивалентными в окрестности точки х0,

1	. Обозначение:	( x ) ~ ( x )	.

Предел бесконечно малых (бесконечно больших) функций не изменится, если каждую из них заменить эквивалентной ей функцией т.е.

lim	f ( x )			lim	f1	( x )	,если f ( x ) ~ f1	( x ), ( x ) ~ 1( x ) .
	( x )				( x )
x				x 1

При вычислении пределов функций обычно пользуются следующими основными теоремами о пределах:

если	lim	f (
	x x
	0

1) lim c

x x0

x ) и	lim q( x ) существуют и конечны, то
	x x0

c , где c=const.

2)	lim c f(x) c lim f ( x ) .
	x x0	x x0

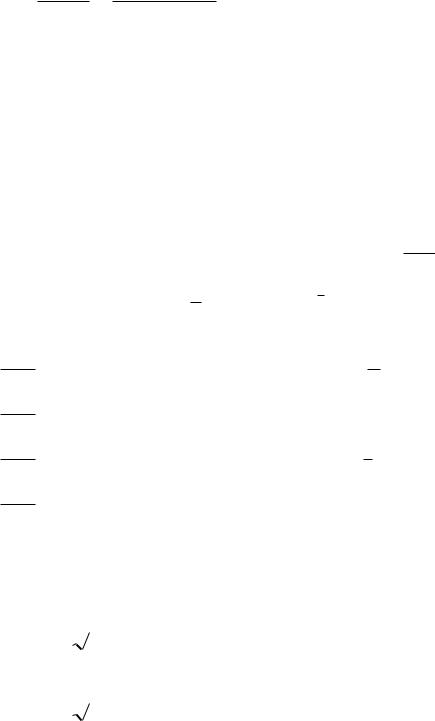
3)	lim
	x x
	0

f ( x ) g( x ) lim f ( x ) lim g( x )
x x	x x
0	0

4)	lim
	x x
	0

f ( x ) g( x ) lim f ( x ) lim g( x )
x x	0	x x	0

5)	lim
	x x
	0

f ( x )		lim f ( x )
		x x	0
g( x )		lim g( x )
		x x
			0

, если lim q( x ) 0

x x0

Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям.

Элементарными приемами раскрытия неопределенностей являются:

1)сокращение на множитель, создающий неопределенность;

2)деление числителя и знаменателя на старшую степень аргумента

(для отношения многочленов при х 3) применение эквивалентных

больших;

);

бесконечно малых и бесконечно

4) применение первого

замечательного предела lim x

замечательного предела

	1	x	1
1			lim 1 x x	e
	x		x

	lim	sin x	1
		x
	x 0

и второго

Кроме того, при вычислении пределов полезно запомнить следующее:

	lim	f ( x )
		( x )
	x a
	lim	f ( x )
		( x )
	x a
	lim	f ( x )
		( x )
	x a
	lim	f ( x )
		( x )
	x a

=0, если			lim f ( x
			x a
=		, если	lim f (
			x a
=0, если			lim f ( x
			x a
=		, если	lim f (
			x a

) c x ) ) 0 x )

, lim ( x ) ,			с
	т.е.						=0
x a
c ,lim ( x ) 0,			с
	т.е.				=
x a			0
, lim ( x ) с ,	0
	т.е.					=0
x a		с
, lim ( x ) с , т.е.								=
x a						с

Может также понадобится таблица бесконечно малых в окрестности х0 функций, эквивалентных данным.

tgmx ~ mx
sain mx ~ mx
3			~ 1 x
	x 1 1
					3
arctg mx ~ mx
						x				x 0
	x 1 1 ~								при
					2
1 cos 2 x ~						3 sin 2
									x
					2
arcsin mx ~ mx
				x 2
1 cos x ~
					2

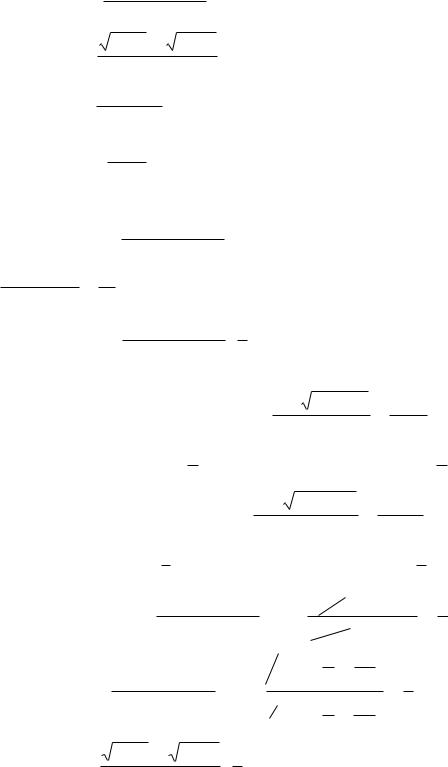
Практическая часть:

1. Найти пределы функций:

2x

2

5x 3

1) lim

приx

2; x

3; x

;

2

4x 15

0

0

0

x x 0 3x

2) lim

x 1

7 x

;

x 4

x 4

3) lim

1 cosx

;

3x sin x

x 0

x

3

x 2

4) lim

.

x x

1

Решение

1а)

8 10 3 12 8 15

1б)

				2x		2	5x 3
	lim
					2		4x 15
	x 2			3x
		5	.
		11
				2x		2	5x 3
	lim
					2		4x 15
	x 3			3x

=(так как функция непрерывна при х=2)=

	0
		.Разложим числитель и знаменатель на
	0

множители.

2x	2	5x	3 0;	x			5	25 24		5	7	;
					1,2			4		4

		x
		1
3x	2

3, x	2
4x 15

1

2

0;

. 2x
x	1,2

2	5x
4		16
		6

3

	2(x 3)(x				1	) (x 3)(2x	1).
					2
	180		4 14	;
			6

x			3, x							5	. 3x							2	4x 15 3(x									3)(x				5	) (x 3)(3x 5).
	1				2					3																						3
										2x			2			5x			3						(x 3)(2x 1)									1
Получим					lim																lim														.
												2
					x 3 3x											4x 15						x 3 (x 3)(3x 5)												2
																					x		2	(2		5		3		)
							2
				2x					5x						3											x		x	2		2
1в)			lim														lim														.
						2		4x						15									2			4		15
			x 3x																x			x		(3						)	3
																										x		x	2
2)		lim		x 1								7 x							0			(Домножим числитель и знаменатель на
							x 4
	x 4																		0

сумму корней)