Тема 2: Отношения, отображения, функции Лекции 2 - 3

Цель: рассмотреть понятия соответствия, отношения, отображения, функции, их отличия, свойства; проиллюстрировать основные понятия на примерах.

План:

1. Понятие кортежа

2 Декартово произведение множеств

3. Бинарные отношения во множествах

4. Способы задания отношений

5. Свойства отношений

6. Отношение эквивалентности

7. Отношение порядка

8. Отображения множеств.

9. Функции

Литература: 1. Москвинова Г. И. Дискретная математика. Математика для менеджера в примерах и упражнениях : учебное пособие / Г.И. Москвинова – М. : Логос, 2000. – 240 с.: ил.

1. Понятие кортежа

Пусть даны множества А₁, А₃, …A_n. Выберем из первого множества элемент a₁, из второго – а₂ и т.д. Из множества А_n выберем элемент а_n. Расположим элемен­ты в порядке их извлечения. Получим упорядоченную последовательность (a_1, а₂,.... a_n).

Опр: Упорядоченная последователь­ность (а₁, а₂...a_n) составленная из элементов множеств A₁,A₂…A_n, где a_iA_i , i=1,2…n, - называется кортежем длины n. Заметим, что множества A₁, A₂,… А_n могут иметь общие элемента или даже совпадать. Поэтому элементы в кортеже могут повторяться.

Опр: Два кортежа, составленные из элементов одного и того же множе­ства А считаются равными, если их длины равны и элементы сто­ящие на соответствующих мес­тах, равны т.е.

m=n,

(a₁,a₂,…a_m)=(b₁,b₂,…b_n) a_k=b_{k ,}

1 kn,

где a_iA, b_jA,

i=1,2,…m, j=1,2,…n.

Таким образом, когда мы говорим:

а) о кортеже, то

1) учитываем порядок расположения элементов;

2) элементы в кортеже могут повто­ряться.

б) о множестве, то

1)не учитываем порядок расположения элементов;

2)ни один элемент множества не должен повторятся.

Опр: Элементы a₁,a₂,…a_n кортеже (a₁,a₂,…a_n) называются его компонентами или координатами.

2 Декартово произведение множеств

Опр: Декартовым произведением множествa A₁,A₂,…A_n называется множество, эле­ментами которого являются все кортежи длины n, составленные из элементов этих множеств.

Декартово произведение обоз­начают

A₁A₂…A_n  (a₁,a₂,…a_n)a_kA_k,1kn

Пример

1) А=б,и,г;

В={а,д;

АВ=(б,а);(б,д);(и,а);(и,д);(г,а);(г,д).

Пример

А={1,2};

В=3,4,5;

АВ=(1,3);(1,4);(1,5);(2,3);(2,4);(2,5)};

ВА={(3,1);(4,1);(5,1);(3,2);(4,2);(5,2)};

АВ  ВА.

Декартово произведение множеств не коммутативно.

Пример

(АВ)СА(ВС).

Так как ((a,b),c)(a,(b,c)),

то декартово произведение множеств не ассоциативно.

Пример

Пусть А=В=R, где R - множество действительных чисел,

тогда AB=RR=R²=(a,b)a,bR, ( рисунок 10).Каждую пару (а,b) можно изобразить точкой М(а,b) на координатной плоско­сти (рисунок 10). Связь с декартовой системой коорди­нат и объясняет название "декартово произведение множеств".

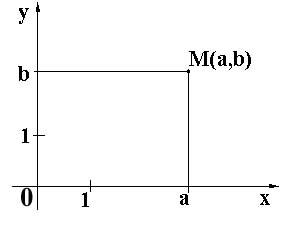
Рисунок –Декартово произведение множеств

Очевидно, что плоскость можно рас­сматривать как декартово произведение двух прямых линий (оси абсцисс и оси ординат) - каждая точка плоскости задаётся парой точек этих прямых.

Декартово произведение n элементов множества R называют n-мерным ариф­метическим пространством и обозначают Rⁿ= R R…R.

Пример

Пусть А и В - множества точек отрезков прямых (осей координат),

тогда АВ можно изобразить в виде множества точек прямоугольника (рисунок 11).

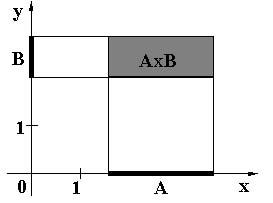
Рисунок –Декартово произведение множеств А и В

Пусть множества А и В конечны, при­чём А состоит из m элементов, а

В - из n элементов:

A={a₁,a₂,…a_m}; B={b₁,b₂,…b_n},

тогда АВ состоит из mn пар. Чтобы убедиться в этом, достаточно записать все пары, входящие в АВ в виде:

(a₁,b₁)…(a₁,b_n)

(a₂,b₁)…(a₂,b_n)

………………

(a_m,b₁)…(a_m,b_n)

Доказанное утверждение можно представить в виде равенства:

AB=AB,

где - число элементов множества А;

- число элементов множества В;

- число элементов декартова произведе­ния АВ.