ОИУСЗИ / MSZI_2003

Классификация криптографических методов 341

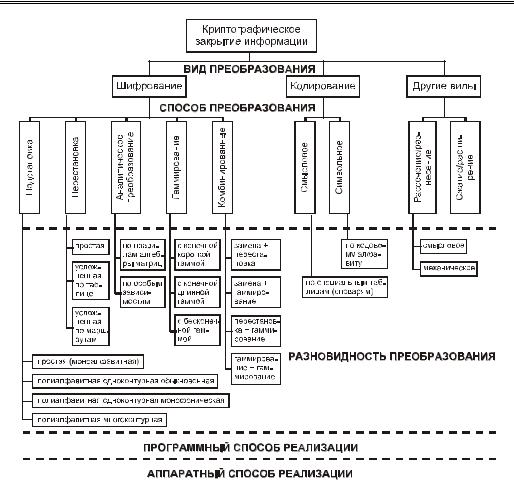
Под шифрованием в данном случае понимается такой вид криптографического закрытия, при котором преобразованию подвергается каждый символ защищаемого сообщения. Все известные способы шифрования разбиты на пять групп: подстановка (заме-

на), перестановка, аналитическое преобразование, гаммирование и комбинированное шифрование. Каждый из этих способов может иметь несколько разновидностей.

Под кодированием понимается такой вид криптографического закрытия, когда некоторые элементы защищаемых данных (не обязательно отдельные символы) заменяются заранее выбранными кодами (цифровыми, буквенными, буквенно-цифровыми сочетаниями и т.д.). Этот метод имеет две разновидности: смысловое и символьное кодирование. При смысловом кодировании кодируемые элементы имеют вполне определенный смысл (слова, предложения, группы предложений). При символьном кодировании кодируется каждый символ защищаемого текста. Символьное кодирование по существу совпадает с подстановочным шифрованием.

К отдельным видам криптографии относятся методы рассечения-разнесения и сжатия данных. Рассечение-разнесение заключается в том, что массив защищаемых данных делится (рассекается) на такие элементы, каждый из которых в отдельности не позволяет раскрыть содержание защищаемой информации. Выделенные таким образом элементы данных разносятся по разным зонам памяти или располагаются на разных носителях. Сжатие данных представляет собой замену часто встречающихся одинаковых строк данных или последовательностей одинаковых символов некоторыми заранее выбранными символами.

342 Глава 18. Криптографическая защита

Рис. 18.1. Классификация криптографических методов

Требования к криптографическим методам защиты информации

Раскрытие зашифрованных текстов (в первую очередь нахождение ключа) осуществляется при помощи методов криптоанализа. Основными методами криптоанализа являются:

•статистические, при которых зная статистические свойства открытого текста пытаются исследовать статистические закономерности шифротекста и на основании обнаруженных закономерностей раскрыть текст;

•метод вероятных слов, в котором при сопоставлении некоторой небольшой части шифротекста с известным фрагментом открытого текста пытаются найти ключ и с его помощью расшифровать весь текст. Требуемый фрагмент открытого текста можно найти с помощью статистических методов или просто угадать, исходя из предполагаемого содержания или структуры открытого текста.

Классификация криптографических методов 343

Поскольку криптографические методы ЗИ применяются давно, то уже сформулированы основные требования к ним.

1.Метод должен быть надежным, т.е. восстановление открытого текста при владении только шифротекстом, но не ключом должно быть практически невыполнимой задачей

2.Из-за трудности запоминания объем ключа не должен быть большим.

3.Из-за трудностей, связанных со сложными преобразованиями, процессы шифрования должны быть простыми.

4.Из-за возможности появления ошибок передачи дешифрование шифротекста, содержащего отдельные ошибки, не должно привести к бесконечному увеличению ошибок в полученном предполагаемом открытом тексте.

5.Из-за трудностей передачи объем шифротекста не должен быть значительно больше открытого текста.

Перечисленные требования были разработаны для традиционной криптографии. При современном развитии техники необходимость удовлетворения перечисленным

требованиям претерпевает существенные изменения.

В связи с развитием технологии, позволяющей с большой плотностью записать и длительное время надежно хранить большие объемы информации, условие небольшого объема ключа может быть ослаблено (по существу это условие, как и все остальные, приобретает новый смысл, соответствующий достигнутому уровню техники). В связи с развитием микроэлектроники появляется возможность разработки дешевых устройств, осуществляющих быстро и точно сравнительно сложные преобразования информации. С другой стороны, возможность увеличения скорости передачи отстает от возможности увеличения скорости обработки информации. Это, несомненно, позволяет ослабить требование п. 3 без ущерба для практически достигаемой скорости передачи. В настоящее время связное оборудование является высоконадежным, а методы обнаружения и исправления ошибок — хорошо развитыми. К тому же, обычно используемые в компьютерных сетях протоколы сеансов связи предусматривают передачу любого текста даже при наличии сбоев во время передачи. Поэтому требование п. 4 в значительной мере потеряло свою актуальность. В отдельных случаях, если каналы связи не перегружены, может быть ослаблено и требование п. 5.

Таким образом, не затронутым осталось требование п. 1, при рассмотрении которого следует учесть два обстоятельства.

Во-первых, в автоматизированных системах (АС) циркулируют большие объемы информации, а наличие большого объема шифротекста облегчает задачу криптоанализа.

Во-вторых, для решения задачи криптоанализа можно использовать ЭВМ. Это позволяет в новых условиях требовать значительного увеличения надежности. Другим важным отрицательным фактором применения криптографии в АС является то, что часто используются языки с весьма ограниченным запасом слов и строгим синтаксисом (языки программирования).

344Глава 18. Криптографическая защита

Всвязи с новыми специфическими применениями криптографических методов могут быть выдвинуты также другие требования. Так, например, второй важной областью применения криптографических методов ЗИ являются системы управления базами данных (СУБД). В этом случае к криптографическим методам ЗИ предъявляются следующие дополнительные требования.

1.Из-за невозможности чтения и возобновления записей с середины файла, шифрование и дешифрование каждой записи должны производиться независимо от других записей.

2.Для создания больших удобств обработки и во избежание излишней перегрузки системы вспомогательными преобразованиями необходимо все операции с файлами проводить с данными в зашифрованном виде.

Специфика СУБД оказывает влияние на надежность защиты по следующим причинам:

•данные в СУБД продолжительное время находятся в зашифрованном виде. Это затрудняет или даже делает невозможной частую смену ключей, и в связи с этим ЗИ становится менее надежной;

•ключи могут не передаваться по разным адресам, а храниться все в одном месте. Это повышает надежность системы из-за уменьшения возможности овладения ключами посторонними лицами.

Вфайловых системах вероятность появления ошибки гораздо меньше, чем в каналах связи, поэтому требование п. 4 для файловых систем не имеет большого практического значения.

Появление быстродействующих ЭВМ способствует возникновению так называемой вычислительной криптографии, тесно связанной с вычислительной техникой.

Математика разделения секрета

Рассмотрим следующую, в наше время вполне реальную ситуацию. Два совладельца драгоценности хотят положить ее на хранение в сейф. Сейф современный, с цифровым замком на 16 цифр. Так как совладельцы не доверяют друг другу, то они хотят закрыть сейф таким образом, чтобы они могли открыть его вместе, но никак не порознь. Для этого они приглашают третье лицо, называемое дилером, которому они оба доверяют (например, потому что оно не получит больше доступ к сейфу). Дилер случайно выбирает 16 цифр в качестве “ключа”, чтобы закрыть сейф, и затем сообщает первому совладельцу втайне от второго первые 8 цифр “ключа”, а второму совладельцу втайне от первого

— последние 8 цифр “ключа”. Такой способ представляется с точки здравого смысла оптимальным, ведь каждый из совладельцев, получив “полключа”, не сможет им воспользоваться без второй половины, а что может быть лучше?! Недостатком данного примера является то, что любой из совладельцев, оставшись наедине с сейфом, может за пару минут найти недостающие “полключа” с помощью несложного устройства, предназначенного для перебора ключей и работающего на тактовой частоте 1 МГц. Кажется, что единственный выход — в увеличении размера “ключа”, скажем, вдвое. Но есть другой

Математика разделения секрета 345

математический выход, опровергающий (в данном случае — к счастью) соображения здравого смысла. А именно, дилер независимо выбирает две случайные последовательности по 16 цифр в каждой, сообщает каждому из совладельцев втайне от другого “его” последовательность, а в качестве “ключа”, чтобы закрыть сейф, использует последовательность, полученную сложением по модулю 10 соответствующих цифр двух выбранных последовательностей. Довольно очевидно, что для каждого из совладельцев все 1016 возможных “ключей” одинаково вероятны и остается только перебирать их, что потребует в среднем около полутора лет для устройства перебора ключей, оборудованного процессором с частотой 100 МГц.

И с математической, и с практической точки зрения неинтересно останавливаться на случае двух участников и следует рассмотреть общую ситуацию. Неформально говоря, схема, разделяющая секрет (СРС) позволяет “распределить” секрет между n участниками таким образом, чтобы заранее заданные разрешенные множества участников могли однозначно восстановить секрет (совокупность этих множеств называется структурой доступа), а неразрешенные — не получали никакой дополнительной к имеющейся априорной информации о возможном значении секрета. СРС с последним свойством назы-

ваются совершенными.

История СРС начинается с 1979 года, когда эта проблема была поставлена и во многом решена Блейкли и Шамиром для случая пороговых (n, k)-СРС (т.е. разрешенными множествами являются любые множества из k или более элементов). Особый интерес вызвали так называемые идеальные СРС, т.е.такие, где объем информации, предоставляемой участнику, не больше объема секрета. Оказалось, что любой такой СРС соответствует матроид и, следовательно, не для любой структуры доступа возможно идеальное разделение секрета. С другой стороны, было показано, что для любого набора разрешенных множеств можно построить совершенную СРС, однако известные построения весьма неэкономны. Рассмотрим некоторые алгебро-геометрические и комбинаторные задачи, возникающие при математическом анализе СРС.

Будем говорить, что семейство подпространств {L0, …, Ln} конечномерного векторного пространства L над полем K удовлетворяет свойству “все или ничего”, если для любого множества A {1, …, n} линейная оболочка подпространств {La: a A} либо содержит подпространство L0 целиком, либо пересекается с ним только по вектору 0. В подразделе “Линейное разделение секрета” мы увидим, что такое семейство задает “линейную” СРС, у которой множество A {1, …, n} является разрешенным, если и только если линейная оболочка подпространств {La: a A} содержит подпространство L0 целиком. В связи с этим понятием возникает ряд вопросов. Например, если поле K конечно (|K| = q) и все подпространства {L0, …, Ln} одномерны, то каково максимально возможное число участников n для линейных пороговых (n, k)-СРС (k > 1)? Иначе говоря, каково максимально возможное число векторов {h0, …, hn} таких, что любые k векторов, содержащие вектор h0, линейно независимы, а любые k + 1 векторов, содержащие вектор h0, линейно зависимы. Оказывается, что это свойство эквивалентно следующему, на первый взгляд более сильному, свойству: любые k векторов линейно независимы, а любые k + 1 — линейно зависимы. Такие системы век-

346 Глава 18. Криптографическая защита

торов изучались в геометрии как N-множества (N = n + 1) в конечной проективной геометрии PG(k–1, q), в комбинаторике — как ортогональные таблицы силы k и индекса λ = 1, в теории кодирования — как проверочные матрицы МДР кодов. В подразделе “Линейное разделение секрета” мы приведем известную конструкцию таких множеств с N = q + 1. Существует довольно старая гипотеза о том, что это и есть максимально возможное N, за исключением двух случаев: случая q < k, когда N = k + 1,

и случая q = 2m, k = 3 или k = q – 1, когда N = q + 2.

Разделение секрета для произвольных структур доступа

Начнем с формальной математической модели. Имеется n+1 множество S0, S1, …, Sn и (совместное) распределение вероятностей P на их декартовом произведении S = S0 * …* Sn. Соответствующие случайные величины обозначаются через Si. Имеется также некоторое множество Г подмножеств множества {1, …, n}, называемое структурой доступа.

Определение 18.1

Пара (P,S) называется совершенной вероятностной СРС, реализующей структуру доступа Г, если

P(S0 = c0 | Si = ci, i A) {0, 1} для A Г,	(18.1)
P(S0 = c0 | Si = ci, i A) = P(S0 = c0) для A Г	(18.2)

Это определение можно истолковать следующим образом. Имеется множество S0 всех возможных секретов, из которого секрет s0 выбирается с вероятностью p(s0), и имеется СРС, которая “распределяет” секрет s0 между n участниками, посылая “проекции” s1, …, sn секрета с вероятностью PS0 (s1, …, sn). Отметим, что і-ый учасник получает свою “проекцию” si Si и не имеет информации о значениях других “проекций”, однако знает все множества Si, а также оба распределения вероятностей p(s0) и PS0(s1, …, sn). Эти два распределения могут быть эквивалентны заменене на одно: P(s0,

s1, …, sn) = p(S0)PS0(s1, …, sn), что и было сделано выше. Цель СРС, как указывалось во введении, состоит в том, чтобы:

•участники из разрешенного множества A (т. е. A Г) вместе могли бы однозначно восстановить значение секрета — это отражено в свойстве (18.1);

•участники, образующие неразрешенное множество А (А Г), не могли бы получить

дополнительную информацию об s0, т.е., чтобы вероятность того, что значение секрета S0 = c0, не зависела от значений “проекций” Si при і А — это свойство (18.2).

Замечание о терминологии. В англоязычной литературе для обозначения “порции” информации, посылаемой участнику СРС, были введены термины share (А. Шамир) и shadow (Г. Блейкли). Первый термин оказался наиболее популярным, но неадекватная (во всех смыслах) замена в данной работе акции на проекцию может быть несколько оправдана следующим примером.

Математика разделения секрета 347

Пример 18.1. Множество S0 всех возможных секретов состоит из 0, 1 и 2, “представленных”, соответственно: шаром; кубом, ребра которого параллельны осям координат; цилиндром, образующие которого параллельны оси Z. При этом диаметры шара и основания цилиндра, и длины ребра куба и образующей цилиндра, равны. Первый участник получает в качестве своей “доли” секрета его проекцию на плоскость XY, а второй — на плоскость XZ. Ясно, что вместе они однозначно восстановят секрет, а порознь — нет. Однако эта СРС не является совершенной, так как любой из участников получает информацию о секрете, оставляя только два значения секрета как возможные при данной проекции (например, если проекция — квадрат, то шар невозможен).

Еще одно замечание. Элемент (участник) x {1, …, n} называется несущественным (относительно Г), если для любого неразрешенного множества А множество А x также неразрешенное. Очевидно, что несущественные участники настолько несущественны для разделения секрета, что им просто не нужно посылать никакой информации. Поэтому далее, без ограничения общности, рассматриваются только такие структуры доступа Г, для которых все элементы являются существенными. Кроме того, естественно предполагать, что Гявляется монотонной структурой, т.е. из А В, А Гследует В Г.

Пример 18.2. Рассмотрим простейшую структуру доступа — (n,n)-пороговую схему, т.е. все участники вместе могут восстановить секрет, а любое подмножество участников не может получить дополнительной информации о секрете. Будем строить идеальную СРС, выбирая и секрет, и его проекции из группы Zq вычетов по модулю q, т.е. S0 = S1 = … = Sn = Zq. Дилер генерирует n–1 независимых равномерно распределенных на Zq случайных величин хi и посылает і-му учаснику (і = 1, ... , n-1) его “проекцию” si = xi, а n-му участнику — sn = s0 – (s1 + … + sn-1). Кажущееся “неравноправие” n-ого участника тут же исчезает, если мы выпишем распределение PS0(s1,…, sn), которое очевидно равно 1/qn–1, если s0 = s1 + … + sn, а в остальных случаях равно 0. Теперь легко проверяется и свойство (18.2), означающее в данном случае независимость случайной величины S0 от случайных величин {Si: і А} при любом собственном подмножестве А.

Данное выше определение СРС, оперирующее понятием распределение вероятностей, ниже переведено, почти без потери общности, на комбинаторный язык, который представляется более простым для понимания. Произвольная M * (n + 1)-матрица V, строки которой имеют вид v = (v0, v1, …, vn), где vi Si, называется матрицей комби-

наторной СРС, а ее строки — правилами распределения секрета. Для заданного значе-

ния секрета s0 дилер СРС случайно и равновероятно выбирает строку v из тех строк матрицы V, для которых значение нулевой координаты равно s0.

Определение 18.2

Матрица V задает совершенную комбинаторную СРС, реализующую структуру доступа Г, если, во-первых, для любого множества А Г нулевая координата любой строки матрицы V однозначно определяется значениями ее координат из множества А, и, вовторых, для любого множества А Г и любых заданных значений координат из множества А число строк матрицы V с данным значением α нулевой координаты не зависит от

α.

348 Глава 18. Криптографическая защита

Сопоставим совершенной вероятностной СРС, задаваемой парой (P, S), матрицу V, состоящую из строк s S, таких что P(s) > 0. Заметим, что если в определении 1 положить все ненулевые значения P одинаковыми, а условия (18.1) и (18.2) переформулировать на комбинаторном языке, то получится определение 2. Это комбинаторное определение несколько обобщается, если допустить в матрице V повторяющиеся строки, что эквивалентно вероятностному определению 1, когда значения вероятностей P(s) — рациональные числа.

Продолжение примера 18.2 (из предыдущего раздела). Переформулируем данную выше конструкцию (n,n)-пороговой СРС на комбинаторном языке. Строками матрицы V являются все векторы s такие, что s0 + s1 + … + sn = 0. Очевидно, что матрица V задает совершенную комбинаторную СРС для Г={1, …, n}, так как для любого собственного подмножества А {1, …, n} и любых заданных значений координат из множества А число строк матрицы V с данным значением нулевой координаты равно qn–1 – |A|.

Удивительно, но простой схемы примера 2 оказывается достаточно, чтобы из нее, как из кирпичиков, построить совершенную СРС для произвольной структуры доступа. А именно, для всех разрешенных множеств, т.е. для А Г, независимо реализуем описанную только что пороговую (|A|, |A|)-СРС, послав тем самым і-му учаснику cтолько “проекций” siA, скольким разрешенным множествам он принадлежит. Это словесное описание несложно перевести на комбинаторный язык свойств матрицы V и убедиться, что эта СРС совершенна. Как это часто бывает, “совершенная” не значит “экономная”, и у данной СРС размер “проекции” оказывается, как правило, во много раз больше, чем размер секрета. Эту схему можно сделать более экономной, так как достаточно реализовать пороговые (|A|, |A|)-СРС только для минимальных разрешенных множеств А, т.е. для А Гmin, где Гmin — совокупность минимальных (относительно включения) множеств из Г. Тем не менее, для пороговой (n, n/2)-СРС размер “проекции” (измеренный, например, в битах) будет в Cnn/2 ~ 2n/ 2πn раз больше размера секрета (это наихудший случай для рассматриваемой конструкции). С другой стороны, как мы убедимся чуть позже, любая пороговая структура доступа может быть реализована идеально, т.е. при совпадающих размерах “проекции” и секрета. Поэтому естественно возникает вопрос о том, каково максимально возможное превышение размера “проекции” над размером секрета для наихудшей структуры доступа при наилучшей реализации. Формально, R(n) = max R(Г), где max берется по всем структурам доступа Г на n участниках, а R(Г) =

min max log |Si| , где min берется по всем СРС, реализующим данную структуру доступа

log |S0|

Г, а max — по і = 1, ..., n. Приведенная конструкция показывает, что R(n) ≤ Cnn/2n. С другой стороны, R(n) ≥ n/log n. Такой огромный “зазор” между верхней и нижней оценкой дает достаточный простор для исследований (предполагается, что R(n) зависит от n экспоненциально).

Линейное разделение секрета

Начнем с предложенной Шамиром элегантной схемы разделения секрета для пороговых структур доступа. Пусть К = GF(q) — конечное поле из q элементов (например, q = p — простое число и К = Zp) и q > n. Сопоставим участникам n различных ненуле-

Математика разделения секрета 349

вых элементов поля {a1, …, an} и положим a0 = 0. При распределении секрета s0 дилер СРС генерирует k–1 независимых равномерно распределенных на GF(q) случайных величин fj (j = 1, …, k–1) и посылает і-му учаснику (і = 1, ..., n) “его” значение si = f(ai) многочлена f(x) = f0 + f1x + … + fk-1xk-1, где f0 = s0. Поскольку любой многочлен степени k-1 однозначно восстанавливается по его значениям в произвольных k точках (например, по интерполяционной формуле Лагранжа), то любые k участников вместе могут восстановить многочлен f(x) и, следовательно, найти значение секрета как s0 = f(0). По этой же причине для любых k–1 участников, любых полученных ими значений проекций si и любого значения секрета s0 существует ровно один “соответствующий” им многочлен, т.е. такой, что si = f(ai) и s0 = f(0). Следовательно, эта схема является совершенной в соответствии с определением 2. “Линейность” данной схемы становится ясна, если записать “разделение секрета” в векторно-матричном виде:

s = fH,

(18.3)

где s = (s0, …, sn), f = (f0, …, fk–1), k × (n+1) — матрица H = (hij) = (aij-1) и h00 = 1.

Заметим, что любые k столбцов этой матрицы линейно независимы, а максимально возможное число столбцов матрицы H равно q, чтобы добиться обещанного значения q+1 надо добавить столбец, соответствующий точке “бесконечность”.

Возьмем в (18.3) в качестве H произвольную r × (n + 1)-матрицу с элементами из поля K. Получаемую СРС, будем называть одномерной линейной СРС. Она является совершенной комбинаторной СРС со структурой доступа Г, состоящей из множеств А таких, что вектор h0 представим в виде линейной комбинации векторов {hj: j A}, где hj

— это j-ый столбец матрицы H. Строками матрицы V, соответствующей данной СРС, являются, как видно из (18.3), линейные комбинации строк матрицы H. Перепишем (18.3) в следующем виде

sj = (f, hj) для j = 0, 1, …, n,

где (f, hj) — скалярное произведение векторов f и hj. Если А Г, т.е. если h0 =

Σλjhj, то

s0 = (f, h0) = (f, Σλjhj) = Σλj(f, hj) = Σλjsj

и, следовательно, значение секрета однозначно находится по его “проекциям”. Рассмотрим теперь случай, когда вектор h0 не представим в виде линейной комбинации векторов {hj: j A}. Нам нужно показать, что в этом случае для любых заданных значений координат из множества А число строк матрицы V с данным значением любой координаты не зависит от этого значения. В этом не трудно убедится, рассмотрев (18.3) как систему линейных уравнений относительно неизвестных fi и воспользовавшись тем, что система совместна тогда и только тогда, когда ранг матрицы коэффициентов равен рангу расширенной матрицы, а число решений у совместных систем одинаково и равно числу решений однородной системы.

Указание. Рассмотрите две системы: c “нулевым” уравнением и без него (т.е. со свободным членом). Так как вектор h0 не представим в виде линейной комбинации векто-

350 Глава 18. Криптографическая защита

ров {hj: j A}, то ранг матрицы коэффициентов второй системы на 1 больше ранга матрицы коэффициентов первой системы. Отсюда немедленно следует, что если первая система совместна, то совместна и вторая при любом s0.

Эта конструкция подводит нас к определению общей линейной СРС. Пусть секрет и его “проекции” представляются как конечномерные векторы si = (s1i, …, smi i) и генерируются по формуле si = fHi, где Hi — некоторые r × mi-матрицы. Сопоставим каждой матрице Hi линейное пространство Li ее столбцов (т.е. состоящее из всех линейных комбинаций вектор-столбцов матрицы Hi). Несложные рассуждения, аналогичные приведенным выше для одномерного случая (все mi = 1), показывают, что данная конструкция дает совершенную СРС тогда и только тогда, когда семейство линейных подпространств {L0, …, Ln} конечномерного векторного пространства Kr удовлетворяет упомянутому выше свойству “все или ничего”. При этом множество А является разрешенным {La: a A} содержит подпространство L0 целиком. С другой стороны, множество А является неразрешенным (А Г), если и только если линейная оболочка подпространств {La: a A} пересекается с подпространством L0 только по вектору 0. Отметим, что если бы для некоторого А пересечение L0 и линейной оболочки {La: a A} было нетривиальным, то участники А не могли бы восстановить секрет однозначно, но получали бы некоторую информацию о нем, т.е. схема не была бы совершенной.

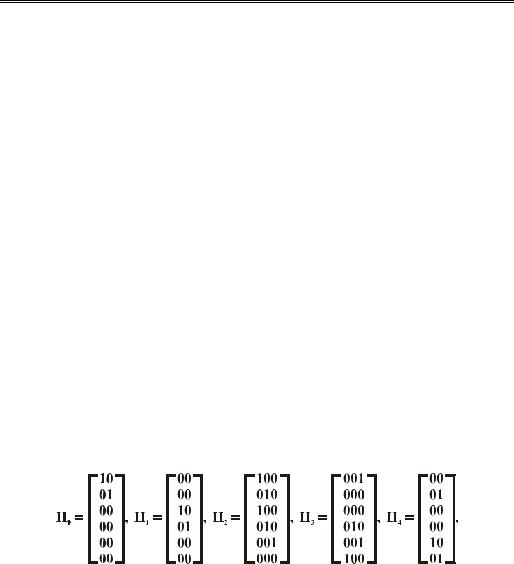
Пример 18.3. Рассмотрим следующую структуру доступа для случая четырех участников, задаваемую Гmin = {{1,2}, {2,3}, {3,4}}. Она известна как первый построенный пример структуры доступа, для которой не существует идеальной реализации. Более того, было доказано, что для любой ее совершенной реализации R(Г) ≥ 3/2. С другой стороны, непосредственная проверка показывает, что выбор матриц H0, H1, ..., H4, приведенных на рис. 18.2, дает совершенную линейную СРС с R = 3/2, реализующую эту структуру, которая, следовательно, является и оптимальной (наиболее экономной) СРС.

Рис. 18.2. Матрицы, реализующие совершенную линейную СРС

Идеальное разделение секрета и матроиды

Начнем с определения идеальных СРС. Для этого вернемся к комбинаторному определению совершенной СРС. Следующее определение совершенной СРС является даже более общим, чем вероятностное определение 1, поскольку условие (18.2) заменено в нем на более слабое.

Для произвольного множества В {0, 1, …, n} обозначим через VB M × |B|- матрицу, полученную из матрицы V удалением столбцов, номера которых не принадлежат множеству В. Пусть ||W|| обозначает число различных строк в матрице W.