10

Лекция № 6

Функция распределения случайной величины. Её свойства

Ряд распределения может быть построен только для дискретной случайной величины, Для непрерывной случайной величины ряд и многоугольник распределения не может быть построен, так как множество возможных значений такой величины несчётно. Наиболее общей формой закона распределения, пригодной для всех случайных величин (дискретных и непрерывных) является функция распределения.

Определение. Функцией распределения случайной величины Х называется функция F(х), заданная на всей числовой оси и представляющая собой вероятность того, что случайная величина примет значение меньшее, чем заданное х:

F( х ) = Р( Х<х ), хÎ(+ ¥, -¥ ) (1)

Геометрически функция распределения ( ф.р. ) интерпретируется как вероятность того, что случайная точка Х попадает левее заданной точки х ( на рис.1 соответствующая часть оси абсцисс, т.е. множество точек, представляющее событие {X<x} , отмечена штриховкой ).

Х<x

х

0 х

Рис.1

Свойства функции распределения

1). F(x)³0 . Сразу следует из определения .

2). F(x) - неубывающая функция своего аргумента , т.е. при х₁<x₂ F(x₁)£F(x₂) .

Доказательство: Рассмотрим на оси абсцисс две точки х₁ и х₂ , причём х₂>x₁ .

А В

0 x₁ x₂ x

C

Рис.2

Представим событие С={X<x₂} как сумму двух несовместных событий: С=А+B, где

А={X<x₁}, B={x₁£X<x₂}

По теореме сложения :

Р(С)=Р(А)+Р(В) ,т.е.

Р{Х<x₂}= P{X<x₁} + P{x₁£X<x₂}, или

F(x₂)= F(x₁) + P{x₁£X<x₂}, или

P{x₁£X<x₂}= F(x₂) - F(x₁)

Но Р{x₁£X<x₂} как всякая вероятность не может быть отрицательной, следовательно, F(x₂)³F(x₁) ˜

3). P(a£X<b) = F(b) - F(a)

Доказательство: Представим случайное событие в виде :

{X<b} = {X<a} + {a£X<b}

P{X<b} = P{X<a} + P{a£X<b}

Т.к. по определению:

P{X<a}=F(a) и P{X<b}=F(b), то

P{a£X<b} = F(b) - F(a)

т.е. вероятность того , что случайная величина Х в результате опыта попадёт на участок [a,b), включая а равна приращению функции распределения на этом участке. ‚

4) . F(x) непрерывна слева

Доказательство. Выберем какую-нибудь возрастающую последовательность значений х₁<x₂<...<x_n<..., сходящуюся к х₀, т.е. х_n®x_0. Обозначим через А_n событие {x_n£X£x₀},т.е. А_n={x_n £ X £ x₀}. Ясно, что А_i Ì A_j , при i>j и произведение всех событий A_n есть невозможное событие - Æ. По аксиоме непрерывности при n ®¥ должно быть lim P (A _n) =P (Æ) =0. С другой стороны

–

5). ,

Доказательство: Рассмотрим случайное событие {X<x}®{X<-¥}= Æ, x®-¥ это событие невозможное P{X<x}®P{Æ}=0, x®-¥, отсюда

Далее {X<x}®{X<+¥}=W - достоверное событие

^x®+¥

P{X<x}®P{W}=1, или по определению

^x®+¥



Итак, функция распределения F(x) любой случайной величины есть неубывающая функция своего аргумента, значения которой заключены между 0 и 1: 0£F(x)£1, причём F(+¥)=1, F(-¥)=0. В отдельных случаях эта функция может иметь скачки (разрыв первого рода), на некоторых участках она может быть постоянной, на других монотонно возрастать (см. рис.3) Зная функцию распределения случайной величины Х, можно вычислять вероятности любых событий.

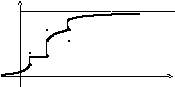F(x)

1

0 x

Рис.3. Вид функции распределения.

6). Функция распределения (ф.р.) может иметь не более, чем счётное число скачков.

Скачком ф.р. в точке х₀ называется разность F(x₀)-F(x₀-0)=C₀>0, C₀< ¥. Здесь х₀ - точка разрыва

7). Функция распределения дискретной с.в. меняется скачком на величину р_i в точках всевозможных значений с.в. Х=х_i, и остаётся постоянной вне этих точек.

Итак, видим, что каждая функция распределения F(x) является неубывающей, непрерывной слева и удовлетворяющей условию F(-¥)=0 и F(+¥)=1; 0£F(x)£1 функцией. Верно и обратное: каждая функция, удовлетворяющая перечисленным условиям может рассматриваться как функция распределения некоторой случайной величины.