8

ЛЕКЦИЯ № 7

Непрерывная случайная величина. Плотность распределения

Пусть дискретная случайная величина Х имеет много возможных значений, расположенных близко друг к другу на числовой оси. Построим функцию распределения F(x). По мере увеличения числа значений случайной величины и уменьшения интервалов между ними, число скачков становится все больше, а сами скачки все меньше. Ступенчатая линия функции распределения F(x) приближается к плавной непрерывной. Идеализацией является случай, когда функция F(x) непрерывна.

Определение Случайную величину Х назовем непрерывной, если ее функция распределения не только непрерывна в любой точке, но и дифференцируема всюду, кроме тех точек, где она терпит излом.

Так как для таких случайных величин функция F(x) нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю P{X=}=0 для любого  .

Для непрерывной случайной величины бессмысленно говорить о распределении вероятности между ее значениями. Для непрерывной случайной величины имеет смысл плотность распределения или плотность вероятности.

Используя механическую интерпретацию распределения вероятностей для дискретных случайных величин, представим, что масса, равная единице, не сосредоточена в отдельных точках, а непрерывно “размазана” по оси абсцисс Ох с какой-то неравномерной плотностью. Вероятность попадания случайной величины Х на любой участок х будет интерпретироваться как масса, приходящаяся на этот участок. Средняя плотность на этом участке рассматривается как отношение массы к длине. На участке [x, x+х) средняя плотность будет равна: P{xX x+х}/ х. Вероятность попадания случайной величины Х на участок [x, x+х) равна приращению функции распределения на этом участке; поэтому средняя плотность на участке от х до x+х будет равна

Переходя к пределу при х0, получим плотность в точке х

(1)

а это производная функции распределения.

Плотностью распределения (или плотностью вероятности, или плотностью) непрерывной случайной величины Х в точке х называется производная ее функции распределения в этой точке. Обозначение - f(x)

(2)

Про случайную величину Х говорят, что она распределена с плотностью f(x); имеет распределение с плотностью f(x). f(x) существует только для непрерывных случайных величин.

График плотности распределения f(x) называется кривой распределения. Рассмотрим непрерывную случайную величину Х с плотностью f(x) и элементарный участок dx, примыкающий к точке х (рис.1)

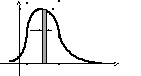f(x) f(x)

dx f(x)

x

0 x 0 a b x

Рис.1. Рис.2.

x

0 x

Рис.3.

Вероятность попадания случайной величины Х на участок dx равна f(x)dx. Эта величина называется элементом вероятности для точки х. Геометрически элемент вероятности приближенно равен площади элементарного прямоугольника, опирающегося на отрезок dx. Очевидно, что вероятность попадания случайной величины на участок (a,b) равна сумме элементов вероятности на всем этом участке, т.е. интегралу

(3)

т.е. эта вероятность равна площади, ограниченной сверху кривой распределения и опирающейся на участок (a,b) [заштрихована на Рис.2.]

Формула (3) дает возможность выразить функцию распределения F(x) через плотность распределения f(x)

(4)

В геометрической интерпретации функция распределения равна площади, ограниченной сверху кривой распределения и лежащей левее точки х (на Рис.3. эта площадь заштрихована)

Основные свойства плотности распределения

1. Плотность распределения - неотрицательная функция.

f(x)³0 (5)

Это свойство следует из определения f(x): производная неубывающей функции

отрицательной быть не может.

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

(условие нормировки)

(6)

Это свойство следует из формулы (4), если положить в ней x=¥ и учесть, что F(+¥)=1. Геометрически эти свойства плотности f(x) интерпретируются так:

1) вся кривая распределения лежит не ниже оси абсцисс;

2. полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.