Ledeneva_T_M_Algoritmy_teorii_grafov_Kodovye

61

структурой. К таким об ъектам, в частности, относятся территориально распределенные системы: информационные, транспортные, энергетические и т.п. Х орош им описанием различных коммуникационных сетей служит взвеш енный граф, реб рам и верш инам которого приписываю т веса, означаю щ иесоответственно пропускныеспособ ности линий связи и потреб ности(производственныемощ ности) об ъектов. Д лятакихвзвеш енныхграфов формулирую тсязадачидвухтипов:

а) оптимизировать значениефункционалов, заданныхнаэтихграфах;

б) синтезировать такиевесанареб рах графа, которыеоб еспечиваю т достижениеэкстремумафункционала, заданного намножествереб ер этого графа.

В математической постановке многие из подоб ных задач удается сформулировать в терминах линейного программирования. О днако оказывается, что удоб нееформулировать задачи линейного программированияв терминах распределенияпотоков награфах. Э то об ъясняетсятем, что для потоковых задач б ольш ой размерности в настоящ еевремяразраб отаны алгоритмы свысокойвычислительнойэффективностью .

Рассмотрим примеры потоковыхзадач.

Задач а о крат ч айшем пут и заклю чаетсяв нахождении пути минимальной длины отзаданной верш ины s к заданной верш инеt в ориентированном графе. Е слиграф являетсявзвеш енным, то под д ли ной пути подразумеваетсясуммадлиндуг, которыеэтотпуть составляю т; иначедлинапути - это количество дуг, об разую щ их этот путь. О б об щ ениями задачи о кратчайш ем путиявляю тся:

а) задачанахождениякратчайш ихпутеймежду верш иной s и всеми другими верш инамиграфа;

б) задачанахождениякратчайш ихпутеймежду всемипарамиверш ин. Е слиопределить кратчайш иепутиотзаданнойверш ины s ко всем ос-

тальным верш инам графа, то можно построить дерево кратчайш их путей. П ри реш ении задачи о кратчайш ем пути во взвеш енном графеследуетрассматривать три случая: а) вседуги имею тнеотрицательный вес; б ) некоторыедуги имею тотрицательный вес, но в графенесущ ествуетконтуров с суммарным отрицательным весом; в) в сети присутствует один или несколько контуров сотрицательным суммарным весом. В последнем случае задачу о кратчайш ем пути реш ить нельзя, но можно об наружить контуры с отрицательным суммарным весом. В случаеа) дляпоискакратчайш его пути между заданными верш инами используетсяалгоритм Д ейкстры; дляопределния кратчайш его пути с заданным числом дуг - алгоритм Ф ордаБеллмана; дляпоискакратчайш ихпутеймежду заданнойверш инойs ивсеми остальными можетб ыть использванкак алгоритм Д ейкстры, так и его модификации [2]. В случаях б ) и в) используется алгоритм Ф орда-М ура. Д ляопределениякратчайш его путимежду всемипарамиверш инприменим алгоритм Ф лойда[1]. Рассмотрим этиалгоритмы.

62

Алгор ит м Д ЕЙ К С ТРЫ

Ш аг 1 (присвоениеначальныхзначений). G - данныйграф, s - начальнаяверш инапути, t - конечнаяверш инапути. П оложить l(x)=0 дляx=s и считать эту пометку постоянной. П оложить l(xi) = ¥ длях¹s и считать эти пометкивременными. П оложить р=s.

Ш аг 2 (об новлениепометок). Д лявсеххiÎГ (р), пометки которыхвременные, изменить пометкив соответствиисправилом

l(xi)=min{ l(xi), l(p)+c(p, xi)}.

Ш аг 3 (превращ ение пометок в постоянные). Среди всех верш инс временными пометками найти такую xi*, для которой l(xi*)=min{ l(xi)}. Считать эту пометку верш ины xi* постояннойиположить р=xi*.

Ш аг 4. Е сли р¹t, то перейти к ш	агу 2. Е сли р=t, то l(p) - длинакрат-
чайш его пути. Ч тоб ы найти сам путь,	надо поступить следую щ им об разом:

положить y=t; из всехверш инxiÎГ -1(у) выделить такую верш ину х, длякоторой выполняется соотнош ение l(y)=l(x)+c(x,y); затем в качестве у рассматриваетсянайденнаяверш инахпроцесспродолжаетсядо техпор, пока неб удетдостигнутаверш инаs , тогдапуть из дуг, соединяю щ ихвыделенныеверш ины - искомыйкратчайш ийпуть из s в t. О станов.

Замечание. Различнаяинтерпретациявесов графаприводитк различным задачам, которыесводятсяк задачео кратчайш ем пути:

1. Наиболее н адеж н ы й пут ь. П усть весдуги представляетеенадежность, тогданадежность путиотs к t задаетсяформулой

(P) ∏rijr, =

i j P ) x, (x

гдеrij - надежность дуги(xi, xj), P - путь из s в t, содержащ ийдуги(xi, xj). Задачу нахождениянаиб олеенадежного пути отs к t можно свестик

задачео кратчайш ем путииз s в t, взяв в качествевесаcij дуги (xi, xj) внличину cij = -log rij, тогдаполучим

ρ( ) = å	ρij = −	åcij .		log	P	log
P ) x, (x		j	) x, (x	i j
			i
О тсю давидно, что кратчайш ий путь отs к t сматрицей весов {cij} б удетв
то жевремяинаиб олеенадежным путем сматрицей{rij}, анадежность это-
го путиравнаантилогарифму его длины.
2. Пут ь с н аибольш ей пр опуск н ой способн ост ью . В				этой задачекаж-
даядугаграфа(xi, xj) имеетпропускную	способ ность qij			и треб уетсянайти
путь отs к t снаиб ольш ей пропускной способ ностью . П ропускнаяспособ -
ность пути P определяетсядугой из P снаименьш ейпропускной способ но-
стью , т.е.	{qij }.	min
Q(P) =
i j	P ) x, (x

Сущ ествую ти другиепостановки задач, приводимыек задачео кратчайш ем пути.

63

В частном случае, если весавсехдуг равны 1, то длинапути есть количество дуг, которыесоставляю тэтотпуть. Д ляего определенияцелесооб разно использовать специальныйалгоритм – алгор ит м “ фр он т а волн ы ”:

	Ш	аг 1. G - данныйграф, s - начальнаяверш инапути, t - конечнаявер-
ш инапути. В ерш инеs приписать пометку 0. П оложить А ={s}, k=0.
	Ш	аг 2. Н айти множество Г (А ), положить k=k+1. В ерш инам, принад-
лежащ им множеству Г (А ), приписать пометки, равныеk.
	Ш	аг 3. Е сли верш ина t получила пометку, то перейти к ш агу
4,	иначе положить А = Г (А ) иперейтик ш агу 2.
Ш	аг 4.	П усть верш инаt имеетпометку l , тогдаl - длинапути сминималь-

ным числом дуг. Ч тоб ы найтипуть надо поступить следую щ им об разом: среди верш ин, смежных сt, найтитакую , у которой пометкаравна(l - 1), пусть это верш инаx. Затем среди верш ин, из которых ведут дуги в х, найтитакую , у которой пометка равна(l-2) ит. д. - процесспродолжается до техпор, поканеб удетдостигнутаверш ина s. П уть [s , ... , x , t] - искомый. О станов.

Е сли в сети некоторыедуги имею тотрицательный вес, то, как отмечалось выш е, алгоритм Д ейкстры не применим и используется алгор ит м Ф ор да-М ур а:

Замечание: А лгоритм основаннаприписывании верш инам пометок. lk(xi) - пометкаверш ины xi после(k+i) - той итерации. В результатераб оты алгоритмалиб о выдаетсясооб щ ениео сущ ествованиициклаотрицательного веса, либ о б удутопределены кратчайш иепутииз заданнойверш ины s во всеостальныеверш ины. П утиопределяю тсянаосновепометок так же, как

валгоритмеД ейсктры.

Шаг 1. П оложить S=Г (s), k=1; l1(s)=0 ; l1(xij)=C(s,xi) длявсех xiÎГ (s); l1(xi) = ¥ длявсехостальныхxi .

Ш аг 2. Д лякаждойверш ины xi Î Г (S) изменить пометки по прави-

лу:

lk+1(xi) = min{lk(xi),min{lk(xj)+c(xj,xi)}}, гдеxjÎTi =Г -1(xi)Ç S

Длявсехверш инxiÏГ (S) положить lk+1(xi)=lk(xi).

Шаг 3. Е сли k £ -1 и lk+1(xi) = lk(xi) и надвух предыдущ ихитерациях

пометкисовпадаю тдлявсехxi, то по полученным пометкам можно определить кратчайш иепути отзаданной точки s ко всем остальным верш инам. О станов. Е слиk<n-1 и lk+1(xi) ¹ lk(xi) длянекоторыхxi, то перейтик ш агу 4. Е сли k = n-1 и lk+1(xi) ¹ lk(xi) длянекоторыхxi, то в графесущ ествуетцикл отрицательного весаи задачанеимеетреш ения (сооб щ ениеоб ош иб ке и останов).

Шаг 4. П оложить S = {xi | lk+1(xi) ¹ lk(xi)}

Шаг 5. П оложить k = k+1 перейтик ш агу 2.

Задач а о крит ич еском пут иотличаетсяотзадачио кратчайш ем пути тем, что ищ етсяпуть максимальной длины. Заметим, что если весадуг неотрицательны, то можно использовать алгоритм Д ейкстры ссоответствую - щ имиизменениями, но сущ ествую тиспециальныеалгоритмы (одиниз них

64

приведенниже). М аксимальныйпуть иначеназываю ткритическим, ив сетевыхмоделяхониспользуетсядляреш ениясразу двухзадач – определения раннихвременнаступлениясоб ытий и дляосущ ествлениятопологической сортировкиверш инграфа– такойнумерацииверш ин, называемойправильной, когдадлякаждойдугиграфаномер начальнойверш ины меньш еномераконечной. Д ругоеееприменение– разложениеграфапо уровням, когда граф представляетсяв видеиерархическойструктуры, икаждаядугасоединяетверш ины только разных уровней. У ровни графаб ез контуров использую тсядляпостроенияпорядковой функции, лежащ ей в основенекоторых процедур классификации.

Д ляпроизвольного графаможно использовать алгор ит м пост р оен ия м ак сим альн огопут и с пом ощ ью базисн огодер ева:

Ш аг 1. Д ляданного орграфаG определить произвольноедерево скорнем в верш ине хо (хо - миноранта). М ножество дуг графаразб ить надва подмножестванаветвидерева(D ) ихорды (AD).

Ш	аг 2. К аждойверш инеграфахi Х поставить в соответствиеиндекс-
число,	равное длине пути от верш ины хо до верш ины хi . И ндекс первой

верш ины полагаем равным 0. И ндексы остальных верш инопределяю тся следую щ им об разом: отвыб ранной верш ины ищ ем путь до хо, идятолько по дугам деревапротив стрелок. Т акойпуть сущ ествуетиединствен. О дновременно складываем весасоответствую щ их дуг и получаем величину индексавыб раннойверш ины. И ндексы помещ аю тсяв массив IND.

Шаг 3. П оложить R=0. (R - признак измененияиндексов).

Шаг 4. П росматриваяхорды графав произвольном порядке, находим такие, весакоторыхувеличиваю тиндексы верш ин. П риэтом рассматриваемаяхордаиз AD переходитв D наместо удаляемойветви дерева; одновре-

менно из D удаляется таветвь, которая имеетодинаковую конечную вер- ш ину схордойиз AD. Н аосвоб ожденноеместо в массивеAD переходитдуга, удаленная из D. Д ругими словами, при увеличении индексов верш ин происходитоб мендугамимассивов D иAD. П риэтом положить R=1.

Ш	аг 5. Е сли вседуги AD просмотрены, то перейти к ш агу 6, иначе
перейтик ш агу 4.
Ш	аг 6. Е сли R=0, то перейтик ш агу 7, иначеперейтик ш агу 3.
Ш	аг 7. Д линамаксимального пути - индексконечной верш ины пути.

Ч тоб ы найтимаксимальныйпуть, достаточно идтипротив стрелок по дугам массиваD.

Е сли награф накладываю тсяограничения, то необ ходимо использовать специальныеалгоритмы. Т ак в задачахсетевого планированияорграф недолженсодержать контуров. В этом случаедля поискамаксимального пути, который называетсякрит ич еским , используетсяалгор ит м пост р ое-

н ия м ак сим альн ого(к р ит ического) пут и в ацик лическ ом взвеш ен н ом ор гр а-

фе:

Ш аг 1. (X,U) - данныйграф сматрицейвесов С. В ыполнить топологическую сортировку верш инграфа, при этом начальная верш инаполучает номер 1, аконечнаяномер n. (n=|X|.)

65

Шаг 2. Н ачальнойверш инеприсвоить пометку l(1)=0. П оложить k=1 ( k - номер рассматриваемойверш ины).

Шаг 3. Е сли всеверш ины помечены, то перейти к ш агу 5, иначеположить k=k+1 инайтимножество Г -1(k).

Шаг 4. В ерш инеk присвоить пометку l(k) по правилу

=	{	i + cik})	x(l	max	) k(l
иперейтик ш агу 3.	i Г −1 )(k
Ш аг 5. П оложить k=n, i=1, w(1)=n.
Ш аг 6. Д ля верш ины k	найти множество		Г (k).	И з всех верш ин
этого множествавыб рать такую	верш ину j, чтоб ы выполнялось				равенство

l(k)= l(j) + ckj . П оложить i = i + 1, w(i)=j.

Ш аг 7. Е слиk ¹ 1, то положить k=k-1 иперейтик ш агу 6, иначеостанов - массив w содержитверш ины, входящ иев критический путь, пометка конечнойверш ины - длинакритического пути.

Замечание: Задачисетевого планированияиуправления– это задачи, которыезаклю чаю тсяв определении последовательности операций, реализую щ ихнекоторый проект, и в распределении ресурсов между ними. В качестве критериев оптимальности рассматриваю тся минимизация времени выполненияпроекта, затрат, рискаи т.п. Д линакритического путив сети – это время, необ ходимоедляреализации всего проекта, араб оты (дуги), лежащ иенакритическом пути, об ладаю ттем свойством, что неимею трезервов, поэтому именно нанихследуетоб ратить вниманиепри планировании раб от. И зменениедлины критическойдугиведетк изменению критического времени.

Задач а о м аксим альном пот оке: пусть G= (X,U) - орграф б ез петель систочником s истоком t. И ст оч ником в орграфеG называетсяверш инаs, из которойдостижимы всеверш ины графа; ст ок t определяетсядвойственным об разом. К аждой дугесоответствуетчисло rij, котороеназываетсяпропускнойспособ ностью дуги. М ножество чисел{хij}, определенныхнадугах (xi,xj)ÎU, называю тпотокаминадугах, есливыполняю тсяследую щ иеусловияб аланса:

		ì v, еслиxi = s
а) å xij -		ï		= t ;
	å x ki = í- v, еслиx i
x:j j Г i ) (x	kx:k Г	−1 i ) (x ï	0, иначе
		î

б ) 0 < xij < rij длявсех( xi , xj )ÎU.

Задача о максимальном потоке заклю чается в нахождении такого множествапотоков по дугам, чтоб ы величинаv б ыламаксимальной. Реш е- ниеэтойзадачиосновано нат еор ем е [2, стр. 312]: величинамаксимального потокаиз s в t равнавеличинеминимального разреза < R*,`R* >, отделяю - щ его s отt. Разрез < R*,`R* > отделяетs отt , еслиs Î R*, t Î`R*. В еличиной такого разрезаназываетсясуммапропускныхспособ ностей всехдуг G, начальные верш ины которых лежатв R*, аконечные- в`R*, т.е.

		66	å
		= >			rij .	) * R *, Rv(
	<
					>R*,	R <) x, (x
		i	j	*

М инимальныйразрез - это разрез снаименьш им таким значением.

Э тазадачаи ее варианты могут возникать во многих практических приложениях, например при определении максимальной интенсивности транспортного потокамежду двумяпунктами накартедорог, представляемой графом. В этом примеререш ениезадачи о максимальном потокеукажеттакжету часть сети дорог, которая“насыщ ена” и об разует“узкоеместо” в отнош ении потокамежду двумя указанными концевыми пунктами. Д лянахожденияреш ениязадачи о максимальном потокеиспользуетсяал-

гор ит м Ф О РД А и Ф АЛ К ЕРС О НА:

Замечание: Д анный алгоритм основаннаприписывании верш инам графапометок, при этом верш инаможетнаходиться в одном из трех состояний:

∙верш инеприписанапометка, ионапросмотрена(т. е. онаимеет пометку

ивсесмежныеверш ины “об раб отаны”);

∙верш инаимеетпометку, но непросмотрена(т.е. невсесмежныесней верш ины “об раб отаны”);

∙верш инанеимеетпометки.

Пометкапроизвольной верш ины хi состоит из двух частей и имеет

одиниз двух видов [+хj ,δ] или[-хj , δ]. Ч асть +хj пометкипервого типаозначает, что поток допускаетувеличениевдоль дуги(хj , хi). Ч асть -хi пометки другого типаозначает, что поток можетб ыть уменьш енвдоль дуги (хj , хi). В об оихслучаяхδ задаетмаксимальную величину дополнительного потока, которыйможетпротекать по некоторому путиотs к хi .

Ш	аг 1. П рисвоить источнику s пометку [+s,∞].
Ш	аг 2. В ыб рать непросмотренную верш ину спометкой [ ± хk , θi ].

К аждой непомеченной верш ине хj Г (хi), для которой xij<rij, присвоить пометку [+хj , θj ], гдеθj=min{θi , rij - xij }. К аждой непомеченной верш ине

xj Г -1(xi), длякоторойxji >0, присвоить пометку [-xi ,θj ], где θj=min{θi , xji }. Ш аг 3. П овторять ш аг 2 до тех пор, пока либ о верш инаt неб удет

помеченаи тогдаперейти к ш агу 4, либ о t неб удетпомеченаи никаких других пометок нельзя б удетрасставить. Е сли при этом R* - множество помеченных верш ин, а `R* - множество непомеченных верш ин, то <R*,`R*> - минимальный разрез, асуммапропускныхспособ ностей надугахэтого разрезаесть величинамаксимального потокаv*.

Шаг 4. П усть верш инаt имеетпометку [ ± z ,θt ], тогдаположить x = t

иперейтик ш агу 5.

Шаг 5. Е слипометкав верш инехимеетвид [+y,θx ], то увеличить поток вдоль дуги(у,х) навеличину θt . Е слипометкав верш инехимеетвид [- y, θx ], то уменьш ить поток вдоль дуги(х,у) навеличину θt . П ерейтик ш агу

6.

67

Ш аг 6. Е сли y=s , то стереть всепометки и перейти к ш агу 1, иначе положить x=y иперейтик ш агу 5.

И звестными модификациями задачи о максимальном потокеявляю т-

ся:

а) Е сливместо одного источникаиодного стокарассмотреть несколько заданныхисточников и стоков, причем между различными источниками истокамипротекаю тпотокиразличныхпродуктов, то задачамаксимизации суммы всех потоков между источниками и стоками называется задачей о м н огопр одук т овом пот ок е. В этой задачепропускнаяспособ ность дуги являетсяограничением длясуммы всех потоков всех видов продуктов через эту дугу.

б ) Е сли рассмотреть граф, в котором выходной поток дуги равенее

входному потоку,		умноженному нанекоторое неотрицательное число, то
задачу о максимальном			потоке от s к t	называю т задачей о пот оках с
вы игр ы ш ам и.	В	такой	задаче потоки	могут и “ порождаться ” и
“поглощ аться”	самим графом, так что			поток, входящ ий в s, и поток,

выходящ ийиз t, могутизменятьсясоверш енно независимо.

Задач иразм ещения. В практическойдеятельностипостоянно возникаю тзадачи“наилучш его” размещ ениянекоторыхоб ъектов (об орудования, аварийныхслужб , телефонныхстанцийидр.). П риэтом, есликритерийоптимальностисостоитв минимизациирасстоянияотпунктаоб служиваниядо самой отдаленной верш ины графа, то задачи такого типаназываю тся м и- ним аксны м и задач ам и разм ещения. П олученныепри реш ении этихзадач местаразмещ енияпунктов об служиванияназываю тсяцентрамиграфа. Е сли критерий оптимальности состоит в минимизации суммы расстояний от верш инграфадо пунктаоб служивания (предполагается, что онединственен), то задачи такого типаназываю тся м инисум м ны м и задач ам и разм е- щения, аместаразмещ енияпунктов об служиванияназываю тсямедианами графа.

В ведем определения. Расстояни ем d(x,y) отверш ины хдо верш ины у называется длинакратчайш его пути из х в у. П ри х=у d(x,y)=0; при у R(x) d(x,y)=∞. В м атри церасстояни й (i,j)-ыйэлементравенрасстоянию

из верш ины хi	в верш ину хj; если жеиз хi в хj				нетпутей, то соответствую -
щ ийэлементполагаетсяравным ∞.
Рассмотрим граф G, длякоторого D - матрицарасстояний, V=(vj)n оп-
ределяетвесаверш ин. Ч исло S0(xi) называетсячи слом							внешнего разд еле-
ни я, если			{ ×		j ))}.i x,		x( d	v	max
	S0(xi) =	xi X		i
					{		))} x,	x( d	max
				xi X
Е сли vj	= 1, то величина l(xi) =					i j	называется экс-

центри си тетом верш ины х.

Ч исло St(xi) называетсячи слом внутреннего разд елени я, если

	68
	{	×
St(xi) = xi X
В ерш инахо*, длякоторой		{ 0
So(хо*)=	xi X
называетсявнешни м центром граф а.
В ерш инахt*, длякоторой	{ t
St(хt*) =
	xi X

i j))}.i x,	x( d v	min
i )}x( S	min

i )} x( S min

называетсявнутренни м центром граф а.

В ерш инах*, для которой

l(х*) =	{	i )}x(l	min
называетсяцентром графа.	xi X

Ч исло внеш него разделенияхо*, являю щ еесявнеш ним центром, называетсявнешни м рад и усом ρо = Sо(хо*). Ч исло внутреннего разделенияхt*, являю щ ееся внутренним центром, называется внутренни м рад и усом ρt = St(хt*). Е сли граф имеетцентр х*, то эксцентриситетl(х*) называется ра-

д и усом графа.

Замечание. Е сли конечный граф G = ( X, Г ) являетсяполным, то его

радиус ρ ≤ 2 , авсякаяверш инахо , длякоторой

| Г (хо) \ { хо} | = max

Г

}x{\ )(x

служитцентром.

x X

Т очкауo*, длякоторой

{

×

)} x, y( d

v

max

min

So(уo*) = y G xi X

i

i

,

называетсяабсолютным внешни м центром

графа.

Т очкауt*, длякоторой

{

×

)}y, x( d

v

max

min

St(уt*) = y G xi X

i

i

,

называетсяабсолютным внутренни м

центром

графа.

Ч исло внеш него разделенияаб солю тного внеш него центраназывается

абсолютным внешни м рад и усом ro = So(yo*). Ч исло внутреннего разделе-

нияаб солю тного внутреннего центраназываетсяабсолютным внутренни м

рад и усом rt = St(yt*).

Ч исло σо(xi)

называетсявнешни м перед аточным чи слом , если

σо(xi) =

å{

×

i j ))}i x,v x( d

xi X

.

Ч исло σt(xi)

называется внутренни м

перед аточным

чи слом , если

σt(xi) =

å{ ×

i j ))}i x,v x( d

x X xjX

.

j

69		{σ			)} x(	min
В ерш ина`хо , длякоторой σо(`xo ) = xi X			0	i	называется внеш-
ней м ед и аной графа.	{σ			)} x(		min
В ерш ина`хt , длякоторойσt(`xt ) = xi X
		t	i	называетсявнутрен-

ней м ед и аной графа.

П ри м ер. П усть граф G заданматрицейрасстоянийD(G), всевесаvj и cij примем равными 1. В ычислим внеш ниеивнутренниепередаточныечиславерш ин. Э ти числаприведены в присоединенных к матрицерасстояний строкеи столб це. П о полученным передаточным числам видно, что внеш - неймедианой являетсях5 сσ0(х5) = 7 ичто сущ ествую ттривнутренниемедианы х2, х3 их5, каждаясвнутренним передаточным числом, равным 9.

			х1	х2	х3	х4	х5		х6	σ0(хi)
		х1	0	1	2	3	2		3	11
		х2	3	0	1	2	1		2	9
D(G) =		х3	4	3	0	1	2		3	13
		х4	3	2	2	0	1		2	10
		х5	2	1	1	2	0		1	7*
		х6	1	2	3	4	3		0	13
		σt(хi) 13		9*	9*	12	9*		11
		ЗА Д А Ч И И У П РА Ж Н Е Н И Я

1.И спользуя алгоритм Д ейкстры, найти кратчайш ий путь из s в t в графах, изоб раженныхнарис.1.

2.И спользуя алгоритм Д ейкстры, определить кратчайш ие путииз

верш ины 1 в каждую другую	верш ину награфе, изоб раженном на рис.2.
П редположим, что послеэтого об наружилось, что дуга(4,2) длиной1
считалась отсутствую щ ей. М	ожно ли при этом воспользоватьсяужеполу-

ченными результатами илинеоб ходимо вновь в полном об ъемепроизвести вычисления?

G 1

G2

G 3

G4

Рис.1

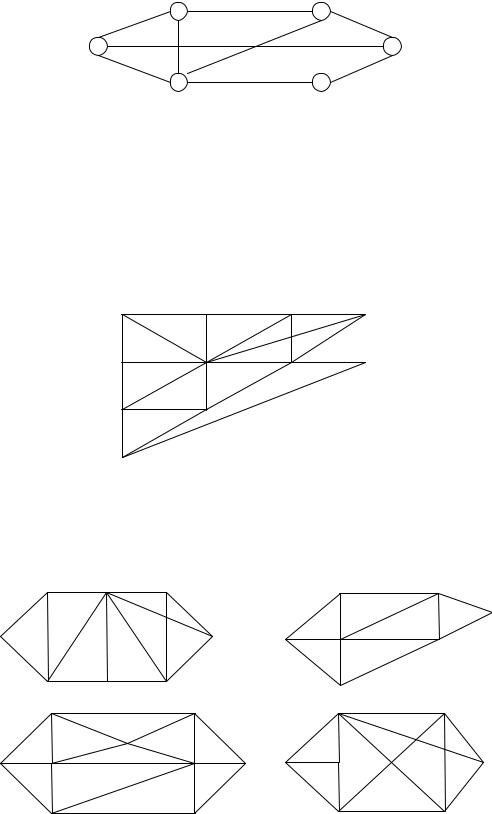
	70
2	3
1	6
4	5

Рис.2 3. У правляю щ ийгостиницейдолжензаб ронировать номерадляново-

б рачныхнаследую щ иймесяц. О нполучилопределенноеколичество заявок наб ронированиесразличными датами приездаи отъезда. К аждоевозможноеб ронированиеномеров даетгостиницеопределенный доход, в зависимостиоттого, кем являю тсяклиенты. К аким об разом в этом случаеиспользовать алгоритм Д ейкстры длявыраб отки расписанияб ронированияномеров, приносящ его гостиницемаксимальныйдоход?

4. В графеG, изоб раженном нарис.3, найтипуть сминимальным числом дуг из хв у, если а) х=х11, у=х1; б ) х=х1, у=х8; в) х=х6, у=х11.

G

Рис.3

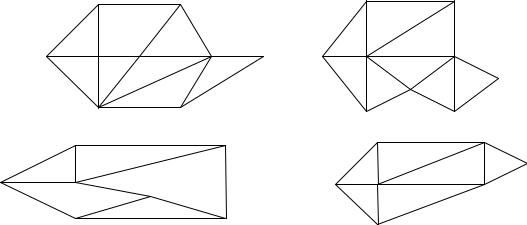
5.Н айтимаксимальныйпуть из s в t в графах, изоб раженныхнарис.4.

6.Строительнаяфирмаподписалаконтрактнастроительство нового

спортзаладля колледжа. В контрактепредусмотрены б ольш иеш трафы за невыполнениераб оты в срок, поэтому дляруководителяфирмы важно выяснить, какиестроительно-монтажныераб оты имею треш аю щ еевлияниена

G 1

G2

G 3	G4
Рис.4